23.9: Questions
- Page ID
- 32713
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Quick questions
You should be able to answer these questions without too much difficulty after studying this TLP. If not, then you should go through it again!
What type of stress-strain curve does a normal arterial wall show?
- Answer
-
C
What type of stress-strain curve does natural rubber show?
- Answer
-
B
What type of stress-strain curve do metals at small extensions show?
- Answer
-
A
What type of stress-strain curve does bone show?
- Answer
-
A
What type of stress-strain curve does skin show?
- Answer
-
C
Deeper questions
The following questions require some thought and reaching the answer may require you to think beyond the contents of this TLP.
- Estimate the coefficient of restitution (sometimes known as the resilience) of a human hair using the hysteresis curve below:
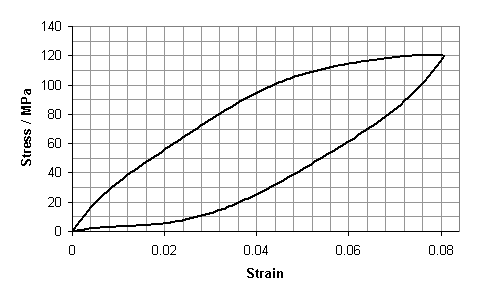
- Answer
-
The area under the loading curve is the work done per unit volume of the stressed material, which is equal to about 166 squares.
The area under the unloading curve is the recovered work, which is equal to about 72 squares.
The coefficient of restitution is therefore found by dividing the area under the unloading curve by the area under the loading curve, giving an answer of about 43%.
Why are hairs used in violin bows?
- Answer
-
Hairs are used in violin bows because this low resilience enables the damping of resonances. The desired resonances are in the violin strings!
A fly of mass 30 mg hits a spider's web at 0.8 m s-1 and is stopped by two capture threads each of diameter 0.7 micrometres and length 5 cm. Calculate the maximum tensile strain in the threads, assuming that the tensile loading curve of the capture threads can be approximated as a straight line with gradient 0.1 GPa.
Hint: Consider the kinetic energy of the fly and the work done in extending the capture threads.
- Answer
-
If the tensile loading curve is linear, then the work done in extending a thread, which is equal to the area under the curve, can be calculated using 0.5 x load x extension, or 0.5 x stress x strain, or 0.5 x Young's modulus x strain2
At 0.8 m s-1, the kinetic energy of the fly is equal to ½mv2
= 9.6 x 10-6 J.
The total volume of the two threads
= 2 x 0.05 x π(0.35 x 10-6)2
= 3.85 x 10-14 m3Work done per unit volume of thread
= 9.6 x 10-6/3.85 x 10-14
= 2.49 x 108 J m-3
= ½Eε2Using the fact that E = 0.1 GPa, ε = 2.23
(.. continuation from previous question) Given that the coefficient of restitution of a capture thread is 35%, calculate the total energy dissipated in the two threads.
- Answer
-
The energy dissipated is 65% of the kinetic energy of the fly = 6.24 x 10-6 J
(.. continuation from previous question) Since the threads are very thin, this energy would easily be dissipated as heat to the surrounding air. However, supposing that the process is adiabatic (no heat transfer occurs), estimate the temperature rise that would occur. The density of viscid silk is 1500 kg m-3 and the specific heat capacity is 1400 J K-1 kg-1.
- Answer
-
The total heat capacity of both threads
= total volume x density x heat capacity
= 3.85 x 10-14 x 1500 x 1400 = 8.09 x 10-8 J K-1The adiabatic temperature rise would be
= energy/heat capacity
= 6.24 x 10-6/8.0 x 10-8
= 65 K
(.. continuation from previous question) Comment on the effects of using cables with a large diameter made of viscid silk, for example to decelerate aircraft landing on carriers.
- Answer
-
Thick cables made of viscid silk would be unable to dissipate the heat quickly to the surroundings, and very large temperature rises would be seen.


