32.3: Theory 2
- Page ID
- 33012
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The formation of glasses can be understood from both a kinetic approach and a thermodynamic approach. In this section we will review both.
Kinetic Approach to Glasses
Consider a polymeric liquid being cooled towards its melting temperature. Once the temperature of the liquid reaches Tm the solid crystalline phase is thermodynamically favourable. In order for the liquid to undergo a phase transition to the solid state a two-step process must take place:
- Nucleation of solid seeds
- Growth of the seeds
Nucleation is the formation of small crystalline solid particles in the liquid. As a result a new interface is formed in between the solid particle and the liquid. This interface has an associated energy, the interfacial energy. For a successful nucleation event to occur the polymer must find extra energy from somewhere to "pay" for the energy cost of creating a new interface.
This energy is called the "driving force" for nucleation. As we cool the liquid just below Tm we see no nucleation at first. Instead nucleation occurs at a temperature T< Tm, below the expected temperature. When the polymer is still liquid below Tm it is said to be undercooled. The amount of "undercooling" is limited by the nucleation rate.
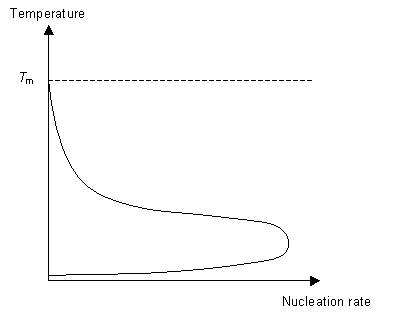
The second stage of the phase transition is the growth of the nucleated seeds. This is a thermally activated process, which means that its rate is dependent on the temperature. So for fast crystal growth the ideal method is to cool the polymer to just above Tg to allow for nucleation to occur and then raise the temperature to just below Tm to allow growth to occur.
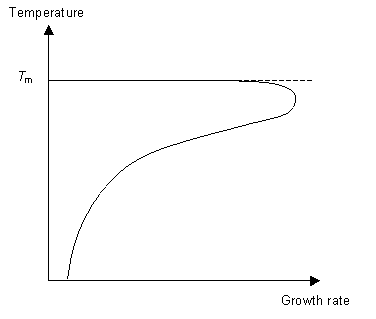
Understanding these concepts we can now think about how best to cool a liquid in order to form a glass. To ensure we form a glass we want to reduce the number of nucleation events as much as possible (otherwise we will have crystals not an amorphous solid) and not allow growth to occur. By cooling the liquid very quickly (i.e. quenching it) it is possible to reduce the mobility of the molecules to the point where they can not move around to order themselves periodically as they do not have the energy to diffuse far enough. This concept can be expressed on a TTT (time temperature transformation) graph.
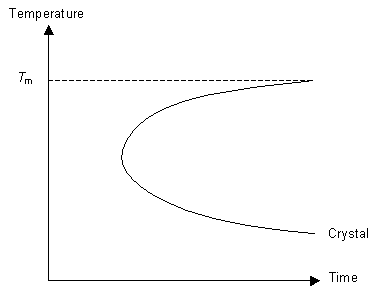
The graph represents the degree of crystallinity of the polymer as it is cooled. The line marked "crystal" indicates a specific degree of crystallinity (for example it may indicate 90% crystallinity in the sample). The TTT graph is used for isothermal transformations, but here it is loosely applied to continuous cooling.
If the cooling rate is fast enough then the polymer can be cooled so that it does not enter the crystal region of the graph. In this case, although the polymer is below Tm, it does not crystallise because the molecules can not move to order themselves periodically (as in a crystal). Instead the polymer has formed an amorphous solid, or a glass.
Thermodynamic Approach to Glasses
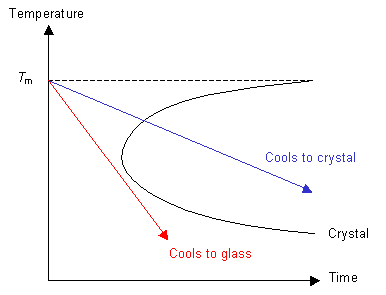
Consider the red line from the graph above. Above Tm the polymer is a liquid. At temperatures a long way below Tm the polymer behaves like a solid, although it is not crystalline. In this state the glass has the properties of a solid, but may exhibit aspects of liquid behaviour over long time scales.
(There is a common misconception that inorganic glasses behave in this same way. This liquid behaviour is incorrectly thought to be responsible for the windows of old buildings often being thicker at the bottom than at the top. This is discussed briefly, with citations, for those who are interested on a separate page in this TLP.)
Have a look at the graph of the polymer's enthalpy at different temperatures:
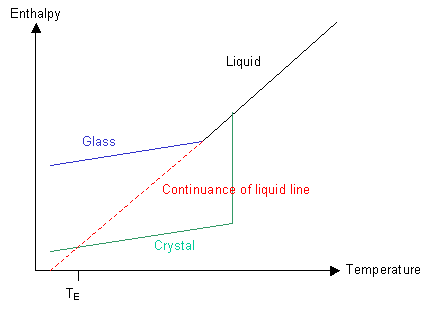
If nucleation can occur and the rate of cooling is not too high, then the green line will be followed and the polymer will crystallise below Tm to form a crystalline solid.
If the polymer is quenched so that ordering of the molecules cannot take place then the blue line will be followed and the polymer will form a glass below Tm.
Let us now imagine what would happen if we could follow the red line and keep cooling the liquid without forming a crystalline solid. There is a point, TE, at which the enthalpy of the supercooled liquid falls below that of the crystalline solid. Similarly, there is a temperature, TK, the Kauzmann temperature, below which the entropy of the liquid would be less than that of the corresponding solid. In other words, below the Kauzmann temperature the liquid should be more ordered than the corresponding solid. As we know, solids are highly ordered and liquids are not, so the liquid cannot reach this condition.
The paradox is avoided because by the time the Kauzmann temperature has been reached on cooling, the liquid has gone through transition into a glassy state.
Important points relating to phase transitions within polymers
- Glass formation can be explained both kinetically and thermodynamically
- Glasses can be formed by quenching (rapidly cooling) the polymer so that the molecules do not have time to order themselves into a periodic crystal
- Glasses exhibit the properties of a solid, but over long time scales can flow like a liquid
- Below the Kauzmann temperature the polymer must either be a crystalline solid or a glass as the liquid phase is thermodynamically unstable


