33.4: Angle of Repose

When a container full of granular matter is poured onto a flat horizontal surface from a point source such as a funnel, it will form a conical pile of material. This conical pile will have a characteristic angle of repose, or equivalently, slope of repose. The angle of repose is the angle between the horizontal surface and the sloping surface of the pile. The tangent of this angle is the slope of repose.

https://www.doitpoms.ac.uk/tlplib/gr...deos/large.mp4

https://www.doitpoms.ac.uk/tlplib/gr...deos/small.mp4

It is found experimentally that the angle of repose is determined by a number of factors. One obvious factor is friction, and a second is cohesion caused by the presence of liquid bridges between granules which enable the granules to stick together.

Simple experiments with screw-top glass bottles half-full of fine grain loose sand are able to show various aspects of the flow behaviour of granular materials. In the videos below there are two bottles of sand, one half-full of sand and half-full of air, and the second half-full of sand and half-full of water.

If, to begin, both bottles are rolled slowly on their sides on a horizontal table, the sand in both bottles will move to form packings of the granules with flat horizontal surfaces.

If the bottle half-full of sand and half-full of air is tilted to stand on its end, it can be seen that the sand will form a slope with a particular angle of repose. If the bottle is further tilted in the same direction, the assembly of granules on the slope will be seen to flow in such a way that the individual granules rotate as they flow down the slope, rather than slide down the slope in order to maintain the angle of repose.

If the bottle half-full of sand and half-full of water is tilted to stand on its end, the outcome depends on the timescale over which the tilt occurs.

If the timescale is short, e.g., less than a second, the surface of the sand is disrupted in such a way that the granules pack down eventually to a horizontal surface so that the surface behaves as though it is a liquid.

If the tilt occurs gradually, e.g., over a period of a few seconds, it can be seen that the slope attained by the sand when the bottled is tilted to stand on its end is the same within experimental error as the bottle half-full of sand and half-full of water. If the bottle is further tilted slowly, the assembly of granules on the slope behaves as they do in air.

In clays such as London clay consolidated over some 50 million years (en.Wikipedia.org/wiki/London_Clay), large lumps of sheared blocks of clay known as ‘greasy-backs’ can fall from faces of tunnels during excavation. The bottom surfaces of these sheared blocks consists of regions of soil where local expansion has occurred and where the failure process on shearing is a consequence of the rotation of granules in these regions, as if they were tumbling down an angle of repose, rather than the translation of the granules. Examination of the surfaces of these greasy-backs after failure shows that they have the characteristics of plasticised clay paste resembling heavy engine grease (C.N.P. Mackenzie, Traditional Timbering in Soft Ground Tunnelling: A Historical Review, British Tunnelling Society, 2014).

Predictions of the angle of repose

Predicting the angle of repose for a particular family of granules is not straightforward: most angles of repose are acquired from experimental measurements, such as those quoted in the Wikipedia entry on ‘Angle of repose’ (en.Wikipedia.org/wiki/Angle_of_repose). For many granular materials a typical angle of repose will be between 25° and 40°.

For smooth spherical particles all of the same size, a very simple model can be used to appreciate how the packing of spheres in three dimensions has consequences for the stability of slopes. Suppose three identical spherical particles on a slope of angle θ relative to the horizontal pack together so that they form the base of a regular tetrahedron if a fourth identical sphere is added on top of these three particles. Depending on the orientation φ of the base of the tetrahedron with respect to the slope, the tetrahedron will be stable if the angle θ is increased from zero (when the particles are on a horizontal base) to a critical angle θ_c at which the fourth sphere rolls away down the slope from the three identical spheres (all presumed to be (just) held by friction on the slope at this angle).

At a particular angle of φ and θ, simple geometry shows that the top sphere is only stable if the vector defining the gravitational force points through the projection of a suitable base triangle on the horizontal plane. The corners of this base triangle are defined by the positions of the centres of mass of the three identical spheres on the base of the tetrahedron.

For a particular φ, the maximum angle of stability for this geometry is

\[ \theta_c = arctan \frac{1}{2 sqrt{2} cos({60 ^{\circ} - \varphi}}) \]

A proof of this formula is given here.

Hence, when φ = 0°, when one of the corners of the base triangle is at the lowest point on the slope θ_c = 35.26°, and when φ = 60°, when one of the sides of the base triangle is at the lowest point in the slope, θ_c = 19.47°.

A graph of θ_c as a function of φ is shown below.

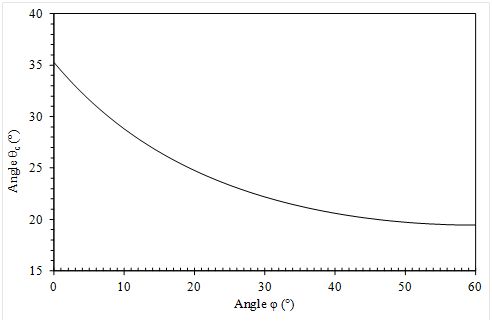
If it is assumed that the orientation of bases of such tetrahedra are random on a pile of granular matter, then the observed angle of repose for smooth non-cohesive particles can be argued to be the average value of θ_c over the interval 0° < φ < 60°, i.e., 23.8°, determined numerically using Simpson’s rule or the Trapezium rule. This equates to an effective coefficient of friction of tan θ_c of 0.44.