33.6: Yielding of Disturbed Saturated Soils in Triaxial Stress Tests
- Page ID
- 33027
A schematic yield surface ABCDEFG of a soil plotted as a function of two parameters: η and vλ is shown in the diagram below.
The vertical axis is η, the stress obliquity, defined as q/p', where in a triaxial test on a cylinder of soil, q is the axial compressive stress, σa, minus the radial compressive stress, σr, and p' is the mean total compressive stress, p, minus the pore water pressure, u. p' is also known as the mean effective compressive stress. It is useful to note that the effective axial and compressive stresses are σa' = σa − u and σr' = σr − u respectively, and that
\[ q = \sigma_a - \sigma_r \]
and
\[ p' = \frac{\sigma_a + 2 \sigma_r}{3} - u \]
The convention in soil mechanics is to take compressive stresses as positive quantities. This is an important difference from the convention used in the TLP Stress Analysis and Mohr's Circle.
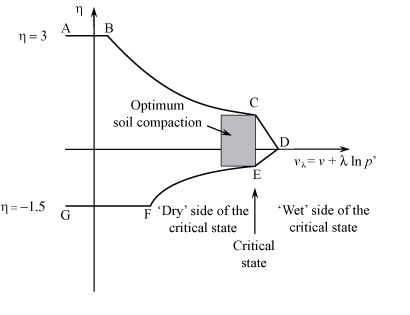
The horizontal parameter vλ is a linear function of the specific volume, v, and the logarithm of the mean effective compressive stress, p'. The specific volume is the ratio of the volume occupied by soil to that which it would occupy if the voids were eliminated. Therefore, values of v of 2 are typical for soils.
We now need to define what we mean by the 'Dry' side of the critical state and the 'Wet' side of the critical state for soils. 'Wet' means that when you shear the soil, grains expel water so that the soil feels sticky to the touch. 'Dry' does not literally mean dry: it means the pores are full of water, but when you shear the soil, the grains ride over one another - this is called dilation. The void space increases and fluid is taken into the soil. Remoulding the soil in your hands will dry your hands. At the critical state, the soil neither dries your hands nor feels sticky to the touch.
For soils at the critical states C and E in the above diagram and soils on the 'wet' side of C and E, it is found experimentally that there is a linear relationship between the specific volume of the soil aggregate, v, occupied by the soil and the logarithm of the mean effective compressive stress. Hence, a graph of v against ln p' for such soils is experimentally found to fit an equation of the form
\[v = v_{\lambda} - \lambda ln p' \]
where by convention p' is usually normalised with respect to a standard stress of 1 kPa. Micromechanically, such an equation in v − ln p' space can be rationalised in terms of particle breakage as p' increases in crushable aggregates, and the fractal nature of the process of breakage in such aggregates, in which the tensile strength of the smallest particles within an assembly of particles constituting an aggregate of soil grains determines the yield stress of the aggregate (G.R. McDowell and M.D. Bolton, ‘On the micromechanics of crushable aggregates’, Géotechnique 48, 667-679 (1998)).
Physically, it can be appreciated that mud saturated with water has a high v relative to the same mud with water squeezed out of it as a consequence of an increase in p', and that there will be a lower asymptotic limit of v achieved by mud at large mean effective compressive stresses with the water squeezed out. Schematically, we might imagine the following:
Each part of this yield surface in (vλ, η) space will now be explained in more detail, going clockwise around the yield surface, starting with A and finishing with G:
Line AB
When σa >> σr, η → 3, as σr/σa → 0. Under these circumstances, axial compression will cause a test cylinder of soil to split on axial planes, just as logs split for firewood. Open cracks are therefore produced in this part of (vλ, η) space.
Curve BC
In this region of (vλ, η) space the Mohr-Coulomb failure criterion is assumed to hold:
\[ \tau = \tau* + \sigma'_n tan \phi ' \]
where in this equation the compressive stress σ′n is taken here to be positive using the conventions of soil mechanics, and where the dash denotes that pore water pressure has been taken into account, so that σ′n is an effective normal compressive stress.
This criterion is discussed further on the TLP page https://www.doitpoms.ac.uk/tlplib/metal-forming-1/yield_non_metals.php .
For the interpretation of this criterion for triaxial stress tests on soils using the convention that in soil mechanics, pressures are taken to be positive, it is reasonable to map Mohr-Coulomb behaviour in (τ,σ′n ) space onto (q, p') space so that a graph of q against p' is taken to be of the form

\[ q = q_0 + mp' \]
A model for why this is reasonable is shown here.
There are a number of caveats in making the assumption that the Mohr-Coulomb behaviour holds. The most important caveat is that the Mohr-Coulomb criterion does not have a physical base – it is an empirical equation based on the interpretation of experimental observations. In addition, in the Mohr-Coulomb yield criterion the intermediate principal stress is not required, whereas it clearly is required for the interpretation of triaxial stress tests.
Notwithstanding these caveats, rearranging (1), we have:
\[ \eta = \frac{q}{p'} = \frac{q_0}{p'} + m \]
If we now define ln p' to be x, then p' = ex, and so (2) can be rearranged in the form
\[ \eta = q_0 e^{-x} + m \]
Hence, a graph of η against x has a gradient of −q0e−x, so that the gradient is negative, decreasing in magnitude exponentially as x increases. Hence plotting η against v + λ the Mohr-Coulomb yield criterion has the same form, since v is taken to be a constant and λ is a dimensionless constant.
Eventually, as ln p' increases while η decreases, a critical state C is reached where physically the soil is sufficiently loosely packed that there is no specific volume change during a triaxial stress test, i.e., the soil neither contracts nor dilates. Hence, there is a critical value of vλ at C. This critical value of vλ is given the symbol Γ.
During both clockwise and anticlockwise shearing, soils dilate for vλ < Γ, i.e., on the dry side of critical and contract for vλ > Γ, i.e., on the wet side of critical.
Line CD
Line CD represents the behaviour of soft soil during plastic yielding and flow at C, and on the wet side of the critical state C, through the Original Cam-Clay model. The proof that CD is a straight line can be found here. As shown here, C is defined by a point (Γ, M) in (vλ, η) space, while, as will also be shown below, D is defined by a point (Γ + λ - κ, 0).
In (vλ, η) space, CD is the straight line
\[ (\lambda - \kappa) \eta = M v_{\lambda} - M (\Gamma + \lambda - \kappa) \]
It is useful to have an idea of the values of some of the parameters in this model. For a material like London Clay, M = 0.89, λ = 0.161, κ = 0.062 and Γ is 2.759 when p'C is 1 kPa (A. Schofield, Disturbed Soil Properties and Geotechnical Design, Thomas Telford Ltd., London, 2005, p. 100).
Line DE
Line DE is the equivalent of line CD, i.e., Original Cam Clay yield behaviour but for when η < 0, i.e., for when σa << σr. The critical state E occurs at a position (Γ, ME) in (vλ, η) space where there is no physical reason for ME and M to be the same.
Curve EF
Line EF is the equivalent of curve BC, i.e., the yield surface is defined by Mohr-Coulomb failure, but under circumstances where η < 0. At F a stress state is reached where σa/σr = 0.
Line FG
When σa << σr, η → −1.5 is reached as σa/σr → 0. Under these circumstances, radial compression causes cracking in planes perpendicular to the axis of a test cylinder: it can crack into many discs. This is termed spalling – it has the same nomenclature as that used to describe the failure in compression of thin films on substrates because of failure due to in-plane biaxial compressive stresses.
Finally, note that F and B occur at different values of vλ: spalling occurs over a larger range of mean normal effective pressures than its equivalent process of cracking when σa >> σr.


