12.4: Phase Diagrams
- Page ID
- 8244
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Free energy curves can be used to determine the most stable state for a system, i.e. the phase or phase mixture with the lowest free energy for a given temperature and composition. Below is a schematic free-energy curve for the solid phase of an alloy.
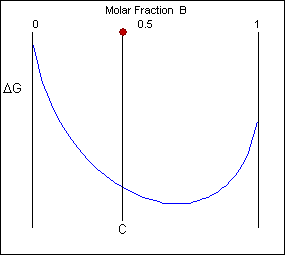
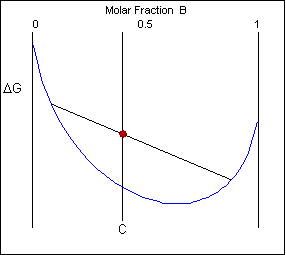
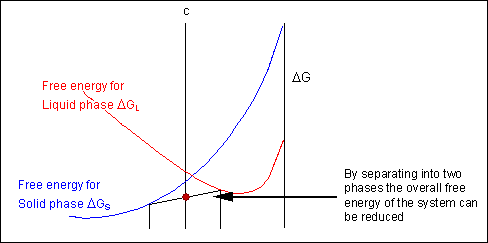
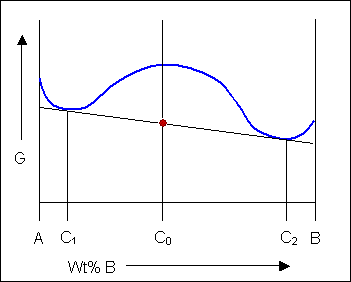
The solid shown could either exist as a mixture or as a homogeneous solution of A and B. The figures below show that an alloy of composition C can exist in different configurations with differing free energies. In the first figure (below) the free energy of unmixed A and B is shown as the diagonal black line. The free energy of this mixture at composition C is shown as a red point.

The system can reduce its free energy by existing as a mixture of two phases
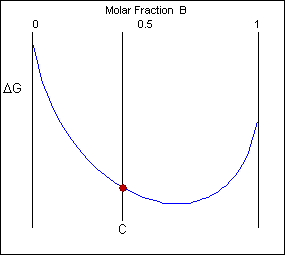
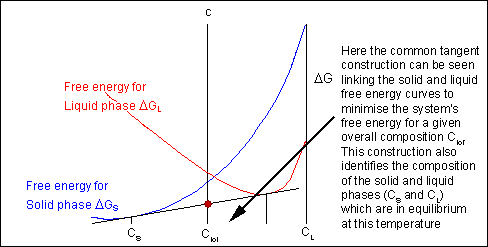
Though the system has reduced its free energy from that of the mixture, the most stable configuration for the system is a solid solution. This allows the free energy of the system to sit on the free energy curve.
For most systems there will be more than one phase and associated free-energy curve to consider. At a given temperature the most stable phase for a system can vary with composition. While the system could consist entirely of the phase which is most stable at a given composition and temperature, if the free energy curves for the two phases cross, the most stable configuration may be a mixture of two phases with compositions differing from that of the overall system. The total free energy of the system in any given two-phase configuration can be found by linking the two phases in question with a straight line on a free-energy plot.
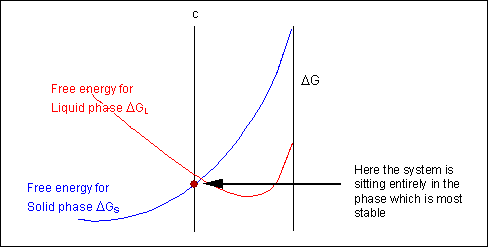
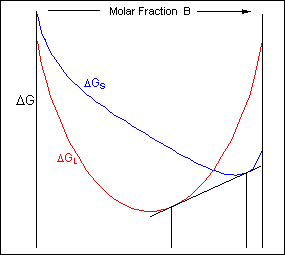
Taking a line that is a common tangent to the two free-energy curves produces the lowest possible free energy for the system as a whole. Where the line meets the free energy curves defines the composition of each phase.
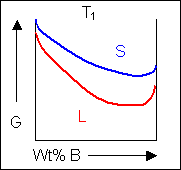
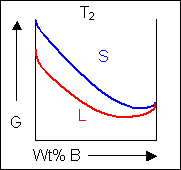
For positions where it is not possible to draw a common tangent between the two free-energy curves the system will sit entirely in the phase with the lowest free energy. The borders between the single- and two-phase regions mark the positions of the solidus and liquidus on the phase diagram.
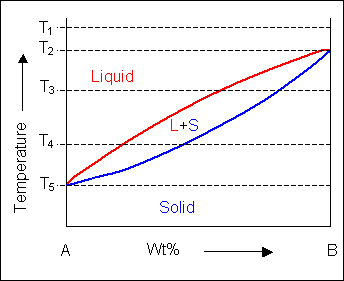
When the temperature is altered the compositions of the solid and liquid in equilibrium change and build up the shape of the solidus and liquidus curves on a phase diagram.
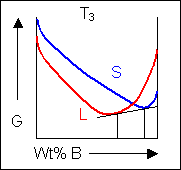
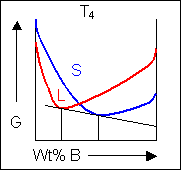
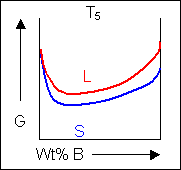
Below, a binary system can be seen along with the free-energy curves for the liquid and solid phases at a range of temperatures shown on the phase diagram.
 |
 |
|
 |
||
 |
 |
 |
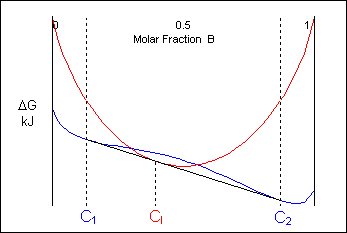
The free-energy curves and phase diagrams discussed in Phase Diagrams 1 were all for systems where the solid exists as a solution at all compositions and temperatures. In most real systems this is not the case. This is due to a positive ΔHmix caused by unfavourable interactions between unlike neighbour atoms. As the temperature is reduced the ΔHmix term becomes more significant and the curve turns upward at intermediate compositions, resulting in a curve with two minima and one maximum as described earlier. A common tangent can then be drawn between the two minima showing that the system can reduce its free energy through existing as a mixture of two distinct phases.
The free energy of a system of composition Co can be minimised by existing as a mixture of two solid phases of composition C1 and C2:
This effect can result in a system which, though single-phase upon solidification, will separate into two solid phases on cooling (e.g. Cr-W).
Another possible result is that the free-energy curve for the liquid will intersect the up turned section of the free-energy curve for the solid before the temperature is high enough to induce the formation of a solid solution. As the temperature is increased, the free-energy curve for the liquid moves downward relative to the solid curve and reaches a position where it is possible to link two parts of the solid free energy curve and one part of the liquid free energy curve with a common tangent. At this temperature three phases are in equilibrium.
Here the system is at the eutectic temperature and three phases can be joined by a common tangent:
This is known as the eutectic temperature. At this temperature there will be a composition which solidifies at a single temperature through the co-operative growth of the two solid phases. This is the eutectic composition. It is this composition which will exhibit the lowest melting point for the system.
At temperatures above that of the eutectic there will be two common tangents producing two two-phase regions at the same temperature. The two different solid phases are commonly labeled as α and β
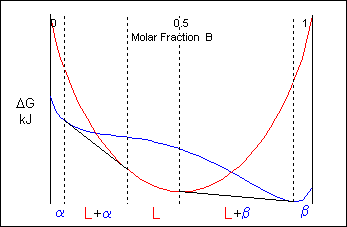
Eutectic systems therefore have a liquidus which contains a V to the eutectic point where it meets the eutectic invariant-reaction line.
Here is an example of a eutectic phase diagram. α and β are both solid phases.
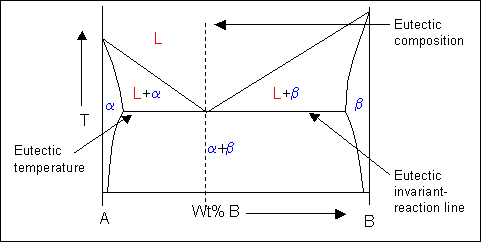
The two-phase solid region on the phase diagram will consist of a mixture of eutectic and either α or β phase depending on the whether the alloy composition is hypoeutectic or hypereutectic. The constitution of an alloy under equilibrium conditions can be found from its phase diagram. This will be discussed in a later section.


