21.2: What Metals can be Recycled
- Page ID
- 43528
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In short, almost all metals can. For example in the U.S., of the 132 million tonnes of metal ‘apparent’ supply, recycling contributed 67 million tonnes. That’s equivalent to about 50.8% [1]. In the UK, iron and steel make up the majority of the recycled metal in use. It is supplied mainly from industry and increasingly from municipal and household waste. Common examples include aluminium and tin/steel cans, and cars.
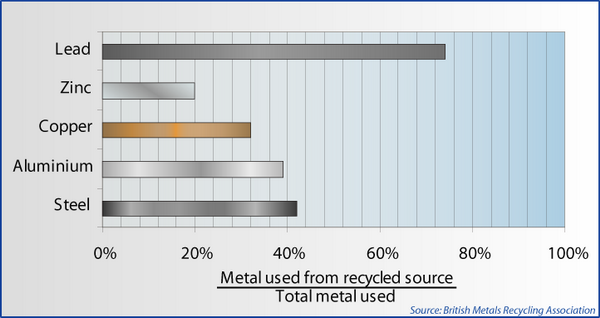
UK metals recycling statistics [2].
However, the process of metal recycling is not as simple as ‘melt it’, materials science knowledge is needed. There are two viewpoints to the recycling process, the recycling of individual metals, and the recycling of whole products.
Is recycling economically feasible?
Recycling is a great idea, in theory. The sad fact is that unless there are clear economic gains from recycling metal, large-scale initiatives are unlikely to become popular. To be economically viable, the energy saved by recycling needs to be significantly larger than the energy needed to produce the metals from ores.
There are statistics quoted for the amount of energy saved by recycling, for example these from the British Metals Recycling Association [2]:
|
Metal
|
Energy Saving (%)
|
|---|---|
|
Steel
|
62 - 74
|
|
Copper
|
87
|
|
Zinc
|
63
|
|
Lead
|
60
|
But, where do these numbers come from?
It is the job of the materials scientist to come up with values like the ones above, requiring calculation as precisely as possible using fundamental background knowledge.
Aluminium Production: An Example Calculation of the Energy Saved by Recycling
To find how much energy is saved by recycling aluminium, the amount of energy expended in primary production has to be calculated. When this is known, it can be compared with the energy expended to recycle the same amount of aluminium. 1 kg is a standard mass that will be used in this calculation to compare the two energy values.
Primary Production of Aluminium
The Bayer - Hall-Héroult process produces primary aluminium from bauxite ore. Initially, the Bayer process produces pure alumina (Al2O3) by dissolving the raw bauxite ore in aqueous alkali solution. This is carried out at high pressure and temperature. Pure Al(OH)3 is precipitated from the resulting solution, which allows separation of insoluble impurities. It is then calcined to pure alumina.
Next, the Hall-Héroult process involves an electrochemical cell and pure Al2O3 as the feed material. It is dissolved in a molten Cryolite electrolyte (Na3AlF6 – itself modified by the addition of AlF3, CaF2 and others) which brings the melting temperature to 950–1000°C. The addition of the cryolite therefore saves energy.
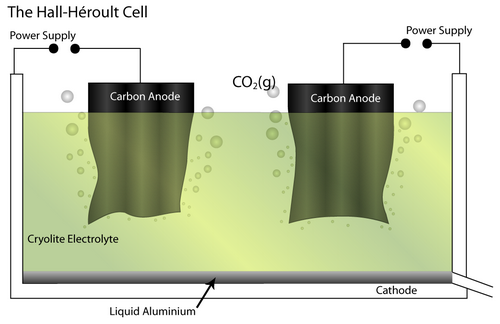
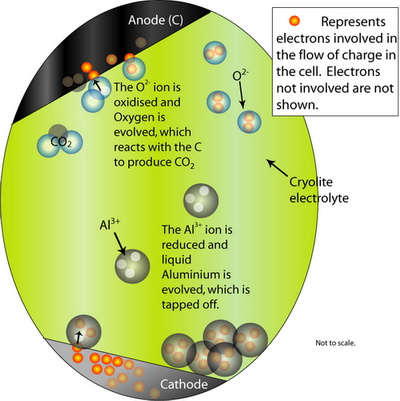
At the cathode, the Al2O3 is reduced to molten Al. At the anode, oxygen from the alumina reacts with the C electrode to form CO2(g).
The overall cell reaction is written as:
\[Al_2O_3(l) + \frac{3}{2}C \rightarrow 2 Al(l) + \frac{3}{2}CO_2 (g)\]
\[\Delta G (1273 K) = 686 \text{ kJ} \text{ at } ~ 975 ^{\circ} C\]
(ΔG for this reaction can be found using the Ellingham diagram.)
 -->
-->
The minimum reversible standard potential E0 is given by:
\[E^{\circ} = -\frac{\Delta G ^\circ}{6F}\]
where G is the Faraday’s constant.
\[E^{o}=\frac{686000}{6 \times 96500}=-1.18 \mathrm{~V}\]
As the Al2O3 is decomposed, it will decrease in concentration in the cryolite solution. This will cause the activity of the Alumina (\(a_{Al_2O_3}\)) to decrease until saturation of the solution with Al2O3 is restored. The decrease in the value of \(a_{Al_2O_3}\) affects the reversible potential (causes it to increase in magnitude from the standard potential) because of the Nernst equation (the derivation of which is given here [5]).
\[E_{r e v}=\frac{R T}{6 F} \ln a_{A l_{2} O_{3}}\]
The symbol Erev represents the minimum potential required that has to be overcome to start producing any Al at the cathode. The actual potential required is much higher than just the value of Erev, due to factors such as polarisation and Ohmic losses. So, the final potential required for the Hall-Héroult cell (Ecell) is given by:
\[E_{cell}=\left|E_{r e v}\right|+\eta_{A}+\eta_{C}+I \cdot R\]
where the symbols ηA and ηC refer to overpotentials at the anode (A) and cathode (C), respectively. Typically, ηA ≈ 0.5V and ηC ≈ 0.5V. I·R is the Ohmic loss. Most of the resistance, R, (>80%) in this value arises in the molten electrolyte. I·R ≈ 2.5 V at a typical current density of I ≈ 1 A cm-2 and a capacity rating of 100 kA. (These cells are designed to operate in the range 50–250 kA.)
Under the above conditions, Ecell ≈ 5V.
Now the energy can be found by first applying Faraday’s law (The mass of an element discharged at an electrode is directly proportional to the amount of electrical charge Q passed through the electrode) to the value of Ecell to calculate the amount of charge (Q) that is required to produce 1 kg of Aluminium:
\[Q=\frac{3 F}{\left(\frac{M_{A l}}{1 k g \times 10^{3} g k g^{-1}}\right)}=\frac{3 \times 96540}{\left(\frac{27}{10^{2}}\right)}=10.73 \times 10^{6} \mathrm{C}\]
where \(M_{Al}\) is the molecular weight.
Since E = QV, the electrical energy consumed for producing 1 kg of Al:
≈ Q × Ecell = (10.73 × 106)∙5 ≈ 50 MJ
The value calculated above assumes that there is 100% current efficiency. In fact, the current efficiency is usually 85-95%. The energy required increases as a result to ≈ 55 MJ kg-1. It should be noted that hydroelectric power is 90% efficient, and some aluminium plants have been preferentially located adjacent to these hydroelectric plants.
However, the electrical energy is normally produced by burning fossil fuels that are only 30-40% efficient. The real energy expended in this procedure therefore is given by:
\[\frac{55 \times 10^{6}}{0.35} \approx 160-170 \mathrm{MJkg}^{-1}\]
The energy consumed in the Hall-Héroult process is then added to the other energy-consuming parts of the Al-production process to find a value for the amount of energy used to produce 1 kg of aluminium from ore:-
- Energy required for the Hall-Héroult process ≈ 165 MJ kg-1
- Energy required in producing C anode: ≈ 25 MJ kg-1
- Energy required in producing the electrolyte: ≈ 5–10 MJ kg-1
- Energy expended in the Bayer Process to produce Al2O3 ≈ 60 MJ kg-1
Therefore, the total energy ≈ 260 MJ kg-1
Currently, every year, the world uses 20 million tonnes of aluminium. This means that more than 200 million tonnes of coal (or the energy equivalent of an energy-producing fuel e.g. gas or oil) is required in power plants each year [3]. That is a huge amount of energy. In fact, it is the same amount as 300–500 cities consume in a year!
The energy invested in primary Aluminium production is preserved in the metal. Used aluminium products can be melted down into new Aluminium repeatedly, although this process is not without complications, as are explained later in this learning package. To find out how much energy is saved by recycling aluminium, the total energy for primary aluminium production needs to be compared with the energy required to produce the same amount of aluminium by recycling.
Recycling Aluminium
Most of the energy required in the recycling of aluminium comes from the heating, and can be calculated by adding:
Energy to heat the aluminium from room temperature to the melting point + energy required for latent heat of melting + energy required to heat up molten aluminium to the casting temperature
\[\int_{298}^{933} C_{P}(A l(s)) d T + \Delta H_{933}^{0}(m) \int_{933}^{1000} C_{P}(A l(l)) d T\]
\[=\int_{298}^{933} C_{P}(A l(s)) d T+\Delta H_{933}^{0}(m)+\int_{933}^{1000} C_{P}(A l(l)) d T\]
where:
\[\begin{array}{l}
C_{P}(A l(s))=20.67+12.38 \times 10^{-3} \mathrm{TJmol}^{-1} \\
\Delta H_{933}^{0}(m)=10.7 \mathrm{kJmol}^{-1} \\
C_{P}(A l(l)) \approx 25.3 \mathrm{kJmol}^{-1}
\\ M_{Al} = 27 g mol^{-1}\end{array}\]
Thus, in
\[1 \mathrm{~kg}=\frac{1000}{27}=37.037 \mathrm{molkg}^{-1}\]
From these data the energy required (assuming an efficiency of 60-80%) can be calculated at approximately 6–10 MJ kg-1 (The proof is left to the reader![]() ).
).
Therefore even with the excess energy required to process the aluminium before it is re-melted, the energy expended is very significantly lower than creating new metal from ore:
260 MJ kg-1 >> 6–10 MJ kg-1
Some energy, it should be noted, is used in the sorting and processing of the metal scrap. ‘Processing’ including de-coating of the lacquer layers and shredding before it reaches the melting stage. Energy is also used in the transport of the scrap to the recycling plant, which may evoke concerns about the emissions from vehicular transport. Nevertheless, if these emissions are compared with the emissions from the power stations producing the electricity for the primary process they become negligible. An estimate of the energy used in vehicular transport can be found in the TLP on recycling of polymers, click here. It is possible to do a similar calculation for the transport of aluminium.
If recycling is an economically sound process – how does materials science contribute to the industrial methods used to recycle metals?


