6.2: Stiffness of Long Fiber Composites

Before we go into the details it is worth noting that the most suitable material for a given application may well not be the stiffest material. For example, for a given force applied to the free end of a cantilevered composite beam, the minimum deflection per unit mass is achieved by maximizing the merit index E / ρ².

Click here for Merit index derivation. (See Optimisation of Materials Properties in Living Systems for more on merit indices)

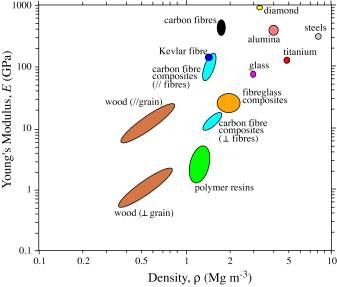
An Ashby property map (Young's Modulus against Density) for composites:

The axial and transverse Young's Moduli can be predicted using a simple slab model, in which the fibre and matrix are represented by parallel slabs of material, with thicknesses in proportion to their volume fractions, E and (1- E).

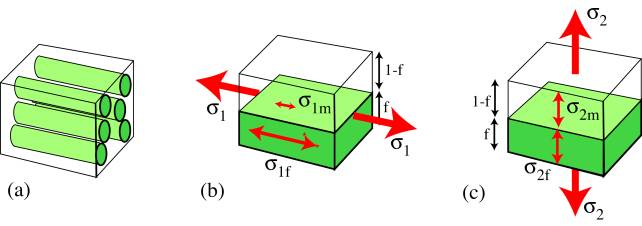
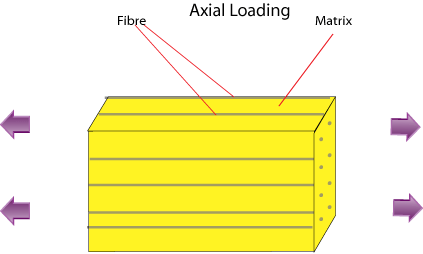
Axial Loading: Voigt model

The fibre strain is equal to the matrix strain: EQUAL STRAIN.

ε1=ε1f=σ1fEf=ε1m=σ1mEm=σ1E1

\[\varepsilon_{1}=\varepsilon_{1 f}=\frac{\sigma_{1 f}}{E_{f}}=\varepsilon_{1 m}=\frac{\sigma_{1 m}}{E_{m}}=\frac{\sigma_{1}}{E_{1}}\]

See definitions of terms

For a composite in which the fibres are much stiffer than the matrix ( E_f >> E_m ), the reinforcement fibre is subject to much higher stresses ( σ_1f >> σ_1m ) than the matrix and there is a redistribution of the load. The overall stress σ₁ can be expressed in terms of the two contributions:

\[\sigma_{1}=(1-f) \sigma_{1 \mathrm{m}}+f \sigma_{1 f}\]

The Young's modulus of the composite can now be written as

\[E_{1}=\frac{\sigma_{1}}{\varepsilon_{1}}=\frac{(1-f) \sigma_{1 \mathrm{m}}+f \sigma_{1 \mathrm{f}}}{\left(\frac{\sigma_{1 \mathrm{f}}}{E_{\mathrm{f}}}\right)}=(1-f) E_{\mathrm{m}}+f E_{\mathrm{f}}\]

This is known as the "Rule of Mixtures" and it shows that the axial stiffness is given by a weighted mean of the stiffnesses of the two components, depending only on the volume fraction of fibres.

Transverse Loading: Reuss Model

The stress acting on the reinforcement is equal to the stress acting on the matrix: EQUAL STRESS.

\[\sigma_{2}=\sigma_{2 f}=\varepsilon_{2 f} E_{f}=\sigma_{2 m}=\varepsilon_{2 m} E_{m}\]

The net strain is the sum of the contributions from the matrix and the fibre:

\[\varepsilon_{2}=f \varepsilon_{2 \mathrm{f}}+(1-f) \varepsilon_{2 \mathrm{m}}\]

from which the composite modulus is given by:

\[E_{2}=\frac{\sigma_{2}}{\varepsilon_{2}}=\frac{\sigma_{2 \mathrm{f}}}{f \varepsilon_{2 \mathrm{f}}+(1-f) \varepsilon_{2 \mathrm{m}}}=\left[\frac{f}{E_{\mathrm{f}}}+\frac{(1-f)}{E_{\mathrm{m}}}\right]^{-1}\]

This "Inverse Rule of Mixtures" is actually a poor approximate for E₂ since in reality regions of the matrix 'in series' with the fibres, close to them and in line along the loading direction, are subjected to a high stress similar to that carried by the reinforcement fibres; whereas the regions of the matrix 'in parallel' with the fibres (adjacent laterally) are constrained to have the same strain as the fibres and carry a low stress. This leads to non-uniform distributions of stress and strain during transverse loading, which means that the model is inappropriate. The slab model provides the lower bound for the transverse stiffness.

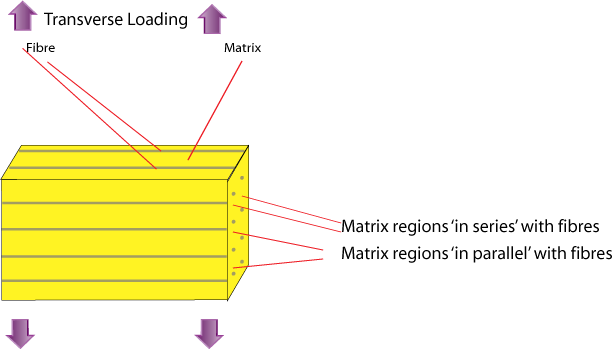
A more successful estimate is the semi-empirical Halpin-Tsai expression:

\[E_{2}=\frac{E_{m}(1+\xi \eta f)}{(1-\eta f)}\]

where

\[\eta=\frac{\left(\frac{E_{f}}{E_{m}}-1\right)}{\left(\frac{E_{f}}{E_{m}}+\xi\right)} \text { and } \xi \approx 1\]

An even more powerful, but complex, analytical tool is the Eshelby method (see Hull and Clyne, 1996).

---