6.12: Questions
- Page ID
- 35958
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Quick questions
You should be able to answer these questions without too much difficulty after studying this TLP. If not, then you should go through it again!
In mechanical loading experiments, involving large stresses and long durations, to measure the transverse stiffness of a composite, the experimental values are sometimes lower than the Halpin-Tsai prediction (some even lower than the Equal stress calculation.) Why might this be?
- Answer
-
Correct. Inelastic deformation and creep of the matrix increases the strain for a given applied stress. Since
\[E=\frac{\sigma}{\varepsilon}\]
a larger strain leads to a smaller Young’s Modulus.
How would you determine the total energy absorbed during fracture of a composite from its stress strain curve? (multiple choice)
- Answer
-
B
\[\begin{array}{l}
\sigma=\frac{\text {Force}}{\text {Area}}, \quad \varepsilon=\frac{\text {Extension in the direction of the force}}{\text {Original length}} \quad \sigma \times \varepsilon=\frac{\text {Force} \times \text {Extension}}{\text {Volume}} \\
\text {Work done}=\text {Force} \times \text {Extension}=\sigma \times \varepsilon \times \text {volume}
\end{array}\]
What is the most significant energy absorbing mechanism during composite failure?
- Answer
-
D. Additional work is required for frictional sliding
What is the combined work done per unit crack area required for crack deflection and fibre pull-out in a 60 % long-fibre composite? (Data: τi* = 40 MPa, Gic = 8 J m-2 , fibre radius r = 7 μm, pull-out length x0 = 840 μm.)
- Answer
-
C
Pull-out aspect ratio s = xo / 2r = 840 / (2*7) = 60
\[\begin{array}{l}
G_{c d}=f_{S} G_{i c}=0.6 \times 60 \times 8=288 \mathrm{Jm}^{-2} \\
G_{\mathrm{cp}}=4 \mathrm{fs}^{2} r \tau_{\mathrm{i}^{*}}=4 \times 0.6 \times 60^{2} \times\left(7 \times 10^{-6}\right) \times\left(40 \times 10^{6}\right)=2.4 \mathrm{MJ} \mathrm{m}^{-2}
\end{array}\]
∴ Work per unit crack area ≈ 2.4 MJ m-2.
Deeper questions
The following questions require some thought and reaching the answer may require you to think beyond the contents of this TLP.
For a laminate made up of 50% volume fraction carbon HS fibres and Nylon 6,6 matrix with a stacking sequence of 0 / 15 /50 / 55 / 60, at what loading angle is the Poisson contraction the minimum?
- Answer
-
D
How would you describe a laminate, composed of two constituents, with a stacking sequence of 0/45/80/45/0 subjected to a uniaxial tensile stress at a loading angle of 20 degrees?
- Answer
-
C
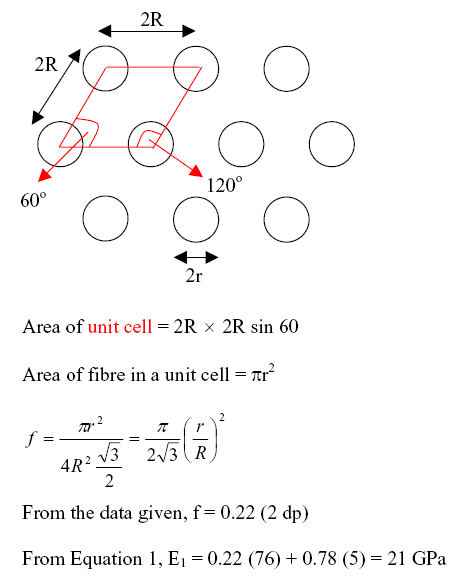
What is the axial stiffness of a long-fibre composite composed of glass fibres arranged in a hexagonal array in an epoxy matrix ? (Data: Glass fibre: Ef = 76 , fibre radius = 3.9 μm, spacing between centres of adjacent fibres = 8 μm Epoxy: Em = 5 GPa.)
- Answer
-
Correct.
Calculate the axial failure stress for a composite composed of 30% borosilicate glass matrix and 70 % kevlar fibre, assuming that if one of the components fails the entire applied load is transferred to the other component.
Data: Kevlar fibre: σfu = 3.0 GPa, Ef = 130 GPa.
Borosilicate glass matrix: σmu = 0.10GPa, Em = 64 GPa
What further assumptions do you need to make?
- Answer
-
Correct.
