1.7: Advanced Topic- Derivation of the Strain-Displacement Relation for Thin Plates
- Page ID
- 21692
The Love-Kirchoff hypothesis extends the one-dimensional Euler-Bernoulli assumptions into plates. A plate can be bent in two directions, forming a double curvature surface. Therefore the plane-remains-plane and normal-remains-normal properties are now required in both directions. Thus, Equation (1.5.1) and Equation (1.5.2) take the form
\[u_{\alpha} = u_{\alpha}^{\circ} - \theta_{\alpha} z\]
\[\theta_{\alpha} = \frac{\partial w}{\partial x_{\alpha}} \buildrel \rm {def} \over{=} w_{,\alpha}\]
where \(\theta_{\alpha}\) is the slope (rotation) in \(x_{\alpha}\)-direction. Upon elimination of \(\theta_{\alpha}\) between the above equation, one gets the familiar linear dependence of the in-plane components of the displacement vector on the z-coordinate
\[u_{\alpha}(x_{\alpha}, z) = u_{\alpha}^{\circ}(x_{\alpha}) − zw_{,\alpha} \label{1.7.3}\]
The constant thickness \((w = \dot{w}(x_{\alpha}))\) is the third kinematic assumption of the plate theory.
Now, watch carefully how the strain components in the plate are calculated. Considering all components of the strain tensor, one can distinguish three in-plane strain components \(\epsilon_{\alpha \beta}\) (framed area on the matrix below) and three out-of-plane components.
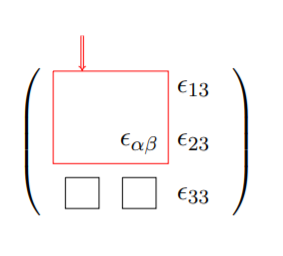
The through thickness strain component vanishes on the assumption of independence of the vertical displacement on the coordinate \(z\)
\[\epsilon_{33} = \epsilon_{zz} = \frac{\delta w}{\delta z} = 0\]
The two out-of-plane shear components of the strain tensor \(\epsilon_{\alpha 3}\) vanish due to the LoveKirchoff hypothesis, Equation \ref{1.7.3},
\[\epsilon_{\alpha 3} = \frac{1}{2} \left( \frac{\delta u_{\alpha}}{\delta z} + \frac{\delta w}{\delta x_{\alpha}} \right) = \frac{1}{2} (u_{\alpha , z} + w_{, \alpha}) = \frac{1}{2} \left[ \frac{d}{d z} (u_{\alpha}^{\circ}(x_{\alpha}) + w_{,\alpha} \right] = 0\]
The non-vanishing components of the strain tensor are the in-plane strain components
\[\epsilon_{\alpha \beta} = \frac{1}{2} (u_{\alpha , \beta} + u_{\beta , \alpha}) \alpha, \beta = 1, 2\]
where \(u_{\alpha}\) is defined by Equation (1.3.9). Performing the differentiation one gets
\[\epsilon_{\alpha \beta} = \frac{1}{2} [ u_{\alpha}^{\circ} - zw_{, \alpha}]_{, \beta} + \frac{1}{2} [ u_{\beta}^{\circ} − zw_{,\beta}]_{, \alpha} = \frac{1}{2} (u_{\alpha , \beta}^{\circ} + u_{\beta , \alpha}^{\circ}) - \frac{1}{2} z [ w_{,\alpha \beta} + w_{,\beta \alpha}] \label{1.7.7}\]
The first term in Equation \ref{1.7.7} is the strain \(\epsilon_{\alpha \beta}^{\circ}\) arising from the membrane action in the plate. It is a symmetric gradient of the middle plane displacement \(u_{\alpha}^{\circ}\). Since the order of partial differentiation is not important, Equation \ref{1.7.7} simplifies to
\[\epsilon_{\alpha \beta}(x_{\alpha}, z) = \epsilon_{\alpha \beta}^{\circ}(x_{\alpha}) − zw_{,\alpha \beta}\]
Defining the curvature tensor \(\kappa_{\alpha \beta}\) by
\[\kappa_{\alpha \beta} = −w_{,\alpha \beta} = − \frac{\partial^2 w}{\partial x_{\alpha} \partial x_{\beta}}\]
The strain-displacement relation for thin plates takes the final form
\[\epsilon_{\alpha \beta} = \epsilon_{\alpha \beta}^{\circ} + z\kappa_{\alpha \beta}\]
where
\[\epsilon_{\alpha \beta}^{\circ} = \frac{1}{2}(u_{\alpha , \beta}^{\circ} + u_{\beta , \alpha}^{\circ})\]


