1.8: Expanded Form of Strain-Displacement Relation
- Page ID
- 21694
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Having derived the geometric relations in the tensorial notations, equations (1.7.10) and (1.7.11) will be re-written in the coordinate system (x, y) and physical interpretation will be given to each term. Consider first (1.7.11)
\[\alpha = 1, \beta = 1 \; x_1 = x, \; \epsilon_{xx}^{\circ} = \frac{1}{2} \left( \frac{\partial u_{x}^{\circ}}{\partial x} + \frac{\partial u_{x}^{\circ}}{\partial x} \right) = \frac{\partial u_{x}^{\circ}}{\partial x} \]
\[\alpha = 2, \beta = 2 \; x_2 = y, \; \epsilon_{xx}^{\circ} = \frac{1}{2} \left( \frac{\partial u_{y}^{\circ}}{\partial y} + \frac{\partial u_{y}^{\circ}}{\partial y} \right) = \frac{\partial u_{y}^{\circ}}{\partial y} \]
\[\alpha = 1, \beta = 2 \; x_1 = x, x_2 = y, \; \epsilon_{xy}^{\circ} = \frac{1}{2} \left( \frac{\partial u_{x}^{\circ}}{\partial y} + \frac{\partial u_{y}^{\circ}}{\partial x} \right) \]
The \(\epsilon_{xx}^{\circ}\) and \(\epsilon_{yy}^{\circ}\) components denote strains of the middle surface of the plate in the \(x\) and \(y\) directions, respectfully. The membrane strains are due to the imposed displacements or membrane forces applied to the edges. In the theory of small deflection of plates, lateral pressure loading will not produce membrane strains. By contrast, membrane strains do develop in the theory of moderately large deflection of plates due to transverse loading. This topic will be covered later in Chapter 6.
The third component of the strain tensor is the in-plane shear strain \(\epsilon_{xy}^{\circ}\). It represents the change of angles in the plane of the plate due to the shear loading at the edges. The geometrical interpretation of the membrane strain tensor is similar to that given for the general strain tensor in Figures (1.2.2) and (1.2.3).
The curvature tensor \(\kappa_{\alpha \beta}\) requires a careful explanation. Consider an infinitesimal segment ds of a curve and fit into it a circle of an instantaneous radius ρ, Figure (\(\PageIndex{1}\)). Then
\[ds = \rho d\theta \]
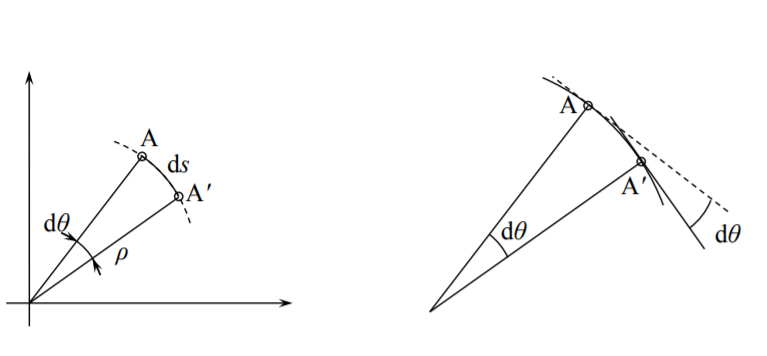
Mathematically, the curvature of any line \(\kappa\) is the change of the slope as one moves along the curve
\[\kappa \buildrel \rm {def} \over{=} \frac{d\theta }{ds} \label{1.8.5}\]
By comparing Equation \ref{1.8.5} with Equation (1.7.2), the curvature in \([ \frac{1}{m} ]\) is the reciprocity of the radius of curvature \(\kappa = \frac{1}{\rho}\). The first component of the curvature tensor, defined by Equation (1.7.10) is
\[\alpha = 1, \beta = 1 \; x_1 = x \; \kappa_{xx} = -\frac{\partial^2 w}{\partial x^2} = -\frac{\partial}{\partial x} \left( \frac{\partial w}{\partial x} \right) = \frac{\partial}{\partial x} ( - \theta_{x})\]
This will be the only component of the curvature tensor if the plate is subject to the so-called cylindrical bending.
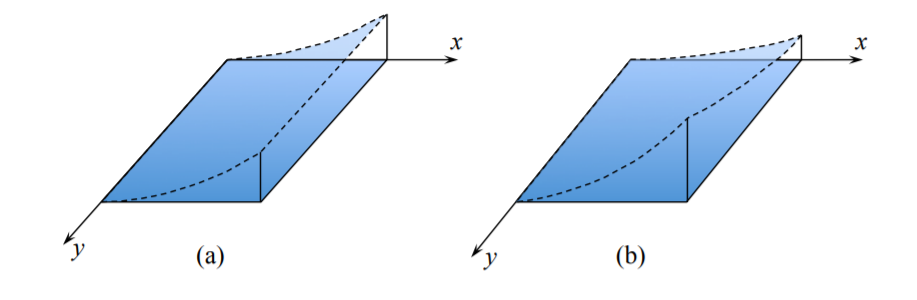
The interpretation of the \(\kappa_{yy}\) components of the curvature tensor
\[\alpha = 2, \beta = 2 \; x_2 = y \; \kappa_{yy} = -\frac{\partial^2 w}{\partial y^2} = -\frac{\partial}{\partial y} ( - \theta_{y})\]
is similar as before. More interesting is the mixed component of the curvature tensor
\[\alpha = 1, \beta = 2 \; x_1 = x, x_2 = y \; \kappa_{xy} = -\frac{\partial^2 w}{\partial x \partial y} = -\frac{\partial}{\partial y} ( - \theta_{x})\]
To detect \(\kappa_{xy}\) one has to check if the slope in one direction, say \(\theta_x\) changes along the second \(y\)-direction. It does not for a cylindrical bending, Figure (1.4.2(a)). But if it does, the plate is twisted, as shown in Figure (1.4.2(b)). Therefore, the component \(\kappa_{xy}\) is called a twist.
An important parameter that distinguishes between these classes of the deformed shape of a plate is the Gaussian curvature, \(\kappa_{G}\). The Gaussian curvature is defined as a product of two principal curvatures
\[\kappa_{G} = \kappa_I\kappa_{II}\]
The curvature is a tensor, so its components change by rotating the coordinate system by an angle \(\psi\) to a new direction (x\prime , y\prime ). There is one such an angle \(\psi_p\) for which the twisting components vanish. The remaining diagonal components are called principal curvature. The full coverage of the transformation formulae for vectors and tensors are presented in Recitation 2. Using these results, the Gaussian curvature can be expressed in terms of the components of the curvature tensor
\[\kappa_{G} = \kappa_{xx} \kappa_{yy} − \kappa_{xy}^2\]
For cylindrical bending the twist κxy as well as one of the principal curvatures vanishes so that the Gaussian curvature is zero. The sign of the Gaussian curvature distinguishes between three types of the deformed plate, the bowl, the cylinder and the saddle, Figure (\(\PageIndex{3}\)).

The consideration of Gaussian curvature introduces important simplifications in formulation and applications of the energy method in structural mechanics. A separate lecture will be devoted to this topic.


