10.5: Polar Moment of Inertia

Last updated
Save as PDF

Page ID: 70287

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Key Questions

How are polar moments of inertia similar and different to area moments of inertia about either a horizontal or vertical axis?

The polar moment of inertia is defined by the integral quantity

\begin{equation} J_O = \int_A r^2 dA\text{,}\tag{10.5.1} \end{equation}

where \(r\) is the distance from the reference point to a differential element of area \(dA\text{.}\)

The polar moment of inertia describes the distribution of the area of a body with respect to a point in the plane of the body. Alternately, the point can be considered to be where a perpendicular axis crosses the plane of the body. The subscript on the symbol \(j\) indicates the point or axis.

There is a particularly simple relationship between the polar moment of inertia and the rectangular moments of inertia. Referring to the figure, apply the Pythagorean theorem \(r^2 = x^2 +y^2\) to the definition of polar moment of inertia to get

\begin{align*} J_O & = \int_A r^2\ dA\notag \\ & = \int_A (x^2 + y^2) \ dA\notag\\ &= \int_A x^2 dA + \int_A y^2 dA\notag\\ J_O & = I_x + I_y\text{.}\label{Jo}\tag{10.5.2} \end{align*}

Thinking Deeper 10.5.1. Torsional Stress.

The polar moment of inertia is an important factor in the design of drive shafts. When a shaft is subjected to torsion, it experiences internal distributed shearing forces throughout its cross-section which counteract the external torsional load.

This distributed shearing force is called shear stress, and is usually given the symbol tau, \(\tau\text{.}\) Shear stress is zero at the neutral axis and increases linearly with \(r\) to a maximum value, \(\tau_\text{max}\) at the outside surface where \(r=c\text{,}\) so

\[ \tau = \tau_\text{max}\frac{r}{c} \nonumber \]

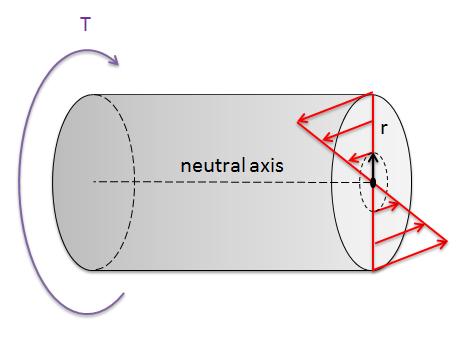
undefined

Figure 10.5.2. Section-cut view of a shaft, showing shearing forces developed to withstand external torsion \(T\text{.}\)

The force at any point is \(dF = \tau\ dA\text{,}\) and the moment \(dM\) exerted at any point is \(dF\) times the moment arm, which is \(r\text{.}\) The total moment is the integral of this quantity over the area of the cross section, and is proportional to the polar moment of inertia.

\begin{align*} T &= \int dM\\ & = \int r\ dF\\ &= \int_A r\ \tau_\text{max} \frac{r}{c} \ dA\\ &= \frac{\tau_\text{max}}{c} \int_A r^2\ dA\\ T & = \frac{\tau_\text{max}}{c} J\\ \tau_\text{max} & = \frac{Tc}{J} \end{align*}

This is the relationship between the maximum stress in a circular shaft and the applied torque \(T\) and the geometric properties of the shaft, \(J_O\) and \(c\text{.}\)