12.3: Definitions

Unbalanced moments: This method of analysis assumes that the joints in a structure are initially clamped or locked and then released successively. Once a joint is released, a rotation takes place, since the sum of the fixed end moments of the members meeting at that joint is not zero. The value of the sum of the end moments obtained is the unbalanced moment at that joint.

Carry-over moments: The distributed moments in the ends of members meeting at a joint cause moments in the other ends, which are assumed to be fixed. These induced moments at the other ends are called carry-over moments.

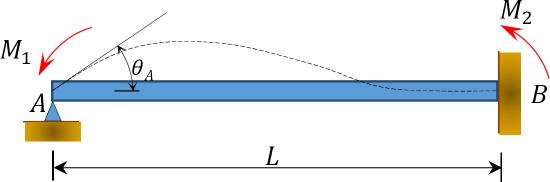
\(Fig. 12.2\). Unloaded prismatic beam.

Consider an unloaded prismatic beam fixed at end \(B\), as shown in Figure 12.2. If a moment \(M_{1}\) is applied to the left end of the beam, the slope-deflection equations for both ends of the beam can be written as follows:

\[M_{1}=2 E K\left(2 \theta_{A}\right)=4 E K \theta_{A} \label{1}\]

\[M_{2}=2 E K \theta_{A} \label{2}\]

Substituting \(\theta_{A}=\frac{M_{1}}{4 E K}\) from equation 12.1 into equation 12.2 suggest the following: \[M_{2}=\frac{1}{2} M_{1} \label{3}\]

Equation \ref{3} suggests that the moment carried over to the fixed end of a beam due to a moment applied at the other end is equal to one-half of the applied moment.

Carry-over factor: The ratio of the induced moment to the applied moment is referred to as the carry-over factor. For the beam shown in Figure 12.2, the carry-over factor is as follows: \[\frac{M_{2}}{M_{1}}=\frac{2 E K \theta_{A}}{4 E K \theta_{A}}=\frac{1}{2}\]

Distributed factor (DF): The distributed factor is a factor used to determine the proportion of the unbalanced moment carried by each of the members meeting at a joint. For the members meeting at joint \(O\) of the frame shown in Figure 12.3, their distribution factors are computed as follows:

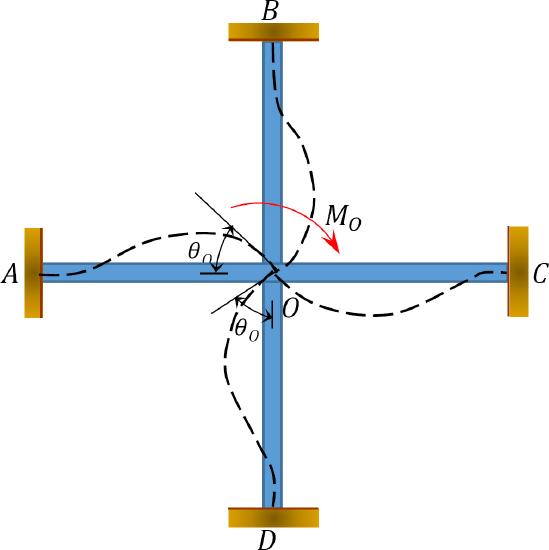
\(Fig. 12.3\). Frame.

\[\begin{array}{l}
(D F)_{O A}=\frac{K_{O A}}{\sum K} \\
(D F)_{O B}=\frac{K_{O B}}{\Sigma K} \\
(D F)_{O C}=\frac{K_{O C}}{\sum K} \\
(D F)_{O D}=\frac{K_{O D}}{\sum K}
\end{array}\]

Distributed moments: Upon the release of the imaginary clamp at a joint, the unbalanced moment at that joint causes it to rotate. The rotation twists the end of the members meeting at the joint, resulting in the development of resisting moments. These resisting moments are called distributed moments. The distributed moments for the members of the frame shown in Figure 12.3 are computed as follows: \[\begin{array}{l}
M_{O A}=\frac{K_{O A}}{\Sigma K} M_{O}=(D F)_{O A} M_{O} \\
M_{O B}=\frac{K_{O B}}{\sum K} M_{O}=(D F)_{O B} M_{O} \\
M_{O C}=\frac{K_{O C}}{\Sigma K} M_{O}=(D F)_{O C} M_{O} \\
M_{O D}=\frac{K_{O D}}{\Sigma K} M_{O}=(D F)_{O D} M_{O}
\end{array}\]