6.6: Entropy and entropy generation
- Page ID
- 88856
6.5.1 The inequality of Clausius
The inequality of Clausius states that for any cycle, reversible or irreversible, there exists the following relation:
\[\displaystyle\oint\dfrac{\delta Q}{T}\le0\ \ \ \ \ \ \ \ \mathrm{(``="\ for\ reversible\ cycles;\ ``<"\ for\ irreversible\ cycles)}\]
where 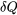 represents the differential amount of heat transfer into or out of a system through an infinitesimal part of the system boundary.
represents the differential amount of heat transfer into or out of a system through an infinitesimal part of the system boundary. 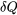 is positive for heat transfer into the system and is negative for heat transfer out of the system.
is positive for heat transfer into the system and is negative for heat transfer out of the system. 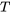 is the absolute temperature at the infinitesimal part of the system boundary, where the heat transfer occurs. The cyclic integral symbol
is the absolute temperature at the infinitesimal part of the system boundary, where the heat transfer occurs. The cyclic integral symbol 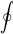 indicates that the integration must be done for the entire cycle. In other words, all heat transfer into and out of the system, as well as their corresponding boundary temperatures, must be considered in the integral.
indicates that the integration must be done for the entire cycle. In other words, all heat transfer into and out of the system, as well as their corresponding boundary temperatures, must be considered in the integral.
The inequality of Clausius applies to all cycles. We will prove it by using the heat engine cycle, Figure 6.1.3, as an example. For a reversible heat engine cycle operating between a heat source at a constant temperature of 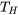 and a heat sink at a constant temperature of
and a heat sink at a constant temperature of 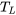 , the cyclic integral can be written as
, the cyclic integral can be written as
\[\displaystyle\oint\left(\dfrac{\delta Q}{T}\right)_{rev} = \left(\dfrac{Q_H}{T_H}\right)_{rev} + \left(\dfrac{-Q_L}{T_L}\right)_{rev}\]
Note that for a reversible cycle,
\[\left(\displaystyle\dfrac{T_H}{T_L}\right)_{rev} = \left(\displaystyle\dfrac{Q_H}{Q_L}\right)_{rev}\]
Therefore, the following equation exists for a reversible cycle.
\[\displaystyle\oint\left(\dfrac{\delta Q}{T}\right)_{rev} =0\]
For an irreversible cycle operating between the same two heat reservoirs at constant temperatures of 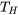 and
and 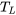 , we assume that the heat absorbed from the heat source,
, we assume that the heat absorbed from the heat source, 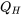 , remains the same as that in the reversible cycle,
, remains the same as that in the reversible cycle,
\[\because Q_{H, rev} = Q_{H, irrev} = Q_{H}\]
\[\therefore Q_{L, rev} < Q_{L, irrev}\]
\[\therefore \left(\dfrac{Q_H}{Q_L}\right)_{irrev} < \left(\dfrac{Q_H}{Q_L}\right)_{rev}\]
\[\therefore \left(\dfrac{Q_H}{Q_L}\right)_{irrev} < \left(\dfrac{T_H}{T_L}\right)_{rev}\]
\[\therefore \left(\dfrac{Q_H}{T_H}\right)_{irrev} < \left(\dfrac{Q_L}{T_L}\right)_{irrev}\]
Therefore,
\[\displaystyle\oint\left(\dfrac{\delta Q}{T}\right)_{irrev} = \left(\dfrac{Q_H}{T_H}+\dfrac{-Q_L}{T_L}\right)_{irrev} = \left(\dfrac{Q_H}{T_H}\right)_{irrev} - \left(\dfrac{Q_L}{T_L}\right)_{irrev} < 0\]
Now, we have proven the inequality of Clausius for heat engine cycles. A similar procedure may be applied to prove the inequality of Clausius for refrigerator and heat pump cycles.
6.5.2 Definition of entropy
Why is the inequality of Clausius important? The cyclic integral is either equal to or less than zero depending on the nature of the cycle: reversible or irreversible. The inequality of Clausius provides a basis for introducing the concepts of entropy and entropy generation. Both concepts are important in the second law of thermodynamics.

Let us apply the inequality of Clausius to a reversible cycle consisting of two reversible processes 1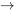 2 via path A and 2
2 via path A and 2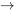 1 via path B, see Figure 6.5.1.
1 via path B, see Figure 6.5.1.
\[\begin{align*} \because \displaystyle\oint \left(\dfrac{\delta Q}{T}\right)_{rev} &= \int_{1}^{2}\left(\dfrac{\delta Q}{T}\right)_{path A} + \int_{2}^{1}\left(\dfrac{\delta Q}{T}\right)_{path B} \\ &= \int_{1}^{2}\left(\dfrac{\delta Q}{T}\right)_{path A} - \int_{1}^{2}\left(\dfrac{\delta Q}{T}\right)_{path B}=0 \end{align*}\]
\[\therefore \displaystyle\int_{1}^{2}\left(\displaystyle\frac{\delta Q}{T}\right)_{path A} = \displaystyle\int_{1}^{2}\left(\displaystyle\frac{\delta Q}{T}\right)_{path B}\]
\[S\]
\[\displaystyle\Delta S = S_2-S_1=\int_{1}^{2}\left(\displaystyle\frac{\delta Q}{T}\right)_{rev}\]
The infinitesimal change of entropy in a reversible process can thus be written as
\[dS=\left(\dfrac{\delta Q}{T}\right)_{rev}\]
where 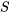 is the entropy and
is the entropy and 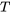 is the absolute temperature. The common SI units for entropy are kJ/K or J/K. It is important to note that entropy,
is the absolute temperature. The common SI units for entropy are kJ/K or J/K. It is important to note that entropy, 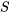 , is a state function;
, is a state function;  in a process depends on the initial and final states, not on the path of the process.
in a process depends on the initial and final states, not on the path of the process.
Entropy is an extensive property; its corresponding intensive property is called specific entropy, 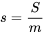 , and its common SI units are kJ/kgK or J/kgK.
, and its common SI units are kJ/kgK or J/kgK.
Example 1
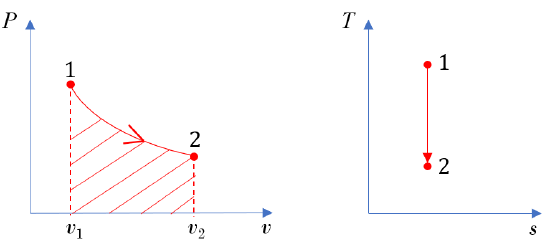
Consider a reversible process and an irreversible process from states 1 to 2, as shown in the T-S diagram, Figure 6.5.e1. Answer the following questions
(1) Is the change in entropy, ΔS, the same or different in these two processes?
(2) Is it possible to show the heat transfer of the reversible process in the T-S diagram?
(3) Is it possible to show the heat transfer of the irreversible process in the T-S diagram?

Solution:
(1) Entropy is a state function. The two processes have the same initial and final states, therefore, the same ΔS.
(2) From the definition of entropy, the heat transfer in the reversible process can be found from
\[Q_{rev}=\displaystyle\int_{1}^{2} {\left(\delta Q\right)}_{rev} = \int_{1}^{2} \left(TdS\right)_{rev}\]
This integral can be shown graphically as the shaded area under the T-S curve of the reversible process, see Figure 6.5.e2.

(3) The heat transfer of the irreversible process cannot be simply calculated without additional information, and it cannot be shown in the T-S diagram.
Example 2
A reversible process from states 1 2 in a piston-cylinder is shown in Figure 6.5.e3. Determine whether the change in specific internal energy
2 in a piston-cylinder is shown in Figure 6.5.e3. Determine whether the change in specific internal energy 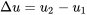 , specific work w, and specific heat transfer q are positive, zero, or negative.
, specific work w, and specific heat transfer q are positive, zero, or negative.
Solution:
The 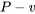 diagram shows an expansion process in the piston-cylinder. Its specific boundary work can be shown as the shaded area in the
diagram shows an expansion process in the piston-cylinder. Its specific boundary work can be shown as the shaded area in the 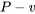 diagram, see Figure 6.5.e3. It can also be expressed as
diagram, see Figure 6.5.e3. It can also be expressed as
\[{}_{1}w_{2} = \displaystyle\int_{1}^{2} Pdv > 0\]
From the definition of entropy,
\[dS=\left(\displaystyle\frac{\delta Q}{T}\right)_{rev}\]
The process is reversible; therefore,
\[(\delta Q)_{rev} = TdS\]
\[\therefore \; {}_{1}Q_{2} = Q_{rev} = \displaystyle\int_{1}^{2} (\delta Q)_{rev} = \displaystyle\int_{1}^{2} TdS \]
The specific heat transfer is
\[{}_{1}q_{2} = \dfrac
Callstack:
at (Bookshelves/Mechanical_Engineering/Introduction_to_Engineering_Thermodynamics_(Yan)/06:_Entropy_and_the_Second_Law_of_Thermodynamics/6.06:_Entropy_and_entropy_generation), /content/body/div[2]/p[31]/span, line 1, column 1
From the 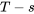 diagram in Figure 6.5.e3,
diagram in Figure 6.5.e3, 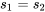 ; therefore,
; therefore,
\[{}_{1}q_{2} = 0\]
The specific heat transfer in a reversible process can be shown graphically as the area under the process line in the 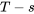 diagram. Note: this statement is only true for reversible processes; it is not valid for irreversible processes!
diagram. Note: this statement is only true for reversible processes; it is not valid for irreversible processes!
Apply the first law of thermodynamics to the piston-cylinder (closed system),
\[\Delta u = {}_{1}q_{2} - {}_{1}w_{2} = 0 - {}_{1}w_{2} < 0\]
In conclusion, the reversible expansion process illustrated in the 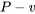 and
and 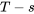 diagrams in Figure 6.5.e3 has a positive boundary work and zero heat transfer (adiabatic). The specific internal energy decreases in the process.
diagrams in Figure 6.5.e3 has a positive boundary work and zero heat transfer (adiabatic). The specific internal energy decreases in the process.
6.5.3 Entropy generation, Sgen
Entropy generation is another important concept in the second law of thermodynamics. Let us consider a cycle consisting of two processes; process 2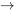 1 is a reversible process and process 1
1 is a reversible process and process 1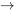 2 can be any process, either reversible or irreversible, see Figure 6.5.2. We will apply the definition of entropy and the inequality of Clausius in the following derivations.
2 can be any process, either reversible or irreversible, see Figure 6.5.2. We will apply the definition of entropy and the inequality of Clausius in the following derivations.
\[\because \Delta S = S_2-S_1=\displaystyle\int_{1}^{2}\left(\dfrac{\delta Q}{T}\right)_{rev}\]
\[\begin{align*} \therefore\displaystyle\oint \dfrac{\delta Q}{T} &= \displaystyle\int_{1}^{2}\left(\displaystyle\frac{\delta Q}{T}\right) + \displaystyle\int_{2}^{1}\left(\displaystyle\frac{\delta Q}{T}\right)_{rev} \\&= \displaystyle\int_{1}^{2}\left(\displaystyle\frac{\delta Q}{T}\right) - \displaystyle\int_{1}^{2}\left(\displaystyle\frac{\delta Q}{T}\right)_{rev} \\ &= \displaystyle\int_{1}^{2}\left(\displaystyle\frac{\delta Q}{T}\right) - (S_2 - S_1) \le 0 \end{align*}\]
\[\therefore (S_2-S_1) \ge \displaystyle\int_{1}^{2}\left(\displaystyle\frac{\delta Q}{T}\right)\]
We may change the above inequality to an equation by introducing entropy generation, 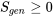 , to the right side; therefore,
, to the right side; therefore,
\[\Delta S = (S_2-S_1) = \displaystyle\int_{1}^{2}\left(\displaystyle\frac{\delta Q}{T}\right) + S_{gen} \hspace{3em} \left( S_{gen} \ge 0\right)\]
This relation is valid for all processes with the “ ” sign for reversible processes, and the “
” sign for reversible processes, and the “" class="latex mathjax" title=">" src="/@api/deki/files/59059/95a81a28652c14c0562699985a262099.png">” sign for irreversible processes. The differential form of the relation can be expressed as
\[dS=\displaystyle\frac{\delta Q}{T}+\delta S_{gen} \hspace{3em} \left( \delta S_{gen} \ge 0\right)\]
It is important to note that 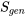 and
and  are different concepts.
are different concepts.
- Entropy generation,
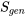 , is a measure of the irreversibilities in a process.
, is a measure of the irreversibilities in a process. 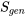 is NOT a property of the system. It depends on the path of a process; the more irreversible a process is, the larger
is NOT a property of the system. It depends on the path of a process; the more irreversible a process is, the larger 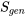 is.
is. - Entropy
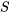 is a thermodynamic property of the system. It is a state function.
is a thermodynamic property of the system. It is a state function.  depends on the initial and final states only, not on the path of a process.
depends on the initial and final states only, not on the path of a process. - In general,
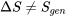 .
.  may be positive or negative, but
may be positive or negative, but 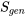 must be positive for irreversible processes or zero for reversible processes.
must be positive for irreversible processes or zero for reversible processes.
Why is entropy generation important? how does it play a role in the universe? The universe is everything, including all the matter and energy that could possibly exist in all space and time. We may treat the universe as an isolated system because nothing exists outside the universe. From the entropy generation, 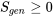 , we can prove that the entropy in the universe always increases due to the existence of irreversibilities in nature and in all human activities.
, we can prove that the entropy in the universe always increases due to the existence of irreversibilities in nature and in all human activities.

Let us define a system in the universe and everything outside the system boundary as the surroundings, see Figure 6.5.3. The change of entropy in the universe can be written as
\[\Delta S_{univ} = \Delta S_{sys} + \Delta S_{sur}\]
where 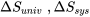 , and
, and 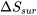 represent the changes of entropy in the universe, the system, and its surroundings, respectively.
represent the changes of entropy in the universe, the system, and its surroundings, respectively.
The change of entropy in the universe can be written in terms of entropy generation as
\[\Delta S_{univ} = \displaystyle\int_{1}^{2}\left(\dfrac{\delta Q}{T}\right) + (S_{gen})_{univ}\]
Since the universe is an isolated system, heat transfer across the universe boundary 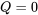 . In addition, since all real processes happening in the universe are irreversible, we can drop the “
. In addition, since all real processes happening in the universe are irreversible, we can drop the “ ” sign in the inequality; therefore,
” sign in the inequality; therefore,
\[(S_{gen})_{univ} = \Delta S_{univ} = \Delta S_{sys} + \Delta S_{sur} > 0\]
The above relation indicates that the entropy generation in the universe is always a positive number due to the irreversibilities in all real processes. As a result, the entropy in the universe always increases. This concept can be expressed in a general format as follows if we divide the universe into a number of subsystems.
\[(S_{gen})_{univ} = \Delta S_{univ} = \Delta S_{sys,1} + \Delta S_{sys,2} +...+\Delta S_{sys,n}= \sum_{i=1}^{n}\Delta S_{sys,i} > 0\]
where 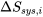 is the change of entropy in the subsystem, i, in the universe.
is the change of entropy in the subsystem, i, in the universe.
6.5.4 The second law of thermodynamics expressed in terms of entropy generation, Sgen
The second law of thermodynamics was previously described with the Kelvin-Planck and Clausius statements. In fact, any device that violates the Kelvin-Planck or Clausius statements must have 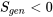 .
.
Take a heat pump as an example. We may prove that any heat pump that violates the Clausius statement would have 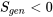 . A heat pump that violates the Clausius statement would have
. A heat pump that violates the Clausius statement would have 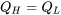 from the first law of thermodynamics, see Figure 6.5.4. Note that entropy is a state function. For the heat pump cycle, the initial and final states are the same; therefore,
from the first law of thermodynamics, see Figure 6.5.4. Note that entropy is a state function. For the heat pump cycle, the initial and final states are the same; therefore, 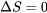 . The change of entropy in the heat pump cycle can be expressed as follows,
. The change of entropy in the heat pump cycle can be expressed as follows,
\[\because \Delta S = \displaystyle \int_{1}^{2}\left(\displaystyle\frac{\delta Q}{T}\right) + S_{gen} = \dfrac{-Q_H}{T_H} + \dfrac{Q_L}{T_L} + S_{gen} =0\]
\[\therefore S_{gen} = \dfrac{Q_H}{T_H} - \dfrac{Q_L}{T_L} = Q_H\left(\dfrac{1}{T_H} - \dfrac{1}{T_L}\right) < 0\]

Now, we have proven that any heat pump that violates the Clausius statement would have 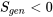 . A similar procedure may be applied to prove that any heat engine that violates the Kelvin-Planck statement would have
. A similar procedure may be applied to prove that any heat engine that violates the Kelvin-Planck statement would have 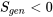 .
.
In summary, the second law of thermodynamics requires that any process or cycle proceeds in the direction that obeys 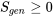 , in which the “
, in which the “ ” sign applies to the ideal Carnot cycles and the “
” sign applies to the ideal Carnot cycles and the “" class="latex mathjax" title=">" src="/@api/deki/files/59059/95a81a28652c14c0562699985a262099.png">” sign applies to any real, irreversible cycles or processes.
- Actual, irreversible process or cycle:
0" class="latex mathjax" title="S_{gen}>0" src="/@api/deki/files/59082/06b0297b8c94b487262b45bd7b0793b8.png">
- Carnot, reversible process or cycle:
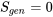
- Impossible process or cycle:
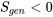
Query \(\PageIndex{1}\)


