6.8: Specific entropy of a state

Last updated
Save as PDF

Page ID: 88858

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

6.7.1 Determining the specific entropy of pure substances by using thermodynamic tables

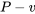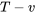The specific entropy of a pure substance can be found from thermodynamic tables if the tables are available. The procedures are explained in Section 2.4. In addition to the $P-v$ and $T-v$ diagrams, the 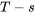$T-s$ diagram is commonly used to illustrate the relation between temperature and specific entropy of a pure substance. Figure 6.7.1 shows the 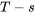$T-s$ diagram for water.

Example 1

Fill in the table.

Substance	T, ^oC	P, kPa	v, m³/kg	Quality x	s, kJ/kg-K	Phase
Water	250		0.02
R134a	-2	100

Solution:

Water: T = 250 ^oC, 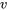$v$ = 0.2 m³/kg

From Table A1: T = 250 ^oC, 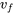$v_f$ = 0.001252 m³/kg, 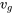$v_g$ = 0.050083 m³/kg

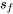Since $v_f < v < v_g$ , water at the given state is a two phase mixture; the saturation pressure is P_sat = 3976.17 kPa, and $s_f$ = 2.7935 kJ/kgK, 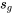$s_g$ = 6.0721 kJ/kgK

The quality is

\[x = \dfrac{v - v_f}{v_{g} - v_{f}} = \dfrac{0.02 - 0.001252}{0.050083 - 0.001252} = 0.383936\]

The specific entropy is

$\text{[math]}$

R134a: T = -2 ^oC, P = 100 kPa

From Table C1: by examining the saturation pressures at 0 ^oC and – 5 ^oC, we can estimate that the saturation pressure for T = -2 ^oC is about 270 kPa; therefore, R134a at the given state is a superheated vapour.

From Table C2,

\[s\]

\[\because \dfrac{v - 0.207433}{0.2160303 - 0.207433} = \dfrac{s - 1.7986}{1.8288 - 1.7986} = \dfrac{-2 - (-10)}{0 - (-10)}\]

$5262d9b134755376bc28996ffe5c05f1.png$ and $397f45d0c2ae3f5307ca1545acfd5e99.png$

In summary,

Substance	T ^oC	P kPa	v m³/kg	Quality x	s kJ/kg-K	Phase
Water	250	3976.17	0.02	0.383936	4.0523	two-phase
R134a	-2	100	0.214529	n.a.	1.8228	superheated vapour

Example 2

A rigid tank contains 3 kg of R134a initially at 0^oC, 200 kPa. R134a is now cooled until its temperature drops to -20^oC. Determine the change in entropy, 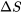$\Delta S$ , of R134a during this process. Is $\Delta S=S_{gen}$ ?

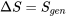Solution:

The initial state is at T₁ = 0^oC and P₁ =200 kPa. From Table C2 in Appendix C,

\[s_1\]

The tank is rigid; therefore, 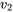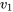$v_2$ = $v_1$ = 0.104811 m³/kg.

From Table C1, at T₂ = -20^oC:

\[v_f\]

\[s_f\]

Because $v_f < v_2 < v_g$ , the final state is a two-phase mixture.

\[x_2 = \dfrac{v_2 - v_f}{v_g-v_f} = \dfrac{0.104811 - 0.000736}{0.147395-0.000736}=0.70964\]

$\text{[math]}$

The total entropy change is

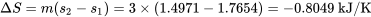
$2bd3eb152634e450850e1eed9c4c7bf1.png$

It is important to note that $\Delta S \neq S_{gen}$ in general. The total entropy of R134a decreases in this cooling process, but the entropy generation is always greater than zero in a real process.

6.7.2 Determining the specific entropy of solids and liquids

The specific entropy of a solid or a liquid depends mainly on the temperature. The change of specific entropy in a process from states 1 to 2 can be calculated as,

\[s_2-s_1=C_pln\dfrac{T_2}{T_1}\]

where

\[s\]

\[C_p\]

\[T\]

6.7.3 Determining the specific entropy of ideal gases

The specific entropy of an ideal gas is a function of both temperature and pressure. Here we will introduce a simplified method for calculating the change of the specific entropy of an ideal gas in a process by assuming constant specific heats. This method is reasonably accurate for a process undergoing a small temperature change.

\[s_2-s_1=C_pln\displaystyle\frac{T_2}{T_1}-Rln\frac{P_2}{P_1}\]

\[s_2-s_1=C_vln\displaystyle\frac{T_2}{T_1}+Rln\frac{v_2}{v_1}\]

where

\[C_p\]

\[T\]

\[P\]

\[s\]

\[v\]

Example 3

Air is compressed from an initial state of 100 kPa, 27^oC to a final state of 600 kPa, 67^oC. Treat air as an ideal gas. Calculate the change of specific entropy, 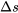$\Delta s$ , in this process. Is $\Delta s = s_{gen}$ ?

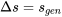Solution:

From Table G1: C_p = 1.005 kJ/kgK, R = 0.287 kJ/kgK

$\text{[math]}$

It is important to note that $\Delta s \neq s_{gen}$ in general. The specific entropy decreases in this process, but the rate of entropy generation is always greater than zero in a real process.

6.7.4 Isentropic relations for an ideal gas

If a process is reversible and adiabatic, it is called an isentropic process and its entropy remains constant. An isentropic process is an idealized process. It is commonly used as a basis for evaluating real processes. The concept of isentropic applies to all substances including ideal gases. The following isentropic relations, however, are ONLY valid for ideal gases.

\[Pv^k= \rm{constant}\]

where

\[k=\dfrac{C_p}{C_v}\]

\[T\]

\[P\]

\[v\]

It is noted that the isentropic relation 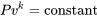$Pv^k = \rm{constant}$ for ideal gases is actually a special case of the polytropic relation 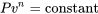$Pv^n = \rm{constant}$ with $n = k = \dfrac{C_p}{C_v}$ .

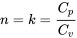Example 4

Derive the isentropic relation 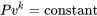$Pv^k= \rm{constant}$

Solution:

For an ideal gas undergoing an isentropic process,

\[\Delta s = s_2 - s_1 =C_pln\displaystyle\frac{T_2}{T_1}-Rln\frac{P_2}{P_1}=0\]

Substitute 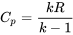$C_p = \dfrac{kR}{k-1}$ in the above equation and rearrange,

\[\because \dfrac{k}{k-1}ln\dfrac{T_2}{T_1} = ln\dfrac{P_2}{P_1}\]

\[\therefore ln\left(\dfrac{T_2}{T_1}\right)^{\dfrac{k}{k-1}} = ln\dfrac{P_2}{P_1}\]

\[\therefore \dfrac{P_2}{P_1} = \left(\dfrac{T_2}{T_1}\right)^{\dfrac{k}{k-1}}\]

Combine with the ideal gas law, 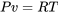$Pv = RT$ ,

\[\therefore \dfrac{P_2}{P_1} = \left(\dfrac{T_2}{T_1}\right)^{\dfrac{k}{k-1}} = \left(\dfrac{P_{2}v_{2}}{P_{1}v_{1}}\right)^{\dfrac{k}{k-1}}\]

\[\therefore \dfrac{P_2}{P_1} = \left(\dfrac{v_1}{v_2}\right)^k\]

\[\therefore Pv^k = \rm{constant}\]

Query $\PageIndex{1}$

Search

Media Attributions