4.1: Statically Equivalent Systems
- Page ID
- 50585
Two sets of forces are considered statically equivalent if they cause the same set of reaction forces on a body. Because this is true, the two statically equivalent sets of forces are interchangeable in statics analysis.
Determining if Forces are Statically Equivalent:
To determine if two sets of forces are statically equivalent, you must solve for the reaction forces in both cases. If the reaction forces are the same then the two sets of forces must be statically equivalent. For any one set of forces, there are an infinite number of sets of forces that are statically equivalent to original set of forces.
Finding a Single Equivalent Point Force:
In statics analysis, we are usually looking to simplify a problem by turning multiple forces into a single, statically equivalent force. To find a single point force that is equivalent to multiple point forces you can use the following procedure.
- Solve for the reaction forces in the original scenario.
- Draw a new free body diagram with these reaction forces. You will also add one force with an unknown magnitude, direction, and point of application to your diagram. This is the single point load that will be equivalent to your original set of forces.
- Write out the equations of equilibrium for this scenario, including the known values for the reaction forces.
- First, solve the force equations to find the \(x\) and \(y\) components of this unknown force (or \(x\), \(y\) and \(z\) components for a 3D problem). This can be used to find the magnitude and direction of the statically equivalent point force.
- Next, use the moment equation (or equations, for 3D problems) to determine the location of the statically equivalent point force.
Example \(\PageIndex{1}\)
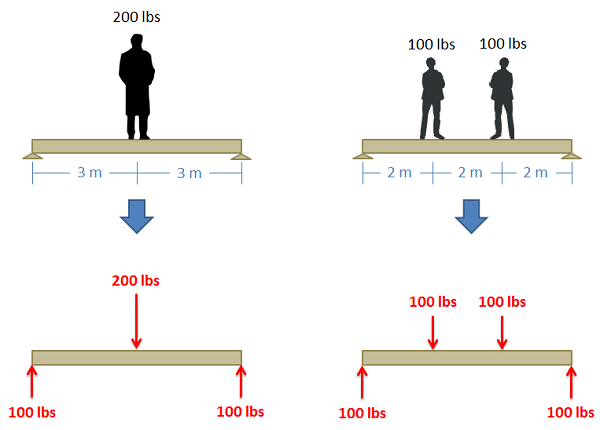
Determine if the two sets of forces shown below are statically equivalent.

- Solution
-
Video \(\PageIndex{2}\): worked solution to example problem \(\PageIndex{1}\), provided by Dr. Jacob Moore. YouTube source: https://youtu.be/Xv5DyvQD29E.


