4.2: Resolution of a Force into a Force and a Couple
- Page ID
- 50586
As discussed on the sections on moments, a force can have a tendency to cause both a linear and angular acceleration. For example, below is diagram of a force acting on an extended body. If we were to think about everything relative to the center of mass of this body, there would be some force acting on the center of mass that would cause the same linear acceleration and some pure moment (couple) that would cause the same angular acceleration. This would be a force and couple that is statically equivalent to the original force, though the point of application of the force changes.
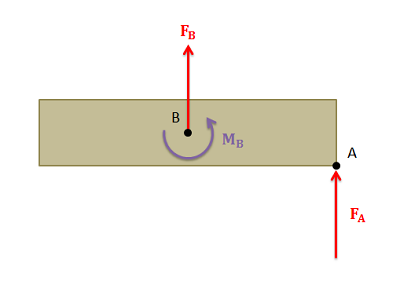
The process of transforming one force applied at one point, into a force and a couple at some other point is known as resolving a force into a force and a couple. There are a few reasons that we may want to do this, but one primary reason is to find the equivalent force couple system for a complex set of forces and moments. The equivalent force couple system is used to simplify more complex analysis, and consists of a single force and a single pure moment (couple) that are statically equivalent to some more complex combination of forces and moments. An important first step in finding the equivalent force couple system is to resolve all the forces so that everything is acting at the same point.
In order to visualize the process of resolving a force into a force and a couple, you can use the process outlined in the diagram below. Imagine we have a body with a force acting at some point A. We want to resolve the force into a force and a couple about some other point B. To do this we will first add two forces to the diagram at point B. One will have the same magnitude and direction as the original force and the other will be equal and opposite to the original force. Because these two forces are equal, opposite, and collinear, this will not change the situation (it's the equivalent to adding zero to an equation). Now, with these three forces acting on the diagram, we can break it down into two sets. The first is a force acting at point B with the same magnitude and direction as the original force. The other two forces act as a couple, exerting a pure moment about point B. Finally, we can redraw the system as a force acting at point B and the pure moment acting about point B.
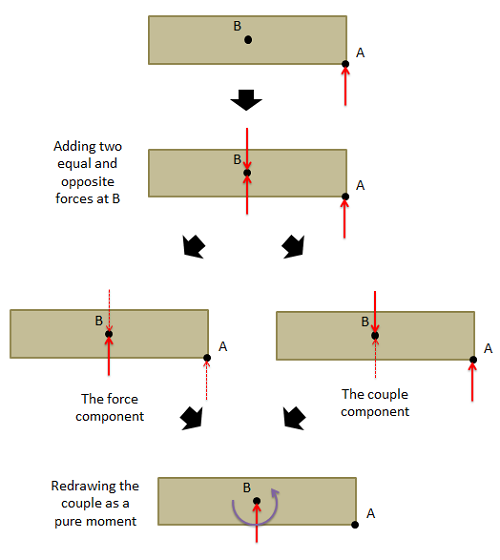
As a shortcut to the process described above, we can also see that the force in the equivalent force couple system will always have a magnitude and direction equal to the original force and the couple will be equal to the moment exerted by the original force about the new point of application.
Example \(\PageIndex{1}\)
Resolve the force shown below to a force and a couple acting at point A.

- Solution
-
Video \(\PageIndex{2}\): Worked solution to example problem \(\PageIndex{1}\), provided by Dr. Jacob Moore. YouTube source: https://youtu.be/Wfl3S_5FD0Q.
Example \(\PageIndex{2}\)
Resolve the force shown below to a force and a couple acting at point A.

- Solution
-
Video \(\PageIndex{3}\): Worked solution to example problem \(\PageIndex{2}\), provided by Dr. Jacob Moore. YouTube source: https://youtu.be/1hRrKhWzf98.


