4.3: Equivalent Force Couple System

Last updated
Save as PDF

Page ID: 50587

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Every set of forces and moments has an equivalent force couple system. This is a single force and pure moment (couple) acting at a single point that is statically equivalent to the original set of forces and moments.

On the left, a set of forces acts upon different points of a rectangular body: downwards on the top left corner, leftwards at the top right corner, upwards at the center of mass and the bottom right corner, and upwards and to the right at the bottom left corner. This system is equivalent to the one drawn on the right, consisting of the same rectangular body experiencing a force pointing upwards and to the left at the center of mass, with a larger magnitude than any of the individual forces in the diagram on the left, and a counterclockwise moment about the center of mass. — Figure \(\PageIndex{1}\): Any set of forces on a body can be replaced by a single force and a single couple acting that is statically equivalent to the original set of forces and moments. This set of an equivalent force and a couple is known as the equivalent force couple system.

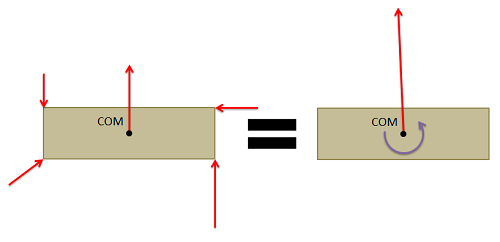
To find the equivalent force couple system, you simply need to follow the steps below.

First, choose a point to take the equivalent force couple system about. Any point will work, but the point you choose will affect the final values you find for the equivalent force couple system. Traditionally, this point will either be the center of mass of the body or some connection point for the body.
Next, resolve all the forces not acting though that point to a force and a couple acting at the point you chose.
To find the "force" part of the equivalent force couple system, add together all the force vectors. This will give you the magnitude and the direction of the force in the equivalent force couple system.
To find the "couple" part of the equivalent force couple system, add together any moment vectors (this could be moments originally acting on the body, or moments from the resolution of the forces into forces and couples). This will give you the magnitude and direction of the pure moment (couple) in the equivalent force couple system.

Video lecture covering this section, delivered by Dr. Jacob Moore. YouTube source: https://youtu.be/bs6Tnlje3IU.

Example \(\PageIndex{1}\)

Find the equivalent force couple system for the forces shown below about point A.

Two bars are connected to form an L-shape, with point A (at the lower left corner of the part) marking the intersection of the vertical and horizontal arms. The vertical arm is 1.5 meters long, and experiences a rightwards force of magnitude 50 N and a counterclockwise moment of magnitude 100 Newton-meters. 0.5 meters to the right of A, a downards force of 40 N is applied to the horizontal arm of the L; 1.5 meters to the right of that, a downwards force of 60 N is applied to the horiztonal arm. — Figure \(\PageIndex{2}\): problem diagram for Example \(\PageIndex{1}\). An L-shaped part whose two arms connect at point A experiences a rightwards force and a counterclockwise moment about the end of its vertical arm, as well as two downwards forces along its horizontal arm.

Solution: Video \(\PageIndex{2}\): Worked solution to example problem \(\PageIndex{1}\), provided by Dr. Jacob Moore. YouTube source: https://youtu.be/cw-rwBZef5w.