Skip to main content
Engineering LibreTexts

10.6: Chapter 10 Homework Problems

  1. Last updated
  2. Save as PDF
  • Page ID
    54748

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    Exercise \(\PageIndex{1}\)

    A jackhammer exerts the impulse shown below on the 1.5-kilogram bit to drive it towards the ground. If the bit starts at rest, what will the expected velocity of the bit be at the end of the impulse?

    Graph of the force in kiloNewtons exerted by a jackhammer on the jackhammer bit, as a function of time in milliseconds. At t=0, force = 60 kN; the force linearly decreases to a value of 30 kN at t = 3 ms.
    Figure \(\PageIndex{1}\): problem diagram for Exercise \(\PageIndex{1}\). Graph of the force exerted by the jackhammer on its bit as a function of time.
    Solution

    \(v = 90 \, m/s\)

    Exercise \(\PageIndex{2}\)

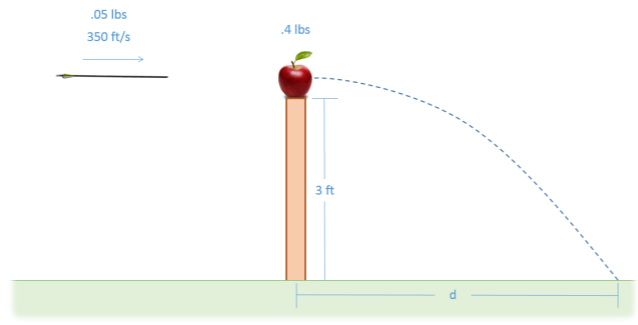
    A 0.05-lb arrow traveling at 350 ft/s impacts a 0.4-lb apple on the top of a post that is 3 feet tall. If the arrow becomes lodged in the apple, how far would we expect the apple to travel \((d)\) before hitting the ground?

    An apple sits on the top of a vertical post at the center of the image. To the left of the post, an arrow is shown flying directly towards the apple. To the right, a dotted line traces the expected path the apple and arrow will take as they fall off the post together. The horizontal distance between the post and the point where these objects will hit the ground is labeled as d.
    Figure \(\PageIndex{2}\): problem diagram for Exercise \(\PageIndex{2}\). An arrow is about to hit an apple; the two will fall together off the pole where the apple is balanced.
    Solution

    \(d = 16.8 \, ft\)

    Exercise \(\PageIndex{3}\)

    A basketball impacts a metal surface as shown below. If the initial velocity of the basketball was 3 ft/s straight down and the coefficient of restitution is 0.85, what is the expected speed and direction \((\theta)\) of the ball after the impact?

    Side view of a metal plate that is tilted so its right end is lower than its left, making a 25° angle above the horizontal. A basketball falls straight down onto the plate, moving towards the right and upwards when it bounces off. The velocity vector of the ball after the collision is an angle of theta above the horizontal.
    Figure \(\PageIndex{3}\): problem diagram for Exercise \(\PageIndex{3}\). A basketball falls onto a metal surface tilted at 25° from the horizontal, bouncing off at some speed at an angle of \(\theta\) from the horizontal.
    Solution

    \(v = 2.64 \, ft, \, \theta = 36.25°\)

    Exercise \(\PageIndex{4}\)

    Puck A, traveling with an initial velocity of 5 m/s, strikes the stationary Puck B. Assuming the collision is elastic, what will the velocity of each puck be immediately after the collision?

    The 2-kg Puck B is stationary in the lower left of the image. The 4-kg Puck A is slightly above and to the right of Puck B, moving to the left at 5 m/s, and has just collided with the edge of Puck B. The edge of their plane of contact is a diagonal line 45° from the horizontal, stretching from the upper left of the image to the lower right. The tangential axis of the problem is along this edge of the plane of contact, pointing to the upper left. The normal axis, pointing to the upper right, is 90° clockwise from this tangential axis.
    Figure \(\PageIndex{4}\): problem diagram for Exercise \(\PageIndex{4}\). Puck A moves towards the left, striking the upper right corner of Puck B and creating a plane of contact that translates to a tangential axis 45° from the horizontal.
    Solution

    \(\vec{v}_{A, f} = [-3.34, 1.67] \, m/s \)

    \(\vec{v}_{B, f} = [-3.34, -3.34] \, m/s \)

    Exercise \(\PageIndex{5}\)

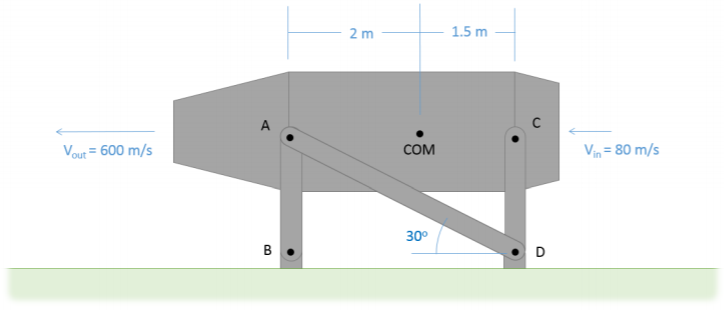
    A jet engine with a mass of 700 kg and an air mass flow rate of 50 kg/s is mounted to a stand as shown below (a set of legs on each side, only one half shown). Based on the input and output velocities shown below, determine the thrust force of the engine and the forces in stand members \(AB\), \(AD\), and \(CD\). Be sure to indicate if each member is in tension or compression.

    Side view of a jet engine, with the wider input side on the right and the narrower output side on the left. The input air velocity is 80 m/s, and the output velocity is 600 m/s. The engine's center of mass is indicated. AB, one vertical leg of the stand the engine is mounted on, is 2 meters to the left of the center of mass, and CD, another vertical leg of the stand, is located 1.5 meters to the right of the center of mass. The member AD connects the top of leg AB to the bottom of leg CD, running at a 30° angle from the horizontal.
    Figure \(\PageIndex{5}\): problem diagram for Exercise \(\PageIndex{5}\). A jet engine facing towards the left is mounted on a stand consisting of 4 legs, two on the side of the engine facing the viewer and two on the opposite side, with a single diagonal member connecting the legs within each set.
    Solution

    \(F_{thrust} = 26 \, kN\)

    \(F_{AB} = 6.04 \, kN \, T\)

    \(F_{AD} = 15.01 \, kN \, C\)

    \(F_{CD} = 1.96 \, kN \, C\)

    This page titled 10.6: Chapter 10 Homework Problems is shared under a CC BY-SA 4.0 license and was authored, remixed, and/or curated by Jacob Moore & Contributors (Mechanics Map) via source content that was edited to the style and standards of the LibreTexts platform.

    1. Back to top
    • Was this article helpful?

    Recommended articles

    1. Article type
      Section or Page
      Author
      Jacob Moore & Contributors
      License
      CC BY-SA
      License Version
      4.0
      Show TOC
      no
    2. Tags
      1. source@http://mechanicsmap.psu.edu