7.2: Equivalence of the Minimum Potential Energy and Principle of Virtual Work
- Page ID
- 21512
The concept of virtual displacement \(\delta u_i\) is the backbone of the energy methods in mechanics. The virtual displacement is a small hypothetical displacement which satisfy the kinematic boundary condition. The virtual strains \(\delta \epsilon_{ij}\) are obtained from the virtual displacement by
\[\delta \epsilon_{ij} = \frac{1}{2} (\delta u_{i,j} + \delta u_{j,i})\]
The increment of stress \(\delta \sigma_{ij}\) corresponding to the increment of strain is obtained from the elasticity law
\[\sigma_{ij} = C_{ijkl}\epsilon_{kl}\]
\[\delta \sigma_{ij} = C_{ijkl}\delta \epsilon_{kl}\]
Therefore, by eliminating \(C_{ijkl}\)
\[\sigma_{ij} \delta \epsilon_{ij} = \epsilon_{ij}\delta \sigma_{ij} \label{8.15}\]
The total strain energy of the elastic system \(\prod\) is the sum of the elastic strain energy stored and the work of external forces
\[\prod = \int_{V} \frac{1}{2} \sigma_{ij} \epsilon_{ij} dv − \int_{S} T_iu_i ds \]
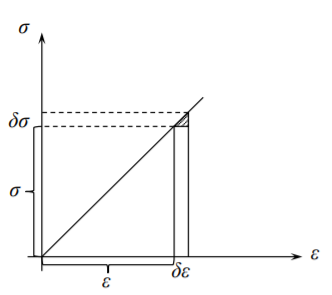
In the above equation the surface traction are given and considered to be constant. The stresses \(\sigma_{ij}\) are not considered to be constant because they are related to the variable strains. For equilibrium the potential energy must be stationary, \(\delta \prod = 0\) or
\[\delta \int_{V} \frac{1}{2} \sigma_{ij} \epsilon_{ij} dv − \delta \int_{S} T_i u_i ds \\ = \frac{1}{2} \int_{V} \delta (\sigma_{ij} \epsilon_{ij}) dv − \int_{S} T_i \delta u_i ds \\ = \frac{1}{2} \int_{V} (\delta \sigma_{ij} \epsilon_{ij} + \sigma_{ij} \delta \epsilon_{ij}) dv − \int_{S} T_i \delta u_i ds = 0 \label{8.17}\]
The two terms in the integrand of the volume integral are equal in view of Equation \ref{8.15}. Therefore, Equation \ref{8.17} can be written in the equivalent form
\[\int_{V} \sigma_{ij} \delta \epsilon_{ij} dv = \int_{S} T_i \delta u_i ds \]
which is precisely the principle of virtual work. The above proof goes also in the opposite direction. Assuming the principle of virtual work one can show that the stationarity of the total potential energy holds.


