1.10:Exercises

Last updated
Save as PDF

Page ID: 52875

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Analysis

1. A 2000 count digital multimeter has an accuracy specification of $\pm$1%. If it reads a voltage of 34.2 volts, what is the possible range of the true voltage?

Answer 1

33.858V to 34.542V

2. Determine the expected voltage scales for a standard “three and a half” digit meter between 1 and 1000 volts.

Answer 2

2 Volt, 20Volt, and 200 Volt scales

4. Determine the expected current scales for a standard “three and a half” digit meter between 1 mA and 1 amp.

5. A 2000 count digital multimeter has an accuracy specification of $\pm$2% and $\pm$5 counts. If it reads a voltage of 7.00 volts, what is the possible range of the true voltage?

Answer 5

6.81V to 7.19V

6. A 50000 count digital multimeter has an accuracy specification of $\pm$0.1% and $\pm$4 counts. If it reads a voltage of 7.00 volts, what is the possible range of the true voltage?

7. What is the charge in coulombs of a million million ($10^{12}$) electrons?

Answer 7

$1.602 \times 10^{-7} Coulombs$

8. What is the charge in coulombs of $10^{15}$ electrons?

9. How many electrons would be needed for a charge of 20 coulombs?

Answer 9

$1.248 \times 10^{20} electrons$

10. How many electrons would be needed for a charge of 1 microcoulomb?

11. If a charge of 2 coulombs passes through a wire in 5 seconds, what is the current?

Answer 11

0.4 Amps

12. If a charge of 300 millicoulombs passes through a wire in 0.1 seconds, what is the current?

13. How much charge must be transferred in 0.1 seconds in order to achieve a current of 5 amps?

Answer 13

0.5 Coulombs

14. How much charge must be transferred in 20 seconds in order to achieve a current of 10 microamps?

15. Determine the resulting voltage if it takes 2 joules to move 10 coulombs of charge.

Answer 15

0.2 Volts

16. Determine the voltage if 15 joules is used to move 0.5 coulombs of charge.

17. How much energy is required to create a 10 volt potential difference with a 2 coulomb charge?

Answer 17

20 Joules

18. How much energy is required to create a 50 millivolt potential difference with a 0.1 coulomb charge?

19. What is the wattage equivalent of two horsepower (2 hp)?

Answer 19

1492 Watts

20. What is the horsepower equivalent of 1000 watts?

21. If a device draws 2 amps of current from a 12 volt battery, determine the power delivered.

Answer 21

24 Watts

22. If a device draws 10 milliamps of current from a 1.5 volt battery, determine the power delivered.

23. A 2 hp motor draws 1800 watts from its source. Determine its efficiency.

Answer 23

82.9%

24. A 5 hp motor draws 4.5 kw from its source. Determine its efficiency.

25. An audio power amplifier is rated for 500 watts of maximum audio output at an efficiency of 80%. Determine the amount of wasted power.

Answer 25

125 Watts

26. A compressor draws 10 amps of current from a 120 volt source. Its rated output is 1 hp. Determine the efficiency.

27. An application requires a battery to deliver 15 mA for at least 200 hours. Determine the required amp-hour rating (assume the battery can supply 100% of its energy).

Answer 27

3Ah

28. Determine the required rating for a battery to deliver 0.8 A for at least 30 hours.

29. A certain 12 volt battery has a rating of 6 Ah. Determine the expected battery life using a 5 mA draw. Assume 100% energy usage.

Answer 29

1200 hours

30. A certain AA battery has a rating of 800 mAh. Determine the expected battery life using a 20 mA draw.

31. Assume that a certain piece of material has a resistance of 80 ohms. Determine the new resistance if the length of the piece is doubled and no other parameters are changed.

Answer 31

$160 \Omega$

32. Assume that a certain piece of material has a resistance of 2 k ohms. Determine the new resistance if the width and height of the piece are doubled and no other parameters are changed.

33. Assume that a certain piece of material has a resistance of 4 ohms. Determine the new resistance if the resistivity is doubled and no other parameters are changed.

Answer 33

$8 \Omega$

34. Assume that a certain piece of material has a resistance of 10 k ohms. Determine the new resistance if the length, width and height of the piece are all halved.

35. A certain material has a resistivity of 100 ohm-centimeters. Determine the resistance of a piece that is 1 cm wide, 0.5 cm high and 6 cm long.

Answer 35

$1200 \Omega$

36. A certain material has a resistivity of 2000 ohm-centimeters. Determine the resistance of a piece that is 2 mm wide, 4 mm high and 10 mm long.

37. A 40 ohm resistor has dimension of 0.4 cm wide by 0.2 cm high by 1 cm long. Determine the resistivity in ohm-centimeters.

Answer 37

$3.2 \Omega \cdot cm $

38. A 5000 ohm resistor has dimension of 5 mm wide by 3 mm high by 6 mm long. Determine the resistivity in ohm-centimeters.

39. A resistor with the color code yellow-violet-red-silver has a measured value of 4806 ohms. Is this resistor within tolerance? As a percentage, how far is it from the nominal value?

Answer 39

yes, +2.26%

40. A resistor with the color code orange-orange-yellow-gold has a measured value of 33.9 k ohms. Is this resistor within tolerance? As a percentage, how far is it from the nominal value?

41. A resistor with the color code brown-black-orange-silver has a measured value of 9980 ohms. Is this resistor within tolerance? As a percentage, how far is it from the nominal value?

Answer 41

yes, -0.2%

42. A resistor with the color code green-blue-black-gold has a measured value of 50 ohms. Is this resistor within tolerance? As a percentage, how far is it from the nominal value?

43. Determine the value of the resistors pictured in Figure 1.10.1 (left-to-right: red-black-yellow, blue-gray-orange, red-violet-red-silver).

Answer 43

$200 k\Omega, 68 k\Omega, 2.7 k\Omega$

44. Determine the value of the resistors pictured in Figure 1.10.2 (left-to-right: red-red-orange-gold, brown-black-red-gold, yellow-violet-orange-silver).

45. Determine the value of the resistors pictured in Figure 1.10.3 (left-to-right: orange-orange-green-silver, white-brown-black-silver, orange-white-brown-gold).

Answer 45

$3.3 M\Omega, 91\Omega, 390\Omega$

46. Determine the value of the resistors pictured in Figure 1.10.4 (left-to-right: silver-orange-violet-yellow, green-blue-yellow-gold, gold-black-orange-yellow).

47. Determine the maximum and minimum allowed values of the resistors pictured in Figure 1.10.1 .

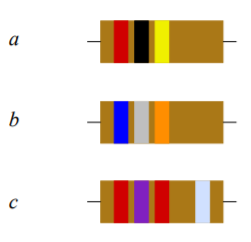
2.42.png

Figure 1.10.1

Answer 47

160k to 240k
54.4k to 81.6k
2.43k to 2.97k

48. Determine the maximum and minimum allowed values of the resistors pictured in Figure 1.10.2 .

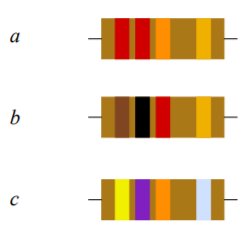
2.43.png

Figure 1.10.2

49. Determine the maximum and minimum allowed values of the resistors pictured in Figure 1.10.3 .

2.44.png

Figure 1.10.3

Answer 49

2.97M to 3.63M
81.9 to 100.1
370.5 to 409.5

50. Determine the maximum and minimum allowed values of the resistors pictured in Figure 1.10.4 .

2.45.png

Figure 1.10.4

Design

51. Determine the resistor color code for the following ohmic values using 5% tolerance:

a) 47 $\Omega$

b) 22 k$\Omega$

c) 390 k$\Omega$

d) 2.2 k$\Omega$

e) 560 $\Omega$

Answer 51

yellow-violet-black-gold
Red-red-orange-gold
orange-white-yellow-gold
brown-red-oragne-gold
violet-green-brown-gold

52. Determine the resistor color code for the following ohmic values using 10% tolerance:

a) 56 $\Omega$

b) 33 k$\Omega$

c) 470 k$\Omega$

d) 1.2 k$\Omega$e) 750 $\Omega$

Challenge

53. A radio transmitter is rated for 100 watts of maximum output at an efficiency of 90%. If it is fed from a 120 volt source, determine the current draw.

Answer 53

Input power: $frac{100 W}{0.9} = 111.11 W$
Current: $I = frac{P}{V} = frac{111.11}{120}=0.93A$

54. A certain 75 watt incandescent bulb produces 71 watts worth of heat and the remainder in the form of light. Determine its efficiency as a lighting device and its efficiency as a heating device.

55. Assume it takes an 1800 watt toaster 3 minutes to toast a bagel “just right”. If you toast a bagel every morning for a year and electricity costs 15 cents/kWh, how much will you have spent in that year to toast bagels?

Answer 55

Minutes/year = $3 \times 365 = 1095 \: minutes$
Hours/year = $1095 \: minutes \times \frac{1 hour}{60 minutes} = 18.25 \: hours$
Energy = $1.8kW \times 18.25 \: hours = 32.85kWh$
Cost = $32.85kWh \times 15 \frac{cents}{kWh}+ = $4.93$

56. Assume that you can buy standard 60 watt incandescent light bulbs for 50 cents each and that each has an expected life span of 1000 hours. In comparison, you can buy an LED light bulb that produces the same amount of light but only consumes 7 watts. The LED bulbs cost $5.50 each and have an expected life of 20,000 hours. Assuming electricity costs 14 cents/kWh, determine the total cost of running incandescent lights versus LEDs for 40,000 hours.

57. Given a 1.5 volt battery with a 500 mAh rating, how much current can it produce continuously for 25 hours?.

58. Given a 9 volt battery with a 100 mAh rating, determine the total energy storage in joules.

59. A 2000 count DMM with $\pm$1% accuracy is used to measure the resistance of a spool of AWG 22 wire. If the measurement is 4.50 $\Omega$, determine the length of the wire and the possible inaccuracy (in feet or meters).

60. A length of AWG 26 wire is attached to one end of a length of AWG 32 wire. The total length of the two wires is 200 meters. Determine the length and resistance of each piece if the total resistance is 75 $\Omega$.

Search

Text Color

Text Size

Margin Size

Font Type