8.5: Nested For Loops

Last updated
Save as PDF

Page ID: 29081

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

General Discussion

Nested Control Structures

We have looked at nested if statements in prior lesson, where one conditional statement was nested within the code black of another if statement. For example:

if age is less than 18
  you can't vote
  if age is less than 16
    you can't drive
  else
    you can drive
else
  you can vote
  if age is less than 21
    you can't drink
  else
    you can drink

As you can see we simply included as part of the "true action" a statement and another if then else control structure. We did the same (nested another if then else) for the "false action". In our example we nested if then else control structures. Nesting could have an if then else within a while loop. Thus, the concept of nesting allows the mixing of the different categories of control structures.

Many complex logic problems require using nested control structures. By nesting control structures (or placing one inside another) we can accomplish almost any complex logic problem.

An Example - Nested for loops

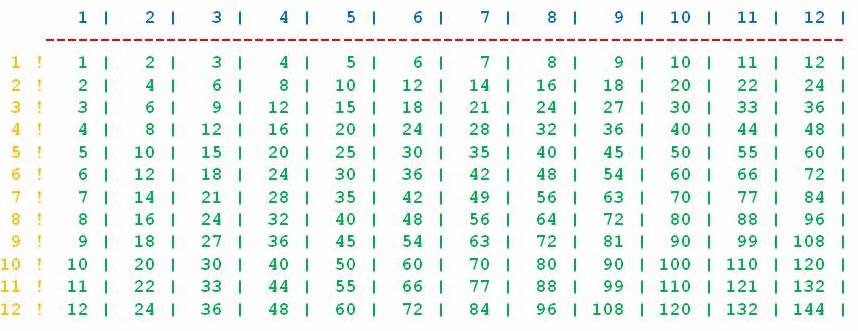
We might also see that the answers could be designed as a collection of cells (each cell being exactly six spaces wide). The C++ source code below shows 4 different loops - the last one is nested inside of another loop. This allows us to process table data by row and column. This also exhibits usage of the setw() function with the cout function.

C++ source code: nested for loops - multiplication table
// Prints the top line of blue numerals 1 through 12 separated by |
cout << "      ";
for(across=1; across <13; across++)
{
  cout << setw(4) << across << " |";
}
cout << endl;

// Prints the red linebelow th eblue numerals
cout << "      ";
for(across=1; across <13; across++)
{
  cout << "------";
}
cout << endl;

// The outer loop prints the yellow numbers down the left side followed by the exclamatin point
for(down=1; down <13; down++)
{
  cout << setw(4) << down << " !";
  // The inner loop prints out the product of each column (down) multiplied be each row (across)
  for(across=1; across <13; across++)
  {
    cout << setw(4) << down*across << " |";
  }
  cout << endl;
}

A multiplication table showing output in rows and columns. — Figure \(\PageIndex{1}\): Colorized Code - multiplication table

Definitions

Complex Logic: Often solved with nested control structures.

Adapted from:
"Nested For Loops" by Kenneth Busbee, Download for free at http://cnx.org/contents/303800f3-07f...93e8948c5@22.2 is licensed under CC BY 4.0