15.2: Plot 3D Surface and Contour Plots

By Carey A. Smith

meshgrid() function

Surface plots need 2-dimensional grids of x and y coordinates. These are made from 1-dimensional vectors of x and y coordinates using the meshgrid() function. The syntax of meshgrid() is:

[x2D, y2D] = meshgrid(x1D,y1D);

Example \(\PageIndex{1}\) Simple meshgrid() Example

x1D = [0, 1, 2 ,3];
y1D = [0, 2, 4];
[x2D, y2D] = meshgrid(x1D,y1D)

Solution

x2D =
0 1 2 3
0 1 2 3
0 1 2 3
y2D =
0 0 0 0
2 2 2 2
4 4 4 4

As can be seen:

The x coordinates are repeated in all the rows.

The x coordinates are repeated in all the columns.

Watch this video about meshgrid. Note that the presenter uses lower case x & y for 1-dimensional values and upper case X & Y for 1-dimensional values. It is not good practice to use variables names that only differ by lower and upper case. Better is to use different name, like x1D, y1D and x2D, y2D. The important part is 0 to 4:20 minutes.

.

mesh() 3D Plot

The mesh() function creates a wire-frame 3-dimensional plot.

Example \(\PageIndex{2}\) mesh() 3D Plot

%% Create a 3D graph of r^2 = x^2 + y^2 over a grid of points
% 1. Set the x and y axis 1D vectors that define this rectangular grid:
x1D = -3 : 0.5 :3; % 1x13 vector
y1D = -2.5: 0.5 :2.5; % 1x11 vector

%% 2. Matlab's meshgrid() function uses these 1D vectors
% to create 2D arrays of x & y at each point of the rectangular grid.
[x2D, y2D] = meshgrid(x1D,y1D);

%% 3. Compute z(x,y) at each point in the grid.
z = x2D.^2 + 1*x2D + y2D.^2 + 2*y2D;

%% mesh(x,y,z) creates a 3D wire frame plot.
figure;
mesh(x2D, y2D, z);
title('mesh(x2D, y2D, Z)');
colormap jet % This selects a colormap
colorbar; % This displays the color scale
xlabel('x') % This identifies x-axis
ylabel('y')
zlabel('z')

Solution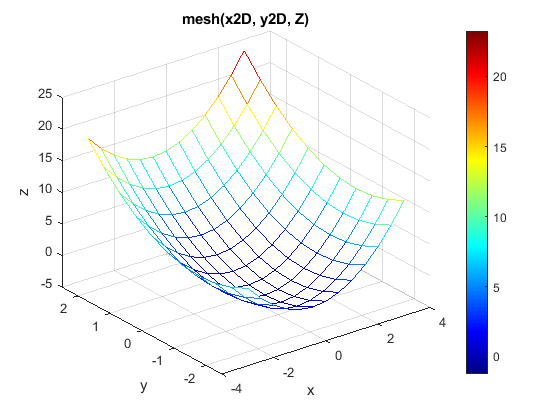

The resulting plot is shown here.

Figure \(\PageIndex{1}\): mesh() 3D plot

.

surf() 3D plot

The surf() function also creates a continous surface 3-dimensional plot. Its usage is the same as the mesh() function.

Example \(\PageIndex{3}\) surf() 3D Plot

format short g; format compact; clear all; close all; clc;

%% Create a 3D graph of r^2 = x^2 + y^2 over a grid of points
% 1. Set the x and y axis 1D vectors that define this rectangular grid:
x1D = -3 : 0.5 :3; % 1x13 vector
y1D = -2.5: 0.5 :2.5; % 1x11 vector

%% 2. Matlab's meshgrid() function uses these 1D vectors
% to create 2D arrays of x & y at each point of the rectangular grid.
[x2D, y2D] = meshgrid(x1D,y1D);

%% 3. Compute z(x,y) at each point in the grid.
z = x2D.^2 + 1*x2D + y2D.^2 + 2*y2D;

%% surf(x,y,z) creates a 3D continous surface plot.
figure;
surf(x2D, y2D, z);
title('mesh(x2D, y2D, Z)');
colormap hot % This selects a colormap
colorbar; % This displays the color scale
xlabel('x') % This identifies x-axis
ylabel('y')
zlabel('z')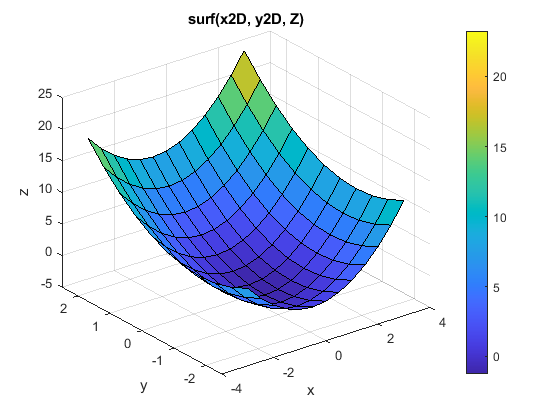

Solution

The resulting plot is shown here.

Figure \(\PageIndex{2}\): surf() 3D plot

See this attached file for images of the colormap options.: colormap_options.pdf

.

contour() Plot

Contour plots are like topographical maps. They display 3D data in a 2D format. The basic syntax is:

contour(x2D, y2D, z);

This can be improved by specifying the contour levels and showing their values:

contour(x2D, y2D, z, levels, 'ShowText','on')); % This creates specified contours and shows their values.

Example \(\PageIndex{4}\) contour() Plot

format short g; format compact; clear all; close all; clc;

%% Create a 3D graph of r^2 = x^2 + y^2 over a grid of points
% 1. Set the x and y axis 1D vectors that define this rectangular grid:
x1D = -3 : 0.5 :3; % 1x13 vector
y1D = -2.5: 0.5 :2.5; % 1x11 vector

%% 2. Matlab's meshgrid() function uses these 1D vectors
% to create 2D arrays of x & y at each point of the rectangular grid.
[x2D, y2D] = meshgrid(x1D,y1D);

%% 3. Compute z(x,y) at each point in the grid.
z = x2D.^2 + 1*x2D + y2D.^2 + 2*y2D;

%% contour(x,y,z) creates a continous surface plot.
figure;
levels = [-4: 2: 24]; % Specify the contours
contour(x2D, y2D, z, levels, 'ShowText','on');
title('contour(x2D, y2D, Z), levels, ''ShowText'',''on'')');
colorbar; % This displays the color scale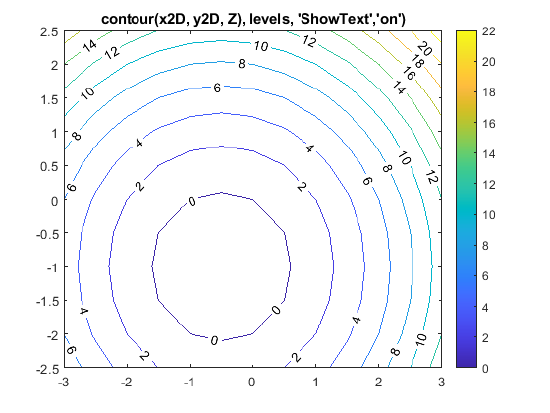

Solution

Resulting plot:

Figure \(\PageIndex{3}\): contour() plot

.

 

 

 

.

colormap Options

jet
parula
hsv
hot
cool
spring
summer
autumn
winter
gray
bone
copper
prism
flag
colorcube
lines