4.6.1.4: Stability of None Systematical or ``Strange'' Bodies
- Page ID
- 691
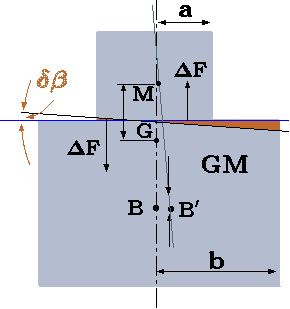
Fig. 4.46. Calculations of \(\overline{GM}\) for abrupt shape body.
While most floating bodies are symmetrical or semi–symmetrical, there are situations where the body has a ``strange'' and/or un-symmetrical body. Consider the first strange body that has an abrupt step change as shown in Figure 4.46. The body weight doesn't change during the rotation that the green area on the left and the green area on right are the same (see Figure 4.46). There are two situations that can occur. After the tilting, the upper part of the body is above the liquid or part of the body is submerged under the water. The mathematical condition for the border is when \(b=3a\). For the case of \(b \lt 3a\) the calculation of moment of inertia are similar to the previous case. The moment created by change in the displaced liquid (area) act in the same fashion as the before. The center of the moment is needed to be found. This point is the intersection of the liquid line with the brown middle line. The moment of inertia should be calculated around this axis. For the case where \(b \lt 3ax\) some part is under the liquid. The amount of area under the liquid section depends on the tilting angle. These calculations are done as if none of the body under the liquid. This point is intersection point liquid with lower body and it is needed to be calculated. The moment of inertia is calculated around this point (note the body is ``ended'' at end of the upper body). However, the moment to return the body is larger than actually was calculated and the bodies tend to be more stable (also for other reasons).
Contributors and Attributions
Dr. Genick Bar-Meir. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or later or Potto license.


