2.1: How to Write a Security Definition
- Page ID
- 7320
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)So far the only form of cryptography we’ve seen is one-time pad, so our discussion of security has been rather specific to one-time pad. It would be preferable to have a vocabulary to talk about security in a more general sense, so that we can ask whether any encryption scheme is secure.
In this section, we’ll develop two security definitions for encryption.
What Doesn’t Go Into a Security Definition
A security definition should give guarantees about what can happen to a system in the presence of an attacker. But not all important properties of a system refer to an attacker. For encryption specifically:
- We don’t reference any attacker when we say that the Enc algorithm takes two arguments (a key and a plaintext), or that the KeyGen algorithm takes no arguments. Specifying the types of inputs/outputs (i.e., the "function signature") of the various algorithms is therefore not a statement about security. We call these properties the syntax of the scheme.
- Even if there is no attacker, it’s still important that decryption is an inverse of encryption. This is not a security property of the encryption scheme. Instead, we call it a correctness property.
Below are the generic definitions for syntax and correctness of symmetric-key encryption:
A symmetric-key encryption (SKE) scheme consists of the following algorithms:
- KeyGen: a randomized algorithm that outputs a key \(k \in \mathcal{K}\).
- Enc: a (possibly randomized) algorithm that takes a key \(k \in \mathcal{K}\) and plaintext \(m \in \mathcal{M}\) as input, and outputs a ciphertext \(c \in C\).
- Dec: a deterministic algorithm that takes a key \(k \in \mathcal{K}\) and ciphertext \(c \in C\) as input, and outputs a plaintext \(m \in \mathcal{M}\).
We call \(\mathcal{K}\) the key space, \(\mathcal{M}\) the message space, and \(C\) the ciphertext space of the scheme. Sometimes we refer to the entire scheme (the collection of all three algorithms) by a single variable \(\sum\). When we do so, we write \(\sum\).KeyGen, \(\sum\).Enc, \(\sum\).Dec, \(\sum . \mathcal{K}, \Sigma\). \(\mathcal{M}\), and \(\sum\). \(\mathcal{C}\) to refer to its components.
An encryption scheme \(\sum\) satisfies correctness if for all \(k \in \Sigma . \mathcal{K}\) and all \(m \in \Sigma . \mathcal{M}\), \[\operatorname{Pr}[\Sigma \cdot \operatorname{Dec}(k, \Sigma . \operatorname{Enc}(k, m))=m]=1\] The definition is written in terms of a probability because Enc is allowed to be a randomized algorithm. In other words, decrypting a ciphertext with the same key that was used for encryption must always result in the original plaintext.
An encryption scheme can have the appropriate syntax but still have degenerate behavior like \(\operatorname{Enc}(k, m)=0^{\lambda}\) (i.e., every plaintext is "encrypted" to \(\theta^{\lambda}\) ). Such a scheme would not satisfy the correctness property.
A different scheme defined by \(\operatorname{Enc}(k, m)=m\) (i.e., the "ciphertext" is always equal to the plaintext itself) and \(\operatorname{Dec}(k, c)=c\) does satisfy the correctness property, but would not satisfy any reasonable security property.
"Real-vs-Random" Style of Security Definition
Let’s try to make a security definition that formalizes the following intuitive idea:
"an encryption scheme is a good one if its ciphertexts look like random junk to an attacker."
Security definitions always consider the attacker’s view of the system. What is the "in terface" that Alice & Bob expose to the attacker by their use of the cryptography, and does that particular interface benefit the attacker?
In this example, we’re considering a scenario where the attacker gets to observe ciphertexts. How exactly are these ciphertexts generated? What are the inputs to Enc (key and plaintext), and how are they chosen?
- Key: It’s hard to imagine any kind of useful security if the attacker knows the key. Hence, we consider that the key is kept secret from the attacker. Of course, the key is generated according to the KeyGen algorithm of the scheme.
At this point in the course, we consider encryption schemes where the key is used to encrypt only one plaintext. Somehow this restriction must be captured in our security definition. Later, we will consider security definitions that consider a key that is used to encrypt many things.
- Plaintext: It turns out to be useful to consider that the attacker actually chooses the plaintexts. This a "pessimistic" choice, since it gives much power to the attacker. However, if the encryption scheme is indeed secure when the attacker chooses the plaintexts, then it’s also secure in more realistic scenarios where the attacker has some uncertainty about the plaintexts.
These clarifications allow us to fill in more specifics about our informal idea of security:
"an encryption scheme is a good one if its ciphertexts look like random junk to an attacker... when each key is secret and used to encrypt only one plaintext, even when the attacker chooses the plaintexts."
A concise way to express all of these details is to consider the attacker as a calling program to the following subroutine:
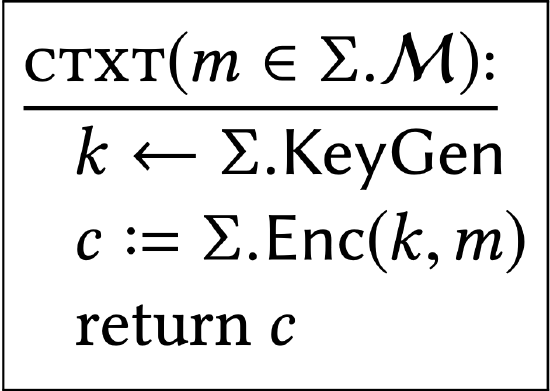
A calling program can choose the argument to the subroutine (in this case, a plaintext), and see only the resulting return value (in this case, a ciphertext). The calling program can’t see values of privately-scoped variables (like \(k\) in this case). If the calling program makes many calls to the subroutine, a fresh key \(k\) is chosen each time.
The interaction between an attacker (calling program) and this \(\texttt{CTXT}\) subroutine appears to capture the relevant scenario. We would like to say that the outputs from the \(\texttt{CTXT}\) subroutine are uniformly distributed. A convenient way of expressing this property is to say that this \(\texttt{CTXT}\) subroutine should have the same effect on every calling program as a \(\texttt{CTXT}\) subroutine that (explicitly) samples its output uniformly.
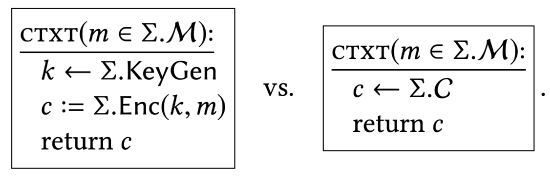
Intuitively, no calling program should have any way of determining which of these two implementations is answering subroutine calls. As an analogy, one way of saying that "\(\texttt{FOO}\) is a correct sorting algorithm" is to say that "no calling program would behave differently if Foo were replaced by an implementation of mergesort."
In summary, we can define security for encryption in the following way:
"an encryption scheme is a good one if, when you plug its KeyGen and Enc algorithms into the template of the \(\texttt{CTXT}\) subroutine above, the two implementations of \(\texttt{CTXT}\) induce identical behavior in every calling program."
In a few pages, we introduce formal notation and definitions for the concepts introduced here. In particular, both the calling program and subroutine can be randomized algorithms, so we should be careful about what we mean by "identical behavior."
One-time pad is defined with KeyGen sampling \(k\) uniformly from \(\{0,1\}^{\lambda}\) and Enc \((k, m)=\) \(k \oplus m\). It satisfies our new security property since, when we plug in this algorithms into the above template, we get the following two subroutine implementations:
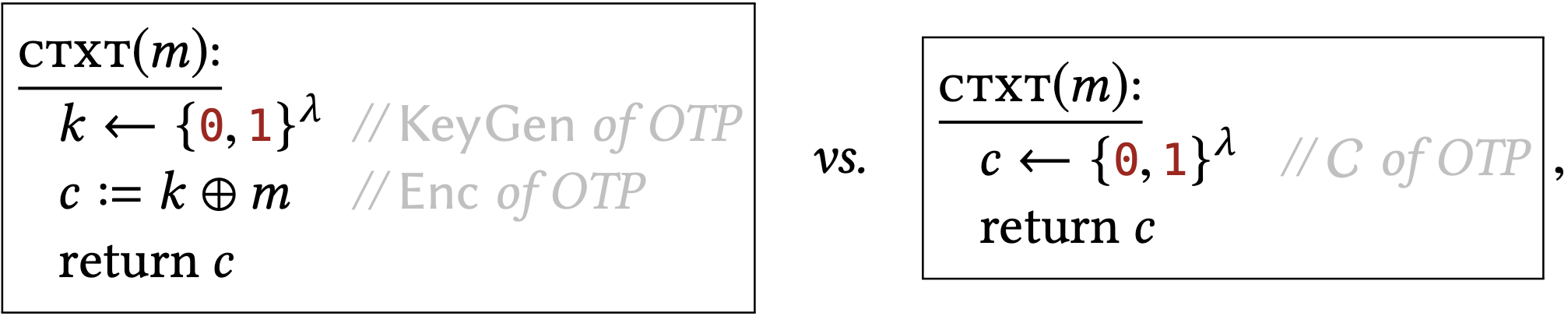
and these two implementations have the same effect on all calling programs.
"Left-vs-Right" Style of Security Definition
Here’s a different intuitive idea of security:
"an encryption scheme is a good one if encryptions of \(m_{L}\) look like encryptions of \(m_{R}\) to an attacker (for all possible \(\left.m_{L}, m_{R}\right)\) ”
As above, we are considering a scenario where the attacker sees some ciphertext(s). These ciphertexts are generated with some key; where does that key come from? These ciphertexts encrypt either some \(m_{L}\) or some \(m_{R}\); where do \(m_{L}\) and \(m_{R}\) come from? We can answer these questions in a similar way as the previous example. Plaintexts \(m_{L}\) and \(m_{R}\) can be chosen by the attacker. The key is chosen according to KeyGen so that it remains secret from the attacker (and is used to generate only one ciphertext).
"an encryption scheme is a good one if encryptions of \(m_{L}\) look like encryptions of \(m_{R}\) to an attacker, when each key is secret and used to encrypt only one plaintext, even when the attacker chooses \(m_{L}\) and \(m_{R} .\)
As before, we formalize this idea by imagining the attacker as a program that calls a particular interface. This time, the attacker will choose two plaintexts \(m_{L}\) and \(m_{R}\), and get a ciphertext in return. \({ }^{2}\) Depending on whether \(m_{L}\) or \(m_{R}\) is actually encrypted, those interfaces are implemented as follows:
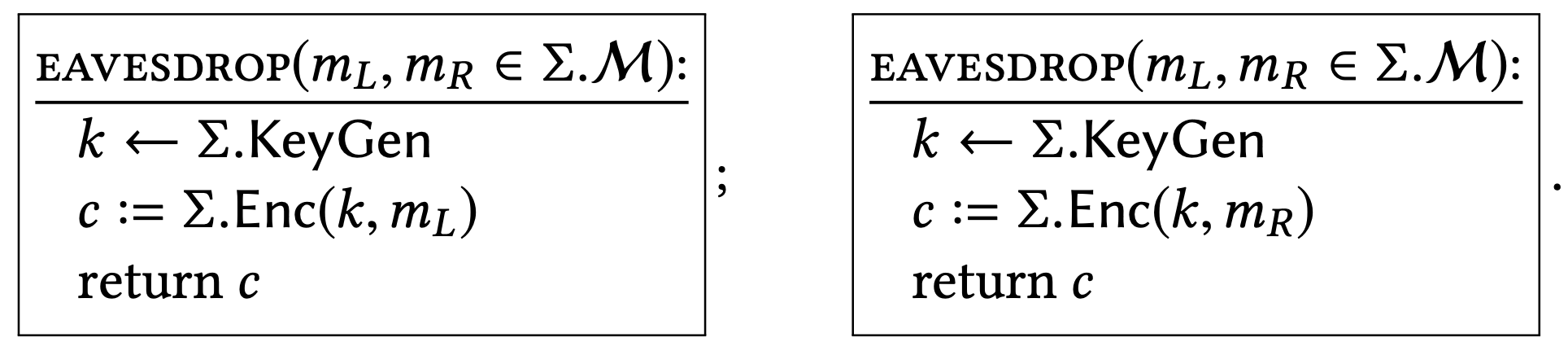
Now the formal way to say that encryptions of \(m_{L}\) "look like" encryptions of \(m_{R}\) is:
"an encryption scheme is a good one if, when you plug its KeyGen and Enc algorithms into the template of the EAVESDROP subroutines above, the two implementations of EAVESDROP induce identical behavior in every calling program."
Does one-time pad satisfy this new security property? To find out, we plug in its algorithms to the above template, and obtain the following implementations:

If these two implementations have the same effect on all calling programs (and indeed they do), then we would say that OTP satisfies this security property.
Is this a better/worse way to define security than the previous way? One security definition considers an attacker whose goal is to distinguish real ciphertexts from random values (real-vs-random paradigm), and the other considers an attacker whose goal is to distinguish real ciphertexts of two different plaintexts (left-vs-right paradigm). Is one "correct" and the other one "incorrect?"We save such discussion until later in the chapter.
\({ }^{2}\) There may be other reasonable ways to formalize this intuitive idea of security. For example, we might choose to give the attacker two ciphertexts instead of one, and demand that the attacker can’t determine which of them encrypts \(m_{L}\) and which encrypts \(m_{R}\). See Exercise \(2.15\).


