2.2: Formalisms for Security Definitions
- Page ID
- 7321
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)So far, we’ve defined security in terms of a single, self-contained subroutine, and imagined the attacker as a program that calls this subroutine. Later in the course we will need to generalize beyond a single subroutine, to a collection of subroutines that share common (private) state information. Staying with the software terminology, we call this collection a library:
A library \(\mathcal{L}\) is a collection of subroutines and private/static variables. A library’s interface consists of the names, argument types, and output type of all of its subroutines (just like a Java interface). If a program \(\mathcal{A}\) includes calls to subroutines in the interface of \(\mathcal{L}\), then we write \(\mathcal{A} \diamond \mathcal{L}\) to denote the result of linking \(\mathcal{A}\) to \(\mathcal{L}\) in the natural way (answering those subroutine calls using the implementation specified in \(\mathcal{L})\). We write \(\mathcal{A} \diamond \mathcal{L} \Rightarrow\) to denote the event that program \(\mathcal{A} \diamond \mathcal{L}\) outputs the value \(z\).
If \(\mathcal{A}\) or \(\mathcal{L}\) is a program that makes random choices, then the output of \(\mathcal{A} \diamond \mathcal{L}\) is a random variable. It is often useful to consider probabilities like \(\operatorname{Pr}[\mathcal{A} \diamond \mathcal{L} \Rightarrow\) true].
Example Here is a familiar library:

And here is one possible calling program:

You can hopefully convince yourself
that \[\operatorname{Pr}[\mathcal{A} \diamond \mathcal{L} \Rightarrow \text { true }]=1 / 2^{\lambda}\]
If this \(\mathcal{A}\) is linked to a different library, its output probability may be different. If a different calling program is linked to this \(\mathcal{L}\), the output probability may be different.
A library can contain several subroutines and private variables that are kept static between subroutine calls. For example, here is a simple library that picks a string s uniformly and allows the calling program to guess \(s\).

Our convention is that code outside of a subroutine (like the first line here) is run once at initialization time. Variables defined at initialization time (like s here) are available in all subroutine scopes (but not to the calling program).
Interchangeability
The idea that "no calling program behaves differently in the presence of these two libraries" still makes sense even for libraries with several subroutines. Since this is such a common concept, we devote new notation to it:
Let \(\mathcal{L}_{\text {left }}\) and \(\mathcal{L}_{\text {right }}\) be two libraries that have the same interface. We say that \(\mathcal{L}_{\text {left }}\) and \(\mathcal{L}_{\text {right }}\) are interchangeable, and write \(\mathcal{L}_{\text {left }} \equiv \mathcal{L}_{\text {right }}\), if for all programs \(\mathcal{A}\) that output a boolean value,
\[\operatorname{Pr}\left[\mathcal{A} \diamond \mathcal{L}_{\text {left }} \Rightarrow \text { true }\right]=\operatorname{Pr}\left[\mathcal{A} \diamond \mathcal{L}_{\text {right }} \Rightarrow \text { true }\right]\]
This definition considers calling programs that give boolean output. Imagine a calling program / attacker whose only goal is to distinguish two particular libraries (indeed, we often refer to the calling program as a distinguisher). A boolean output is enough for that task. You can think of the output bit as the calling program’s "guess" for which library the calling program thinks it is linked to.
The distinction between "calling program outputs true" and "calling program outputs false" is not significant. If two libraries don’t affect the calling program’s probability of outputting true, then they also don’t affect its probability of outputting false:

Here are some very simple and straightforward ways that two libraries may be interchangeable. Hopefully it’s clear that each pair of libraries has identical behavior, and therefore identical effect on all calling programs.
Despite being very simple examples, each of these concepts shows up as a building block in a real security proof in this book.
 |
Their only difference happens in an unreachable block of code. |
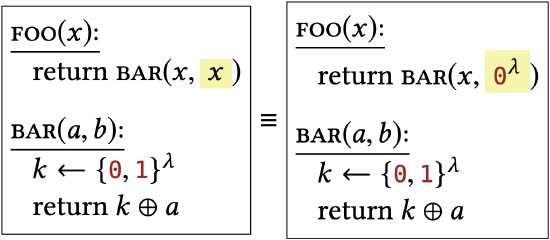 |
Their only difference is the value they assign to a variable that is never actually used. |
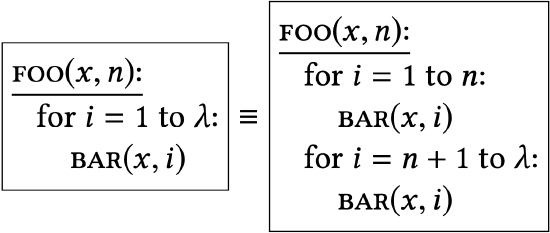 |
Their only difference is that one library unrolls a loop that occurs in the other library. |
 |
Their only difference is that one library inlines a subroutine call that occurs in the other library. |
Here are more simple examples of interchangeable libraries that involve randomness:
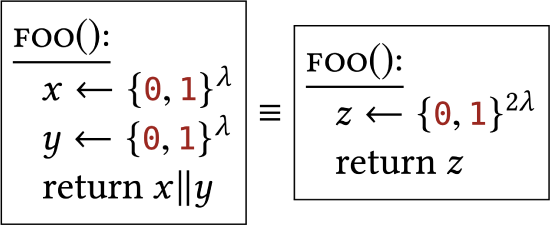 |
The uniform distribution over strings acts independently on different characters in the string ("||" refers to concatenation). |
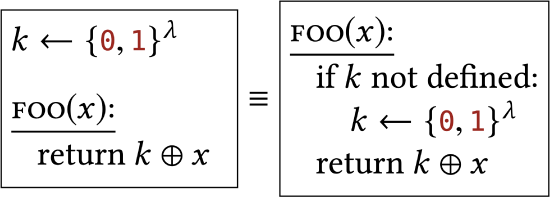 |
Sampling a value "eagerly" (as soon as possible) vs. sampling a value "lazily" (at the last possible moment before the value is needed). We assume that \(k\) is static/global across many calls to FOO, and initially undefined. |
Formal Restatements of Previous Concepts
We can now re-state our security definitions from the previous section, using this new terminology.
Our "real-vs-random" style of security definition for encryption can be expressed as follows:
An encryption scheme \(\sum\) has one-time uniform ciphertexts if:
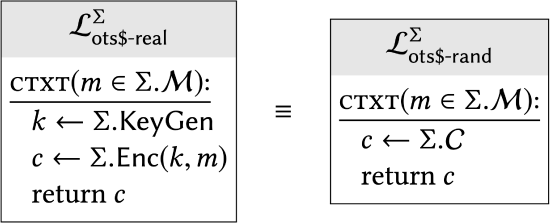
In other words, if you fill in the specifics of \(\Sigma\) (i.e., the behavior of its KeyGen and Enc) into these two library "templates", and you get two libraries that are interchangeable (i.e., have the same effect on all calling programs), we will say that \(\Sigma\) has one-time uniform ciphertexts.
Throughout this course, we will use the "$" symbol to denote randomness (as in realvs-random \()^{3}\)
Our "left-vs-right" style of security definition can be expressed as follows:
An encryption scheme \(\sum\) has one-time secrecy if:
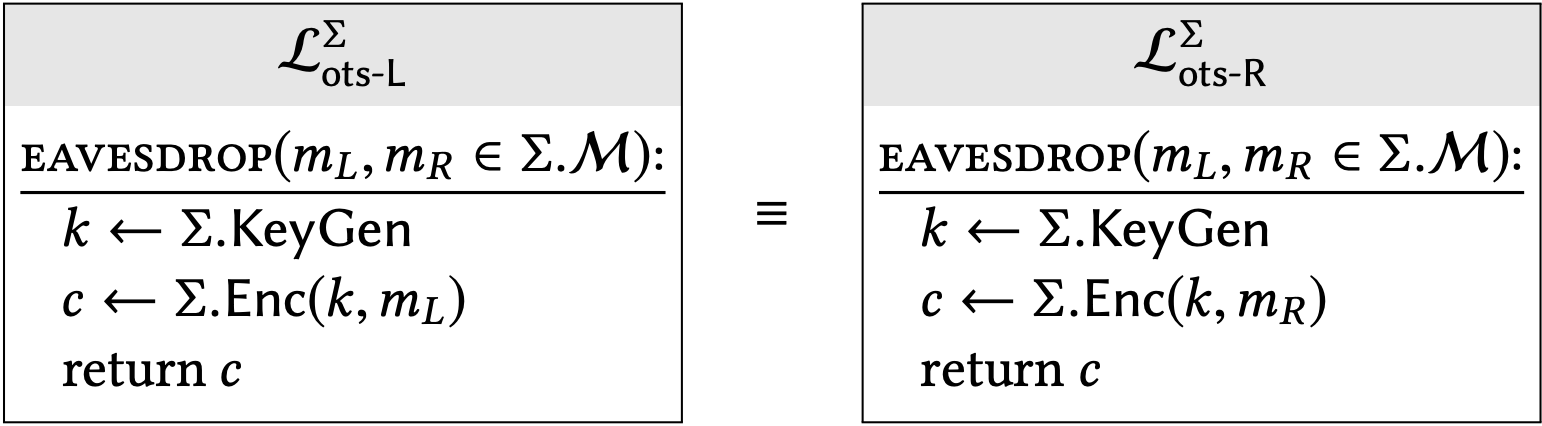
Previously in Claim \(1.3\) we argued that one-time-pad ciphertexts follow the uniform distribution. This actually shows that OTP satisfies the uniform ciphertexts definition:
One-time pad satisfies the one-time uniform ciphertexts property. In other words:

Because this property of OTP is quite useful throughout the course, I’ve given these two libraries special names (apart from \(\mathcal{L}_{\text {ots } \$ \text {-real }}^{\text {OTP }}\) and \(\mathcal{L}_{\text {ots } \$ \text {-rand }}^{\text {OTP }}\) ).
Discussion, Pitfalls
It is a common pitfall to imagine the calling program \(\mathcal{A}\) being simultaneously linked to both libraries, but this is not what the definition says. The definition of \(\mathcal{L}_{1} \equiv \mathcal{L}_{2}\) refers to two different executions: one where \(\mathcal{A}\) is linked only to \(\mathcal{L}_{1}\) for its entire lifetime, and one where \(\mathcal{A}\) is linked only to \(\mathcal{L}_{2}\) for its entire lifetime. There is never a time where some of \(\mathcal{A}\) ’s subroutine calls are answered by \(\mathcal{L}_{1}\) and others by \(\mathcal{L}_{2}\). This is an especially important distinction when \(\mathcal{A}\) makes several subroutine calls in a single execution.
Another common pitfall is confusion about the difference between the algorithms of an encryption scheme (e.g., what is shown in Construction 1.1) and the libraries used in a security definition (e.g., what is shown in Definition 2.6). The big difference is:
- The algorithms of the scheme show a regular user’s view of things. For example, the Enc algorithm takes two inputs: a key and a plaintext. Is there any way of describing an algorithm that takes two arguments other than writing something like Construction \(1.1 ?\)
- The libraries capture the attacker’s view of of a particular scenario, where the users use the cryptographic algorithms in a very specific way. For example, when we talk about security of encryption, we don’t guarantee security when Alice lets the attacker choose her encryption key! But letting the attacker choose the plaintext is fine; we can guarantee security in that scenario. That’s why Definition \(2.5\) describes a subroutine that calls Enc on a plaintext that is chosen by the calling program, but on a key \(k\) chosen by the library.
A security definition says that some task (e.g., distinguishing ciphertexts from random junk) is impossible, when the attacker is allowed certain influence over the inputs to the algorithms (e.g., full choice of plaintexts, but no influence over the key), and is allowed to see certain outputs from those algorithms (e.g., ciphertexts).
It’s wrong to summarize one-time secrecy as: "I’m not allowed to choose what to encrypt, I have to ask the attacker to choose for me." The correct interpretation is: "If I encrypt only one plaintext per key, then I am safe to encrypt things even if the attacker sees the resulting ciphertext and even if she has some influence or partial information on what I’m encrypting, because this is the situation captured in the one-time secrecy library"
Kerckhoffs’ Principle, Revisited
Kerckhoffs’ Principle says to assume that the attacker has complete knowledge of the algorithms being used. Assume that the choice of keys is the only thing unknown to the attacker. Let’s see how Kerckhoffs’ Principle is reflected in our formal security definitions.
Suppose I write down the source code of two libraries, and your goal is to write an effective distinguisher. So you study the source code of the two libraries and write the best distinguisher that exists. It would be fair to say that your distinguisher "knows" what algorithms are used in the libraries, because it was designed based on the source code of these libraries. The definition of interchangeability considers literally every calling program, so it must also consider calling programs like yours that "know" what algorithms are being used.
However, there is an important distinction to make. If you know you might be linked to a library that executes the statement " \(k \leftarrow\{0,1\}^{\lambda "}\), that doesn’t mean you know the actual value of \(k\) that was chosen at runtime. Our convention is that all variables within the library are privately scoped, and the calling program can learn about them only indirectly through subroutine outputs. In the library-distinguishing game, you are not allowed to pick a different calling program based on random choices that the library makes! After we settle on a calling program, we measure its effectiveness in terms of probabilities that take into account all possible outcomes of the random choices in the system.
In summary, the calling program "knows" what algorithms are being used (and how they are being used!) because the choice of the calling program is allowed to depend on the 2 specific libraries that we consider. The calling program "doesn’t know" things like secret keys because the choice of calling program isn’t allowed to depend on the outcome of random sampling done at runtime.
Kerckhoffs’ Principle, applied to our formal terminology:
Assume that the attacker knows every fact in the universe, except for:
- which of the two possible libraries it is linked to in any particular execution, and
- the random choices that the library will make during any particular execution (which are usually assigned to privately scoped variables within the library).
\({ }^{3}\) It is quite common in CS literature to use the "$" symbol when referring to randomness. This stems from thinking of randomized algorithms as algorithms that "toss coins." Hence, randomized algorithms need to have spare change (i.e., money) sitting around. By convention, randomness comes in US dollars.


