3.3.3: Lift and induced drag in wings
- Page ID
- 78109
In order to represent the lift curve, a dimensionless coefficient (\(C_L\)) will be used. \(C_L\) is defined as:
\[C_L = \dfrac{L}{\tfrac{1}{2} \rho_{\infty} u_{\infty}^2 S_w},\]
which can also be expressed as:
\[C_L = \dfrac{L}{\tfrac{1}{2} \rho_{\infty} u_{\infty}^2 S_w} = {1}{\tfrac{1}{2} \rho_{\infty} u_{\infty}^2 S_w} \int_{-b/2}^{b/2} \dfrac{1}{2} \rho_{\infty} u_{\infty}^2 c(y) c_l (y) dy = \dfrac{1}{S_w} \int_{-b/2}^{b/2} c(y) c_l (y) dy.\]
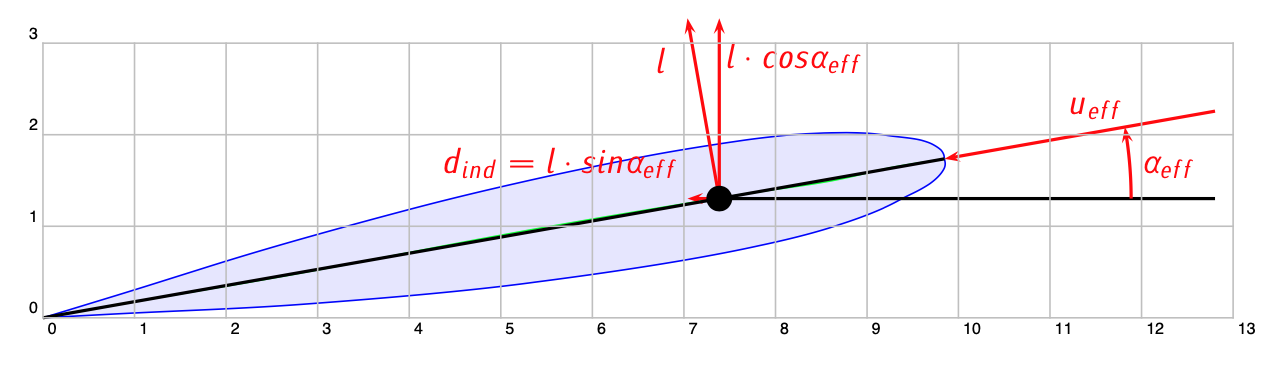
Figure 3.24: Induced drag.
Another consequence of the induced velocity is the appearance of a new component of drag (see Figure 3.24), the induced drag. This occurs because the lift is perpendicular to the effective velocity and therefore it has a component in the direction of the freestream (the direction used to measure the aerodynamic drag).


