8.3: Superposition phenomena
- Page ID
- 18083
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)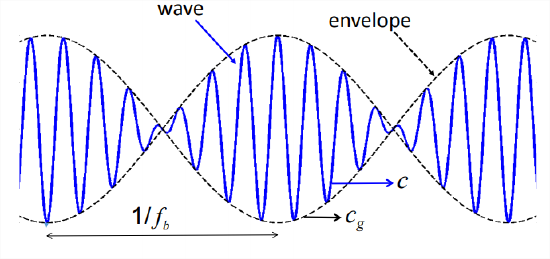
8.3.1 Beats
The “sneaker waves” that beach visitors are warned about, the spectacular spring tides (which have nothing to do with the season), and a musician’s ability to hear when two strings are exactly in tune are all examples of the phenomenon of beats (Figure \(\PageIndex{1}\)). When two oscillations with slightly different frequencies \(\omega_1\) and \(\omega_2\) occur together, what we perceive is a single oscillation with frequency equal to the average \((\omega_1 +\omega_2)/2\), modulated in amplitude by a slower frequency equal to the difference \(|\omega_1 −\omega_2|\).
Here, we will see how these results follow from the addition rule for the sine function (e.g., exercise 10f). Consider the sum of two waves having equal amplitude but different wavenumbers and frequencies:
\[\begin{align}
\frac{\eta(x, t)}{\eta_{0}} &=\frac{1}{2} \cos \left(k_{1} x-\omega_{1} t\right)+\frac{1}{2} \cos \left(k_{2} x-\omega_{2} t\right) \\
&=\cos \left(\frac{k_{1}+k_{2}}{2} x-\frac{\omega_{1}+\omega_{2}}{2} t\right) \cos \left(\frac{k_{1}-k_{2}}{2} x-\frac{\omega_{1}-\omega_{2}}{2} t\right) \\
&=\underbrace{\cos (\bar{k} x-\bar{\omega} t)}_{\text {average wave }} \underbrace{\cos \left(\frac{\Delta k}{2} x-\frac{\Delta \omega}{2} t\right)}_{\text {envelope }}\label{eqn:1}
\end{align} \nonumber \]
The first cosine function describes the “average wave”, an oscillation with wavenumber and frequency equal to the means of the individual values. The amplitude of this oscillation is modulated by a slower oscillation called the envelope, shown by the dashed curve in Figure \(\PageIndex{1}\).
Let us now assume for simplicity that we are observing the waves at a fixed location, \(x\) = 0, so the surface deflection is
\[\frac{\eta(0, t)}{\eta_{0}}=\cos (\bar{\omega} t) \cos \left(\frac{\Delta \omega}{2} t\right)=\cos (2 \pi \bar{f} t) \cos (\pi \Delta f t) \nonumber \]
(The second form employs the cyclic frequency 2\(\pi f\).) A subtlety to notice is that the oscillation has maximum amplitude when the envelope \(\cos\left( 2\pi\frac{f_1-f_2}{2}t \right)\) is equal to either +1 or -1. Beats therefore occur with double the frequency of the envelope:
\[f_{b}=2 \times\left|\left(f_{1}-f_{2}\right) / 2\right|=\left|f_{1}-f_{2}\right|; \nonumber \]
just the absolute difference between the two frequencies.
To tune a string, one begins by playing the string together with another oscillation having the correct pitch. If the string is slightly out of tune, the ear perceives beats. The tension in the string is then adjusted in whichever direction makes the beats slower. As the string approaches the correct frequency, the beat frequency approaches zero. You know the string is in tune when the beats are no longer heard.
Suppose that the waves from two ocean storms reach the beach at the same time with frequencies 10 s and 12 s. The beat frequency is then \[f_{b}=\frac{1}{10 s}-\frac{1}{12 s}=\frac{1}{60 s}. \nonumber \] There will be a big wave every 60 s, or about every 5th wave.1
8.3.2 Group velocity
In Equation \(\ref{eqn:1}\) we added two waves and found the average wave modulated by the envelope function
\[\cos \left(\frac{\Delta k}{2} x-\frac{\Delta \omega}{2} t\right), \nonumber \]
which can also be written
\[\cos \left[\frac{\Delta k}{2}\left(x-\frac{\Delta \omega}{\Delta k} t\right)\right]. \nonumber \]
The amplitude of the envelope is therefore constant in a reference frame travelling at the speed \(\Delta\omega/\Delta k\). More generally, a wave field consists of a continuous spectrum of components with different frequencies, wavenumbers and amplitudes. Wave pulses travel at the group velocity, given by \(c_g =\partial\omega/\partial k\).
In the still more general case where motion is allowed in both \(x\) and \(y\), i.e., \(\eta = \eta_0\cos\left( kx+ly-\omega t \right)\),
\[\vec{c}_{g}=\left\{\frac{\partial \omega}{\partial k}, \frac{\partial \omega}{\partial l}\right\}.\label{eqn:2} \]
1In Henri Charriere’s classic adventure novel “Papillon”, the hero escapes an island prison by hurling himself from a cliff into the ocean, having first determined that every 7th wave is large enough to carry him safely past the rocks and out to sea. The image was also used as a metaphor in the popular song “Love is the Seventh Wave”, by Sting. To the contrary, Russian sailors traditionally believe that the 9th wave is the big one (Figure \(\PageIndex{2}\), or the album “Hounds of Love” by Kate Bush). In reality, the ratio depends on the wind field and is as likely on any given day to be 5 or 10 as 7 or 9, or to not be discernible at all.


