8.1.2: Non-symmetric Binary Channel

A non-symmetric binary channel is one in which the error probabilities for inputs 0 and 1 are different, i.e., \(c_{01} \neq c_{10}\). We illustrate non-symmetric binary channels with an extreme case based on a medical test for Huntington’s Disease.

Figure 8.3: : Huntington’s Disease Test

Huntington’s Disease is a rare, progressive, hereditary brain disorder with no known cure. It was named after Dr. George Huntington (1850–1915), a Long Island physician who published a description in 1872. It is caused by a defective gene, which was identified in 1983. Perhaps the most famous person afflicted with the disease was the songwriter Woodie Guthrie.

The biological child of a person who carries the defective gene has a 50% chance of inheriting the defective gene. For the population as a whole, the probability of carrying the defective gene is much lower. According to the Huntington’s Disease Society of America, http://www.hdsa.org, “More than a quarter of a million Americans have HD or are ‘at risk’ of inheriting the disease from an affected parent.” This is about 1/1000 of the population, so for a person selected at random, with an unknown family history, it is reasonable to estimate the probability of carrying the affected gene at 1/2000.

People carrying the defective gene all eventually develop the disease unless they die of another cause first. The symptoms most often appear in middle age, in people in their 40’s or 50’s, perhaps after they have already produced a family and thereby possibly transmitted the defective gene to another generation. Although the disease is not fatal, those in advanced stages generally die from its complications. Until recently, people with a family history of the disease were faced with a life of uncertainty, not knowing whether they carried the defective gene, and not knowing how to manage their personal and professional lives.

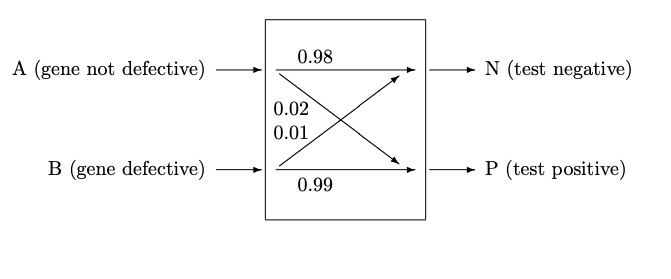
In 1993 a test was developed which can tell if you carry the defective gene. Unfortunately the test is not perfect; there is a probability of a false positive (reporting you have it when you actually do not) and of a false negative (reporting your gene is not defective when it actually is). For our purposes we will assume that the test only gives a yes/no answer, and that the probability of a false positive is 2% and the probability of a false negative is 1%. (The real test is actually better—it also estimates the severity of the defect, which is correlated with the age at which the symptoms start.)

If you take the test and learn the outcome, you would of course like to infer whether you will develop the disease eventually. The techniques developed above can help.

Let us model the test as a discrete memoryless process, with input \(A\) (no defective gene) and \(B\) (defective gene), and outputs \(P\) (positive) and \(N\) (negative). The process, shown in Figure 8.3, is not a symmetric binary channel, because the two error probabilities are not equal.

First, consider the application of this test to someone with a family history, for which \(p(A) = p(B)\) = 0.5. Then, if the test is negative, the probability, for that person, of having the defect is 1/99 = 0.0101 and the probability of not having it is 98/99 = 0.9899. On the other hand, if the test is positive, the probability, for that person, of carrying the defective gene is 99/101 = 0.9802 and the probability of not doing so is 2/101 = 0.0198. The test is very effective, in that the two outputs imply, to high probability, different inputs.

An interesting question that is raised by the existence of this test but is not addressed by our mathematical model is whether a person with a family history would elect to take the test, or whether he or she would prefer to live not knowing what the future holds in store. The development of the test was funded by a group including Guthrie’s widow and headed by a man named Milton Wexler (1908–2007), who was concerned about his daughters because his wife and her brothers all had the disease. Wexler’s daughters, whose situation inspired the development of the test, decided not to take it.

Next, consider the application of this test to someone with an unknown family history, so that \(p(A)\) = 0.9995 and \(p(B)\) = 0.0005. Then, if the test is negative, the probability of that person carrying the defective gene \(p(B \;|\; N)\) is

\[\dfrac{0.0005 \times 0.01}{0.0005 \times 0.01+0.9995 \times 0.98}=0.000005105 \tag{8.9} \]

and the probability of that person carrying the normal gene \(p(A \;|\; N)\) is

\[\dfrac{0.9995 \times 0.98}{0.0005 \times 0.01+0.9995 \times 0.98}=0.999994895 \tag{8.10} \]

On the other hand, if the test is positive, the probability of that person carrying the defective gene \(p(B \;|\; P)\) is

\[\dfrac{0.0005 \times 0.99}{0.0005 \times 0.99+0.9995 \times 0.02}= 0.02416 \tag{8.11} \]

and the probability of not having the defect \(p(A \;|\; P)\) is

\[\dfrac{0.9995 \times 0.02}{0.0005 \times 0.99+0.9995 \times 0.02}= 0.97584 \tag{8.12} \]

The test does not seem to distinguish the two possible inputs, since the overwhelming probability is that the person has a normal gene, regardless of the test results. In other words, if you get a positive test result, it is more likely to have been caused by a testing error than a defective gene. There seems to be no useful purpose served by testing people without a family history. (Of course repeated tests could be done to reduce the false positive rate.)

An information analysis shows clearly the difference between these two cases. First, recall that probabilities are subjective, or observer-dependent. The lab technician performing the test presumably does not know whether there is a family history, and so would not be able to infer anything from the results. Only someone who knows the family history could make a useful inference. Second, it is instructive to calculate the information flow in the two cases. Recall that all five information measures (\(I, L, M, N\), and \(J\)) depend on the input probabilities. A straightforward calculation of the two cases leads to the information quantities (in bits) in Table 8.1 (note how much larger \(N\) is than \(M\) if there is no known family history).

Table 8.1: Huntington’s Disease Test Process Model Characteristics

	\(p(A)\)	\(p(B)\)	\(I\)	\(L\)	\(M\)	\(N\)	\(J\)
Family history	0.5	0.5	1.00000	0.11119	0.88881	0.11112	0.99993
Unknown Family history	0.9995	0.0005	0.00620	0.00346	0.00274	0.14141	0.14416

Clearly the test conveys information about the patients’ status by reducing the uncertainty in the case where there is a family history of the disease. On the other hand, without a family history there is very little information that could possibly be conveyed because there is so little initial uncertainty.