13.2: Laplace Block Diagram with Feedback Branches
- Page ID
- 7706
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)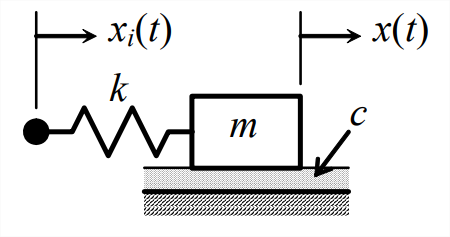Let us proceed beyond the most basic aspects of Laplace block diagrams by analyzing the \(m\)-\(c\)-\(k\) system with base excitation shown on Figure \(\PageIndex{1}\). The input is base translation \(x_i(t)\), and the output is mass translation \(x(t)\). The ODE of motion for this system (from homework Problem 9.1) is
\[m \ddot{x}+c \dot{x}+k x=k x_{i}(t)\label{eqn:13.6} \]
It is convenient to denote the input transform as \(L\left[x_{i}(t)\right]=X_{i}(s)\) and the output transform as \(L[x(t)]=X(s)\). Taking the Laplace transform of Equation \(\ref{eqn:13.6}\) with zero ICs, for the purpose of deriving the transfer function, gives
\[m s^{2} X(s)+c s X(s)+k X(s)=k X_{i}(s)\label{eqn:13.7} \]
Equation \(\ref{eqn:13.7}\) clearly leads to the transfer function,
\[T F(s) \equiv \frac{X(s)}{X_{i}(s)}=\frac{k}{m s^{2}+c s+k}\label{eqn:13.8} \]
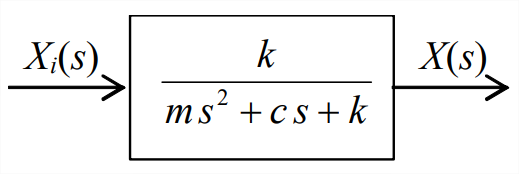
Equation \(\ref{eqn:13.8}\) is represented in the simple open-loop Laplace block diagram just above.
It will be instructive for our later study of feedback control to develop now an alternative but equivalent block diagram from Equation \(\ref{eqn:13.7}\). First, we transpose to the righthand side all terms other than the \(X(s)\) term of highest order:
\[m s^{2} X(s)=k X_{i}(s)-c s X(s)-k X(s)\label{eqn:13.9} \]
Now we “solve” algebraically for \(X(s)\) on the left-hand side of Equation \(\ref{eqn:13.9}\) simply by dividing through by the coefficient of the left-hand-side \(X(s)\):
\[X(s)=\frac{1}{s}\left\{\frac{1}{m s}\left[k X_{i}(s)-k X(s)-c s X(s)\right]\right\}\label{eqn:13.10} \]
Observe in Equation \(\ref{eqn:13.10}\) that output transform \(X(s)\) appears in the right-hand-side terms as well as on the left-hand side; these right-hand-side terms imply feedback. Using Equation \(\ref{eqn:13.10}\) leads to the following block diagram with several different transfer-function blocks and with two feedback branches:
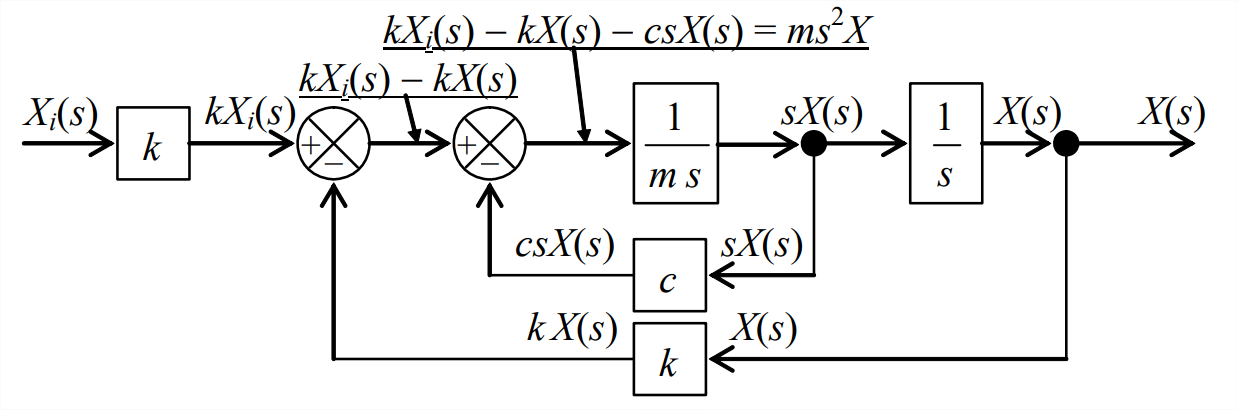
The input and output signals for every block are labeled on Figure \(\PageIndex{3}\) in order to help you relate the block diagram to Equation \(\ref{eqn:13.10}\), and you should carefully compare the equation and the diagram until you are certain that you understand.
Also, block diagram Figure \(\PageIndex{3}\) introduces two kinds of junctions. The first kind is a simple branch point (black circle), from which the same blockoutput “signal” travels onward on two different branches, as is indicated by the signal labels on Figure \(\PageIndex{3}\). The second kind is a summing junction, shown at right with input and output signals labeled. This summing junction is configured for negative feedback, so it differences the two input signals, \(\operatorname{Out}(s)=\operatorname{In}_{1}(s)-\operatorname{In}_{2}(s)\).
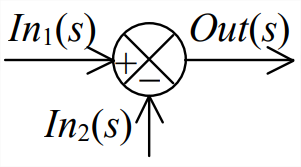
In this section, we started with ODE Equation \(\ref{eqn:13.6}\) and developed from it Laplace block diagram Figure \(\PageIndex{3}\). This approach is primarily for the purpose of presenting some important features of block diagrams. This approach is actually the reverse of the standard procedure for analysis of feedback-control systems, which we will consider in later chapters. There, we will start with the block diagram of a system, something like Figure \(\PageIndex{3}\), and derive from it the closed-loop transfer function, CLTF(s) ), which in this case is just Equation \(\ref{eqn:13.8}\). The process of deriving \(CLTF(s)\) from the system block diagram will require some new operations in block-diagram algebra; it is expedient to postpone the descriptions of these operations until we need them in later chapters.