Antiferromagnetism
- Page ID
- 328
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Magnets are of great use in everyday life from the magnets on the refrigerator to the magnetic strips on the back of credit cards. Both of these instances are examples of hard magnets, meaning they retain their magnetism easily and are therefore useful in data memory applications. Naturally magnetic materials have varying degrees of magnetism that are characterized by two things. First is the magnitude of the material’s magnetic moment, which is a vector with a certain magnitude and direction that determines the torque seen by the magnet from an applied external magnetic field. [1] The second characterization is the sign of the material’s susceptibility, χ, that describes how responsive a material is to the applied magnetic field. [4] These characterizations separate magnetic materials into the five types of magnetism; diamagnetism, paramagnetism, ferromagnetism, antiferromagnetism, and ferrimagnetism.
Ferromagnetics have been known for thousands of years and is the most common form of magnetism. These materials led to the development of the compass, electromagnets and generators without which we literally would not be where we are today [3]. Ferromagnets have a positive susceptibility and magnetic moments that align parallel with an applied external field, therefore enhancing the total magnetism and maintain that magnetism even when the applied field is removed. Above a critical temperature a ferromagnet becomes paramagnetic, where the magnetic moments still align in the general direction of the applied field but the alignment is much weaker than below the critical temperature and the material no longer retains its magnetism when the the applied field is removed [4].
Antiferromagnetic are like ferromagnets but their magnetic moments align antiparallel to the neighboring moments. This alignment occurs spontaneously below a critical temperature known as the Neel temperature. The Neel temperature is named after Louis Neel who discovered antiferromagnetics and was awarded the Nobel Prize in Physics for his work in 1970 [3]. Above the Neel temperature the material becomes paramagnetic. Antiferromagnets are less common compared to the other types of magnetic behaviors, and are mostly observed at low temperatures.
Geometry leads to magnetic properties
Antiferromagnetic materials spontaneously align their magnetic moments antiparallel when a magnetic field is applied and at temperatures below the critical temperature. The magnetization of an antiferromagnet remains constant below that critical temperature and the material retains this antiparallel alignment when the external field is removed. The magnetic moments come from the spin of the atomic valence electrons. Without a magnetic field applied to the material, the magnetic moments of each orbiting electron are all randomly oriented. When a magnetic field is applied to the material, the magnetic moments of the electrons respond and align antiparallel to each neighboring moment [4]. This is shown in Figure 1.
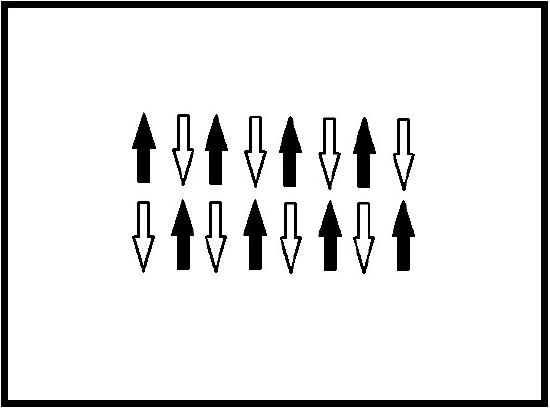
In a crystalline structure the ions in one plane have a parallel spin alignment with each other and the ions in an adjacent plane have antiparallel spin alignment, Figure 2. This creates two opposing magnetic moment sublattices and thus a total magnetic moment of zero [4].

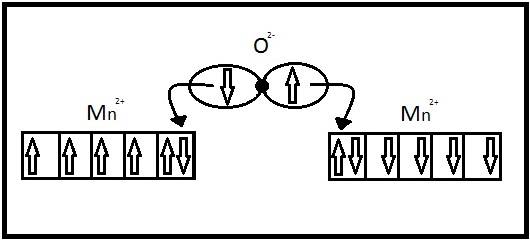
The antiparallel alignment is the result of superexchange of spin energy within the material [5]. An example of this antiferromagnetic phenomenon is Mangenese II oxide. MnO is ionic with linear chains of Mn2+ and O2- ions. The oxygen ion has a full set of valence electrons in the p orbitals directly influencing the spin of the neighboring Mn2+ ions. A schematic of the superexhange mechanism is shown in Figure 3. It is energetically favorable for this ionic compound to possess a degree of covalent bonding. Since both the Mn and O ions have full electron shells, hybridization occurs by the donation of the O2- electrons to the open orbitals of the Mn2+ ions. The Mn2+ orbitals containing up-spin electrons receives one down-spin electron from the O2- p orbital leaving one up-spin O2- electron. The O2- ion is then able to donate it’s up-spin to the next Mn2+ ion in the chain completing the bonds. This donation, however, only occurs if the next Mn2+ ion has it’s d elections in the down-spin orientation. Since by Hund’s Rule all unpaired electrons must align with parallel spins within an orbital, all of the Mn2+ electron spins must be flipped. This is the superexchange. Thus the Mn2+ ions are aligned with opposing spins within the crystalline structure [5].
Temperature Dependence
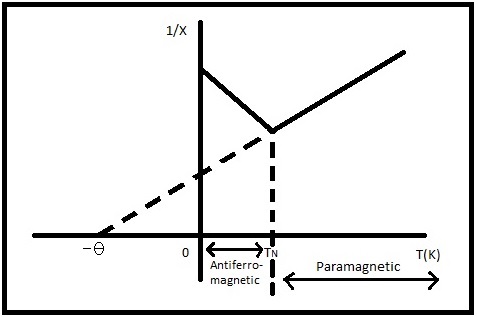
Antiferromagnetic material’s magnetic moments are temperature dependent and their critical temperature is the Neel temperature, \(T_N\), at which a magnetic phase change occurs [4]. Typically \(T_N\) is found to be below room temperature but there are some exceptions [6]. Above this temperature the material behaves paramagnetically with all magnetic moments aligned with the applied magnetic field direction therefore enhancing the overall magnetic field. Below the Neel temperature the magnetic moments spontaneously align antiparallel and the net magnetization of the material is zero because the individual magnetic moments within the sublattices cancel out [4]. The material’s susceptibility changes around the Neel temperature as well as shown in Figure 4. The susceptibility increases inversely with temperature above TN and decreases inversely below this temperature.
The temperature dependence of paramagnetic materials can be determined by the Curie Law given by
\[\chi =\dfrac{C}{T} \label{1}\]
where the susceptibility is inversely proportional to the absolute temperature, \(T\), and \(C\) is the Curie constant. The more general Curie-Weiss Law gives
\[\chi =\dfrac{C}{T-\theta} \label{2}\]
where Θ is another Curie constant in units of temperature and can be positive or negative depending on the material. [4] Therefore the material’s susceptibility is a function of temperature where an increase in temperature will decrease the material’s responsiveness to the applied magnetic field.
The increase in susceptibility for antiferromagnetic materials above TN leads to a negative Θ, see Figure \(\PageIndex{4}\), so that the Curie-Weiss Law for antiferromagnetic materials becomes [4,5]
\[\chi =\frac{C}{T+\theta} \label{3}\]
Common materials and applications
Materials
Antiferromagnets are typically ceramics of transition metals and either oxygen or sulfur [5]. The transition metal is the sublattice which has magnetic moments that respond to a magnetic field below a Neel temperature. The oxide sublattice magnetic moments respond spontaneously to the magnetization of the first lattice by aligning in the opposite direction with the same magnitude [5]. The oxygen ion alignments influence the other manganese ions and essentially tell the metal ions how to order their magnetic spins. Table 1 shows a list of some common antiferromagnetic materials and their Curie-Weiss characteristics.
| Substance | TN (K) | -Θ (K) |
|---|---|---|
| MnO | 116 | 610 |
| MnF2 | 67 | 82 |
| FeO | 198 | 570 |
| NiO | 523 | ~2000 |
| CoO | 293 |
330 |
Applications
Antiferromagnets are very interesting in nature but do not have a wide range of applications as other magnetic materials do. This is due to their lack of spontaneous magnetization [5]. However because their structural magnetization is closely related to ferrimagnets they can be used along with ferromagnets to test theoretical models used to explain ferrimagnetism [5]. The lack an overall magnetic moment which makes them suitable for providing magnetic reference points in magnetic sensors since the structure of antiferromagnets is not sensitive to external fields [3].
A growing theory and source of research on Antiferromagnets is their contribution to superconductivity. There are materials that exhibit antiferromagnetic and ferromagnetic transition states. Their corresponding structural and magnetic properties transition resemble that of a metal-insulator transition and as a result there is a large change in conductivity with an applied field. Since most nonmetallic superconductors have antiferromagnetic phase, research continues to test antiferromagnets for sought after superconducting properties [5].
Questions
- An antiferromagnetic material has an experimentally determined TN = 75 K and susceptibility of χ = 125. At 300 K the susceptibility becomes 198. What is the value of Θ for this material?
- What is the main difference between antiferromagnetism and ferromagnetism?
- An antiferromagnetic material is exposed to an external magnetic field with magnetism of M=250 mT. After 15 minutes the external field is removed. If the temperature of the material remains below the Neel temperature, what is the magnetization of the material after the external field is removed?
Answers
- -310 K
- The main difference between antiferromagnetism and ferromagnetism is the alignment of the magnetic moments. Ferromagnetic materials have magnetic moments that align parallel to the applied magnetic field whereas antiferromagnetic materials have antiparallel magnetic moments. This results in a positive magnetism for ferromagnetic materials and zero total magnetism for antiferromagnetic materials. Antiferromagnets also have a critical temperature below room temperature and a negative Cure-Weiss constant, Θ.
- The magnetization 0 T. After the material is exposed to an external magnetic field the antiparallel alignment remain if the temperature stays below TN, even with the field removed. Therefore the magnetic moments still cancel each other out and the overall magnetization is zero.
References
- B. D. Cullity, C. D. Graham (2008). Introduction to Magnetic Materials (2 ed.). Wiley-IEEE Press
- Chikazumi, Soshin. (1997). Physics of Ferromagnetism, 2nd Ed. Oxford University Press.
- Duo, Lamberto, Marco Finazzi, Franco Ciccacci. (2010). Magnetic Properties of Antiferromagnetic Oxide Materials. KGaA, Weinheim: Wiley-VCH Verlag GmbH & Co.
- Hummel, Rolf E. (2011). Electronic Properties of Materials, 4th ed. New York, NY: Springer Science+Business Media, LLC.
- Spaldin, Nicola. (2003) Magnetic Materials Fundamentals and Device Applications. Cambridge, United Kingdom: The Press Syndicate of the University of Cambridge.
Contributors and Attributions
- Katherine L. Wellmon (UC, Davis)

