11.6: Spallation (Interfacial Debonding)
- Page ID
- 7855
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Driving Force for Spallation
The presence of residual stresses in a substrate/coating system constitutes a driving force for debonding (spallation), since such stresses will almost certainly be at least partially relaxed when this occurs, releasing stored elastic strain energy. The key process is that of propagation of a crack along the interface, driven by the associated release of this stored energy. This propagation is illustrated below, for a (Stoney) case in which there is just a single (uniform) stress in the coating.
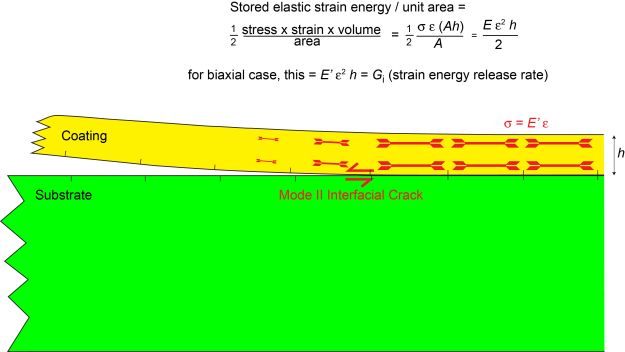
It can be seen that propagation of this interfacial crack will be energetically favoured if the driving force (strain energy release rate) is equal to or greater than the (mode II - ie shearing mode) fracture energy of the interface, Gic:
\[E_{d}^{\prime} \epsilon_{d}^{2} h\left(=\frac{\sigma_{d}^{2} h}{E_{d}^{\prime}}\right) \geq G_{\mathrm{ic}}\]
This takes no account of any barrier to initiation of the crack. In many cases, however, there are likely to be relatively large defects present in the interface, so the above condition may well lead to spallation. It certainly means that the coating is (thermodynamically) unstable. Immediate implications are (unsurprisingly) that high stresses and brittle interfaces (low Gic) make debonding more likely. Also clear (and widely observed) is that thicker coatings are more likely to debond than thinner ones.
Debonding for non-Stoney Cases
The same concept can be applied to more general cases - ie when the h<<H condition does not apply. Debonding will still tend to allow a reduction in the stored elastic strain energy, constituting a driving force for spallation. However, since there is now a distribution of stress (and strain) in the through-thickness (y) direction, an integration is needed to evaluate the driving force
\[G_{i}=\int_{-H}^{h} \frac{\sigma(y)^{2}}{E^{\prime}(y)} \mathrm{d} y\]
This is based on the assumption that these stresses become totally relaxed during debonding. This might be the case - for example, the sets of stresses and strains that have been predicted to arise from imposition of a uniform misfit strain would completely disappear if the coating could debond. In practice, however, the stress distribution within the system may be more complex than this. For example, it’s common for stresses to be created in a coating during its formation. As such a coating gets thicker, balancing of forces and moments takes place progressively, so that conditions change and the final stress distribution is not one corresponding to imposition of a uniform misfit strain. In such cases, debonding may leave some residual stresses (and residual curvature of the coating and possibly of the substrate). The net driving force may then be written
\[G_{i}=\int_{-H}^{h} \frac{\sigma(y)^{2}}{E^{\prime}(y)} \mathrm{d} y-\int_{-H}^{h} \frac{\sigma_{r}(y)^{2}}{E^{\prime}(y)} \mathrm{d} y\]
where σr(y) is the residual stress distribution after debonding.
Debonding of coatings is, of course, commonly observed, since virtually all coatings contain at least some stresses and the associated strain energy can rise above the critical level - for example, as a result of temperature changes, thickening (eg oxide growth), stiffening (eg due to sintering), applied forces or bending moments etc. Also, the toughness (fracture energy) of the interface (Gic) may fall with time - eg due to chemical attack etc. The video clips below give some examples of how coating spallation can be observed and analysed.
https://www.doitpoms.ac.uk/tlplib/co...os/debond1.mp4
Spontaneous Debonding. This video shows a set of coated samples (zirconia on alumina substrates) being withdrawn from a furnace and cooled by gas jets. The cooling creates differential thermal contraction stresses and, once these have become sufficiently large, coatings can spontaneously debond. Such an event can be seen at the end of this short video.
https://www.doitpoms.ac.uk/tlplib/co...eos/kappa1.mp4
In Situ Curvature Measurement. This video, which has a commentary, explains how, provided the substrate is relatively thin, the deposition of a coating (in this case by thermal spraying of ceramics onto metal substrates) generates curvature, which can be monitored as the coating thickness increases. In conjunction with a numerical model, this can be used to infer the residual stress levels in coatings produced under a range of conditions.
https://www.doitpoms.ac.uk/tlplib/co...eos/kappa2.mp4
Debonding during Cooling of Thin Substrate with Coatings. This video, which has a commentary, explains how stored residual stresses provide a driving force for debonding (spallation). It is also explained how estimates can be made of the interfacial toughness (fracture energy) from observations of debonding during cooling.
https://www.doitpoms.ac.uk/tlplib/co...eos/kappa3.mp4
Debonding under Applied Load of Coatings with Residual Stresses. This video, which has a commentary, goes briefly through the 4-point bend delamination test for coatings that already contain stored residual stresses. It is shown how this can be used to measure the interfacial fracture energy.


