24.2: The Theory of Electromigration
- Page ID
- 32716
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Electromigration is the transport of material in a conductor under the influence of an applied electric field. All conductors are susceptible to electromigration, therefore it is important to consider the effects the electrical current resulting from the applied field may have on the conductor.
The net force exerted on a single metal ion in a conductor has two opposing contributions: a direct force and wind force.
![]()
Direct Force
Application of an electric field results in an electrostatic pull being exerted on the metal ion core. The direction and magnitude of the electrostatic pull depend on the charge on the ion core, modified by screening effects. Positively charged ion cores (cations) are pulled towards the cathode, whilst negatively charged ion cores (anions) are pulled towards the anode. The direct force, Fd, is given by:
\[F_{\mathrm{d}}=a Z e E=a Z e j p\]
where a = factor accounting for screening (a<<1); Z = actual valence of the atom; e = electron charge (1.6 x 10-19 C); j = current density (A m-2); ρ = resistivity (Ω m).
When electromigration in conductors was discovered, it was thought that the migration effects would be analogous to those in liquid electrolysis.
Consider for example, the electrolysis of the molten salt, NaCl. The Na+ ions move towards the cathode, whilst the Cl– ions move towards the anode (as shown in the diagram below), as the electric field is applied.
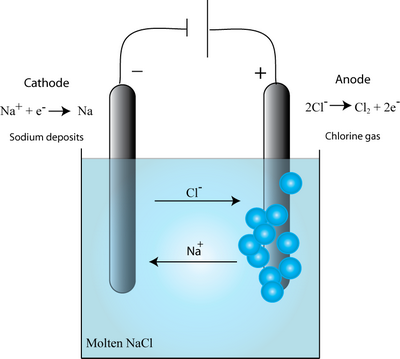
It was thought that the metal ions within a wire would always move towards the cathode as in electrolysis. While this is found in some cases, in the metallization of interest for ICs (which are based on good metal conductors) the migration was observed to be in the opposite direction – towards the anode. This startling effect results from the wind force.
Wind Force
Electrons move along the metallization line, carrying the current. These electrons tend to scatter. Electron scattering takes place at imperfections within the lattice: vacancies, impurities, grain boundaries, dislocations and even phonon vibrations of the metal ions from their ideal positions! The scattering of electrons gives us electrical resistance but it also results in a force exerted on the metal ion core.
An electron changes direction as a result of a scattering event. This change in direction is accompanied by an acceleration, which results in a force. The electrons are also accelerated within the electric field. When the overall electron drift velocity is established, the force on the ions due to electron scattering is in the direction of the electron flow – this is known as the wind force, Fw, which can be described as:
\[F_{\mathrm{w}}=-\mathrm{en}_{\mathrm{e}} \lambda \sigma_{t} E\]
where ne = density of electrons;σi = cross-section for collision; λ = mean free path.

The term electron wind comes from an analogy with, for example, a tree being blown in the wind. The wind is analogous to the electron current, the leaves on the tree to the metal ions in a conductor.
Net Force
In good conductors, such as the ones used in IC metallization, the electron wind force is the dominant force felt by the ion cores, resulting in atomic migration towards the anode. The net force on the ions can be represented as:
\[F_{n e t}=F_{\text {wind }}+F_{\text {direct }}=\left(Z_{w}+Z_{d}\right) ejp =Z^{*}ejp\]
where Zwind, Zdirect and Z* respectively refer to the effective valences for the wind force, direct force and the net force.
Diffusion
The migration of the metal ion cores occurs by diffusive jumps. In the cases of interest in metallization, this is self-diffusion or substitutional diffusion by the vacancy mechanism.
To find out more about diffusion, refer to Diffusion in the MATTER Software.
The rate of diffusion is described by the diffusion coefficient (or diffusivity) with units of m2 s–1. The diffusivity, D, has an Arrhenius dependence on temperature according to:
\[D=D_{0} \exp (-Q / R T)\]
where D0 = constant (m2 s–1); Q = activation energy for diffusion (J mol–1); R = gas constant (8.314 J mol–1 K–1); T = absolute temperature (K).
The diffusion coefficient and the activation energy are dependent on the nature of the material.
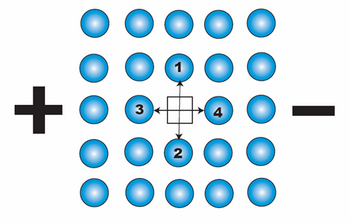
We depict above a 2-D section through a simple cubic metallic lattice showing a single vacant site. The vacancy can jump into either position 1, 2, 3 or 4 (i.e. it can exchange position with the atom in position 1, 2, 3 or 4). Without any external influence, the probability of the vacancy jumping into each site is equal, as its energy on every site is the same and the activation energy for a jump from site to site is always the same.
When an electric field is applied, the activation energies for a jump into sites 1 and 2 remain identical, whereas the activation energy for a jump into site 4 is smaller than that into site 3. This results in a biasing of vacancy diffusion jumps towards the cathode. This net flux of vacancies towards the cathode corresponds to the net flux of atoms (or ions) towards the anode. This flux of metal ions can be considered to be due to the effective charge, Z*, on the ion and the associated net force as described above.
\[J=C D F_{n e t} / R T=C D Z^{*} e \rho j / R T\]
where J = atomic flux (atoms m2 s–1) ; C = atomic concentration (atoms m–3); D = diffusivity (m2 s–1).
Note that this overall net flux is exceedingly minute. There is only a very slight biasing of atomic movement e.g. in 1000 atoms 499 would diffuse towards the anode whilst 501 diffuse towards the cathode, resulting in a net of 2 atoms migrating towards the cathode. Electromigration is a very slow process, taking time.


