31.6: Electrolyte

This section of the TLP describes the fundamental properties of the most common materials used as electrolytes in SOFCs.

There are several criteria that the electrolyte has to meet. It must be:

• Dense and leak tight
• Stable in reducing and oxidising environments
• A good ionic conductor at operating temperatures
• Non-electron conductor
• Thin to reduce ionic resistance
• Extended in area for maximum current capacity
• Thermal shock resistant
• Economically processable

The materials used, are solid, ion-conducting ceramics. There are two main groups of such ion conductors: fluorite structured and perovskite structured, besides new materials such as hexagonal structured oxides. The three most common electrolyte materials are: doped ceria (CeO₂), doped lanthanum gallate (LaGaO₃) (both are oxygen ion conductors) and doped barium zirconate (BaZrO₃) (a proton conductor). The concentration and type (ionic radius) of the dopants influence the material properties strongly. Dopants, that cause the least strain and hence the least influence on the potential energy landscape of the parent lattice, have the biggest effect on the conductivity.

In an oxide ion conductor, current flows by the movement of oxide ions through the crystal lattice. This is a thermally activated process, where the ions hop from one lattice site to the other (from one potential valley to the other) in a random way. When an electric field is applied, there is a drift in one direction superimposed on the random thermal motion.

Potential energy in an electric field in a periodic crystal

Ionic conduction depends on the mobility of the ions and therefore on temperature. At high temperatures, the conductivity can reach 1 S cm^-1, which is of the same order of magnitude as for liquid electrolytes. The crystal has to contain unoccupied sites that are equivalent to the occupied sites by lattice oxygen ions. The energy barrier for migration from an occupied site to an unoccupied site must be small (≤1 eV). This might seem unusual since the relative size of the oxygen ions is big and it seems more likely that the smaller metal ions migrate in an electric field. That is why there are only a few special structures that make oxygen ion migration possible: fluorite structured oxides, perovskites, LAMOX family and BIMEVOXes.

Fluorite oxides are the most common and classical oxygen ion conducting materials. The crystal structure consists of a cubic oxygen lattice with alternate body centres occupied by eight coordinated cations. The cations are arranged into a face centred cubic structure with the anions occupying the tetrahedral sites. This leaves a rather open structure with large octahedral interstitial void.

https://www.doitpoms.ac.uk/tlplib/fu...s/Zirconia.mp4

Rotating zirconia lattice

The general formula has the form AO₂, where A is usually a big tetravalent cation, e.g. U, Th, Ce. Since Zr⁴⁺ is too small to sustain the fluorite structure at low temperatures, it has to be partly substituted with a larger cation, called dopant. Doping involves usually substituting lower valence cations into the lattice. In order to maintain charge neutrality oxygen vacancies have to be introduced, which allow oxygen ion migration.

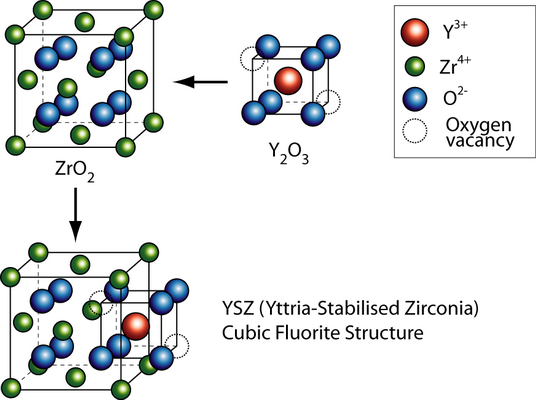
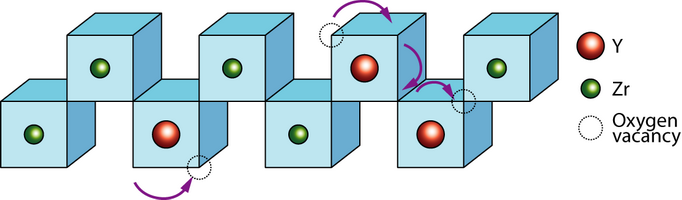
Vacancy transport in YSZ

An interesting feature of the fluorite structure is that it can sustain a high degree of substitution. A very disordered and open structured material results from this, which promotes ionic conduction.

High resolution transmission electron micrograph depicting the nickel and YSZ interface (Image courtesy of Technical University of Tokyo)

By substituting the host cation sites with either rare earth or an alkaline earth element, just as with yttria-stabilised zirconia (YSZ), an increase of ionic conduction can be achieved. Zirconia (zirconium dioxide, ZrO₂) in its pure form has a high melting temperature and a low thermal conductivity. The applications of pure zirconia are restricted because it shows polymorphism. It is monoclinic at room temperature and changes to the denser tetragonal phase from circa 1000 °C. This involves a large change in the volume and causes extensive cracking. Hence zirconia has a low thermal shock resistivity. The addition of some oxides results in stabilising the cubic phase and the creation of one oxygen vacancy, i.e. \(2[Y'_{Zr}] = [V_{O^-}] \)

\[ Y_2O_3(ZrO_2) \leftarrow 2Y'_{Zr} + 3O^x_o + V_o \]

Phase diagram of partially stabilized zirconia (PSZ)

Partially stabilized zirconia (PSZ) is a mixture of zirconia polymorphs: a cubic and a metastable tetragonal ZrO₂ phase is obtained, since an insufficient amount of stabilizer has been added. PSZ is also called tetragonal zirconia polycrystal: TZP. PSZ is a transformation-toughened material since the induced microcracks and stress fields absorb energy. PSZ is used for crucibles because it has a low thermal conductivity and a high melting temperature. The addition of 16 mol% CaO or 16 mol% MgO or 8 mol% Y₂O₃ (8YSZ) is enough to form fully stabilized zirconia. The structure becomes cubic solid solution, which has no phase transformation when heating from room temperature up to 2500 °C. Because of its high oxide ion conductivity, YSZ is often used for oxygen sensoring and solid oxide fuel cells.

Scanning electron micrograph showing 8 mol% Y₂O₃ (8YSZ) surface (Image courtesy of Altair Nanotechnologies, Inc)

It might be expected that an increase of the dopant concentration would lead to an increase of conductivity. This correlation only applies to low dopant concentrations because at higher levels, the first and second electron coordination shells dopants start interacting with the oxygen vacancies and the conductivity decreases. The conductivity can be calculated as follows:

\[ \sigma = \frac{A}{T}[V_{O^-}][\bar{V_{O^-}}]exp(\frac{-E}{RT}) \]

where E is the activation energy for conduction, T is the temperature, R and A are constants \( [\bar{V_{O^-}}] \) is an unoccupied oxygen vacancy.

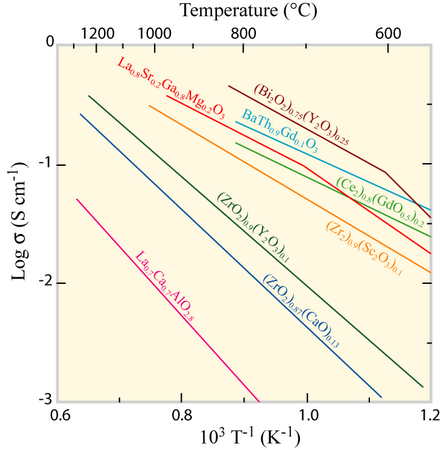
Conductivity as a function of temperature, data taken from Ref.[3].

In present fuel cells, the electrolyte of choice is zirconia, stabilised by either 3 mol% Y₂O₃ (3YSZ) or 8 mol% Y₂O₃ (8YSZ). YSZ is not the best ion conductor, but it is the cheapest to process and has low enough electronic conductivity. There are many other materials that conduct oxides but the advantages of YSZ: abundance, chemical stability, non-toxicity and economics make it the most suitable material at present. Drawbacks are high thermal expansion coefficient and hence problems with sealing the fuel cell. The world demand for YSZ is rising, but luckily, Zr is one of the most common elements of the Earth’s crust usually in the form of silicate zircon (ZrSiO₄). This material has to be purified since SiO₂ tends to block the ionic and electron paths.

Yttria is the main stabilizer used and about 13-16 wt% have to be added to give a fully stabilized cubic material. More rare dopants’ supply such as scandia could present a problem in the future.

Another interesting fluorite structured material is CeO₂ doped with 10 mol% GdO (GCO). It is especially useful for lower temperature applications. But GCO is an electron conductor in the reducing environment at the anode and hence short-circuiting is a problem.

Fabrication of zirconia electrolyte films is usually done by tape casting or vapour deposition.

The second highly interesting group of solid state ion conductors is perovskites. The general perovskite stoichiometry is ABO₃.

https://www.doitpoms.ac.uk/tlplib/fu...Perovskite.mp4

Rotating perovskite lattice

Due to the number of combinations (2+4, 5+1, 3+3) to have the total charge of +6 on AB, the high stability of the structure and the wide variety of cations that can be accommodated within, perovskites have a wide range of properties, which are suitable not only for SOFCs but also as ferroelectrics, oxidation catalysts or superconductors. High ionic conductivity in perovskites is achieved by doping the material with trivalent elements, such as Y on the Zr site of BaZrO₃ for example, so that oxygen vacancies are introduced. The conductivity of ABO₃ perovskites strongly depends on the size of the A and less so on the size of the B cation, since the oxides have to migrate through a triangular space, consisting of two large A cations and one smaller B cation. The enlargement of this triangular space facilitates the migration of oxide ions through the lattice. Hence we can expect higher ion conductivity with larger lattice dimensions.

In order to incorporate hydroxyl groups into onto the vacant oxide sites, the material is exposed to humid atmospheres. The second proton of the water molecule attaches to some other oxygen atom in the structure. Due to the loose bonding between the hydrogen ion and the oxygen atom, conduction occurs easily, by hydrogen ions jumping from one oxygen to the other.

The perovskites LaGaO₃ and BaZrO₃ proved to be highly interesting since their structure is very tolerant and can accommodate large concentrations of dopants but less than in YSZ (hence the ion conductivity of perovskites is always less than that of YSZ).

A particular composition: La_0.9Sr_0.1Ga_0.8Mg_0.2O_3-d (LSGM) has been found to have similar, purely ionic conductivities to CeO₂, also at low temperatures (<600 °C). The evaporation of Ga causes problems with stability though. Other problems, such as LSGM reactivity with Nickel electrodes have been solved by adding a CeO₂ buffer layer between the two materials.

In case of an electrolyte-supported design, the electrolyte has to be 120–150 mm thick. Operation at low temperatures requires a thin electrolyte since the conductivity is proportional to temperature. For operation temperatures between 600–800 °C, the electrolyte layer thickness cannot exceed 20 mm to ensure high enough conductivity.

Electrolyte fabrication process

The latest production method involves electrochemical vapour deposition used to make tubular cells (at Westinghouse). Doped lanthanum manganite (cathode material) is placed in a low-pressure chamber and zirconium chloride plus yttrium chloride vapour is passed along the outside of the tube, as water vapour is passed on the inside of the tube. A more conventional production method is tape casting:

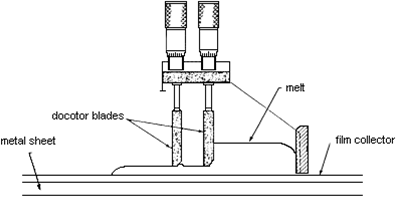
Tape casting