32.5: Demostrations
- Page ID
- 33016
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Bouncy Balls
A bouncy ball is made of a polymer that is above its Tg at room temperature, with cross-linking keeping the ball in its spherical shape. The height that the ball rebounds to when dropped is dependent on how much energy is lost during the bounce. At room temperature the ball loses little energy when it deforms, so can rebound to a large fraction of its original height. As the temperature is reduced, the viscosity of the polymer increases, so more of the elastic strain energy is dissipated, and the ball does not bounce as high.
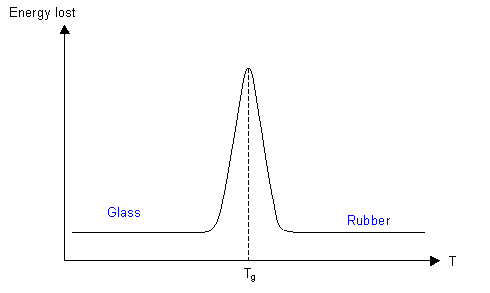
At Tg nearly all the energy is dissipated, and the ball barely bounces at all. As the temperature is reduced more to below Tg, there is not enough energy for conformational changes to occur, and the ball becomes glassy. The energy losses above Tg are due to the viscosity as the conformation changes and the polymer chains move past each other, and since these movements do not occur, the energy is not dissipated, so the ball bounces again.
The videos show how high a bouncy ball bounces at different temperatures. The videos were filmed at 500 frames a second, and played back at 50 frames a second, so are at one tenth of actual speed.
|
https://www.doitpoms.ac.uk/tlplib/gl...videos/25c.mp4 Ball bouncing at 25°C, well above Tg |
https://www.doitpoms.ac.uk/tlplib/gl...ideos/-50c.mp4 Ball bouncing at -50°C, just above Tg |
|
https://www.doitpoms.ac.uk/tlplib/gl...ideos/-70c.mp4 Ball bouncing at -70°C, close to Tg |
https://www.doitpoms.ac.uk/tlplib/gl...deos/-190c.mp4 Ball bouncing at -190°C, well below Tg |
The second set of videos are close ups of the bounce itself, showing the deformation of the ball. The ball bounces both above and below Tg, although the process is very different. Above Tg the conformation of the polymer chains changes, and the deformation of the ball can clearly be seen. Below Tg, the conformation is frozen, so it is only the interatomic bonds that are strained, and the macroscopic deformation is much less, and is not observable in the videos. bouncing
|
https://www.doitpoms.ac.uk/tlplib/gl...ber-bounce.mp4 Rubbery bounce, well above Tg |
https://www.doitpoms.ac.uk/tlplib/gl.../tg-bounce.mp4 Bounce near Tg |
|
https://www.doitpoms.ac.uk/tlplib/gl...ass-bounce.mp4 Glassy bounce, well below Tg |
|
Silly Putty
The time dependence on the deformation of a material that exhibits a glass transition can be demonstrated with "Silly Putty". If a ball of putty is left at rest at room temperature, then it will slowly deform plastically under its own weight. However, if the ball of putty is hit with a hammer, again at room temperature, then it is possible to smash the putty into pieces.
|
https://www.doitpoms.ac.uk/tlplib/gl...utty-small.mp4 Silly putty deforming under its own weight |
https://www.doitpoms.ac.uk/tlplib/gl...tty-bounce.mp4 Silly putty striking the ground |
|
https://www.doitpoms.ac.uk/tlplib/gl...utty-smash.mp4 Silly putty being hit by a hammer |
|
The first video shows a small ball of putty (initially approximately 40 mm diameter) deform under its own weight at room temperature. The deformation took just over 40 minutes, so the film has been speeded-up 80 times. The height of the ball can be judged against the background. The initial deformation is much more rapid than towards the end, as the following numbers show:
| Loss of height / mm | Time / mins:secs |
|---|---|
| 5 | 1:10 |
| 10 | 5:30 |
| 15 | 25:00 |
| 16 | 42:00 |
The other two videos were both filmed at 1000 frames per second, and played back at 4 frames per second, so are at 1/250th of real speed.
The second video is of a ball of putty hitting the ground after being dropped from a height of 1 m. The ball deforms, but returns to its original shape as it rebounds. When a ball of putty is dropped it rebounds to a large fraction of its original height.
The third video is of a ball of putty being hit with a hammer, also at room temperature. The theory states that at fast strain rates the material will be glassy, and this is shown in this video, although it may not seem like it at first. The ball deforms quite a lot initially, and then breaks apart. This can be explained by the putty being glassy, with an elastic modulus low enough for there to be a visible strain before a critical strain is reached and brittle fracture occurs.


