33.8: Liquefaction

The phenomenon of soil liquefaction describes failure of saturated or partially saturated soil that, upon application of an applied stress, behaves as a liquid when it fails. In the real world these failures usually result from earthquakes leading to landslides.

It was proposed by Casagrande that grain rotation can result in a change from an interlocking grain structure to a flowing grain structure. He tested this hypothesis by applying an impact force to a tank filled with loose sand. The aggregate remained solid until the instant the force was applied. The application of the force caused a high transient pore pressure to be generated within the aggregate, reducing the effective stress to near zero, so that liquefaction flow occurred.

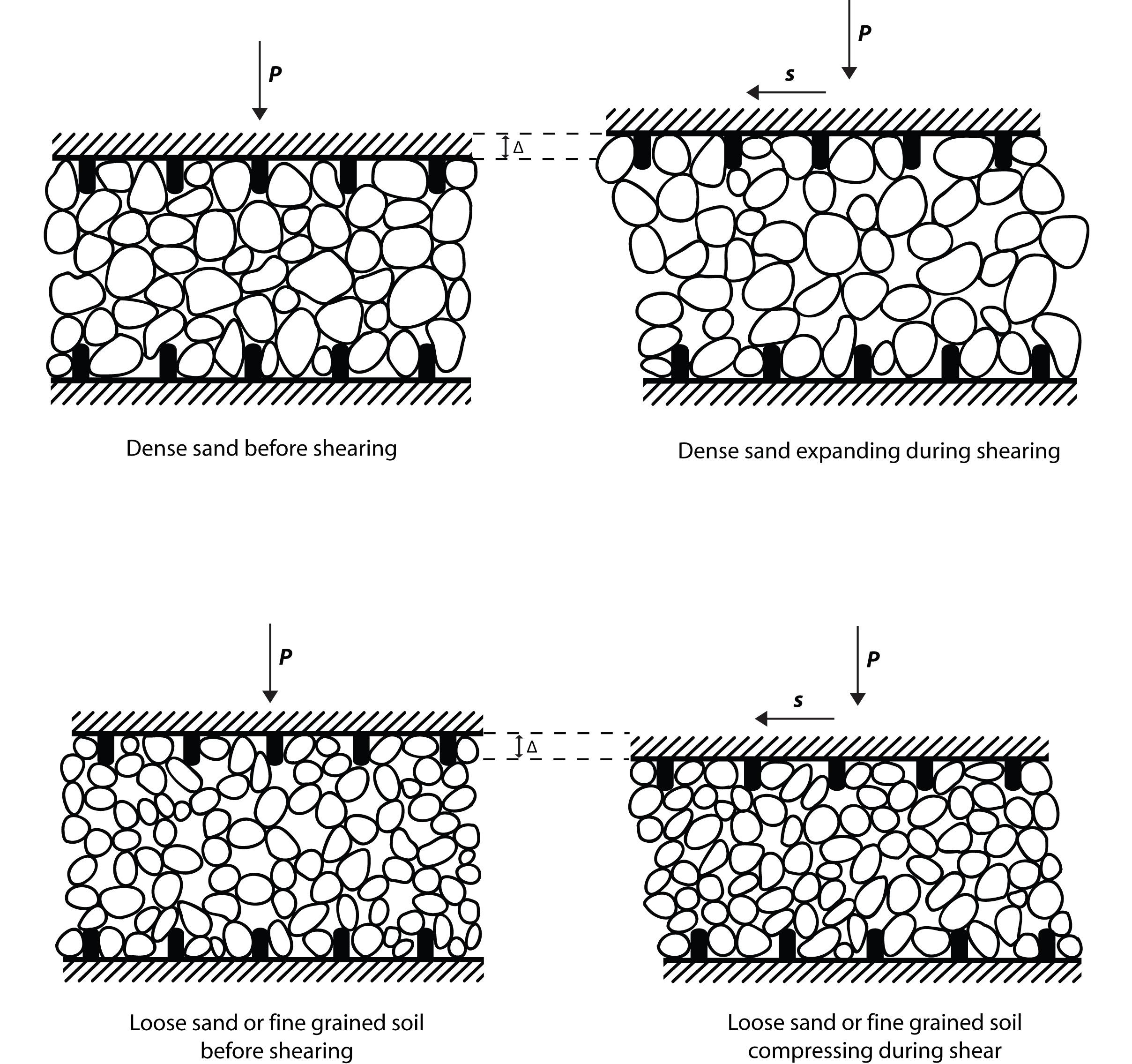
A large body of soil is not safe from liquefaction unless it is compacted below the critical void value. This is due to the pore pressure changes during shear. Casagrande studied this using triaxial compression tests. He showed how with shear at a constant normal stress the peak strength (starred point) of dense sand increased as it expands. Loose sand showed a fall in porosity and dense sand showed an increase. After the displacement both loose and dense sand have reached a peak porosity n₀ where the sand flows under constant shear stress.

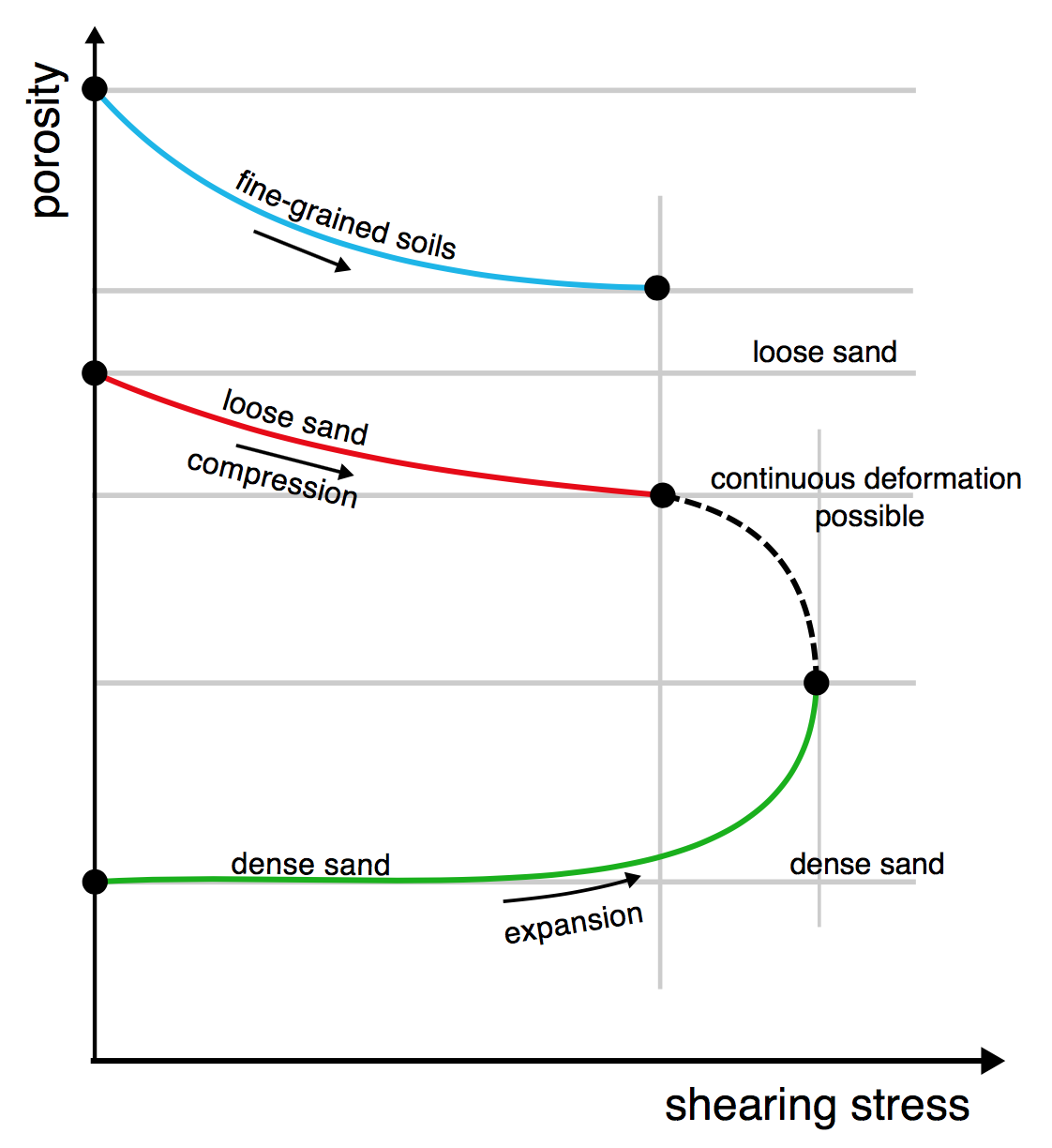
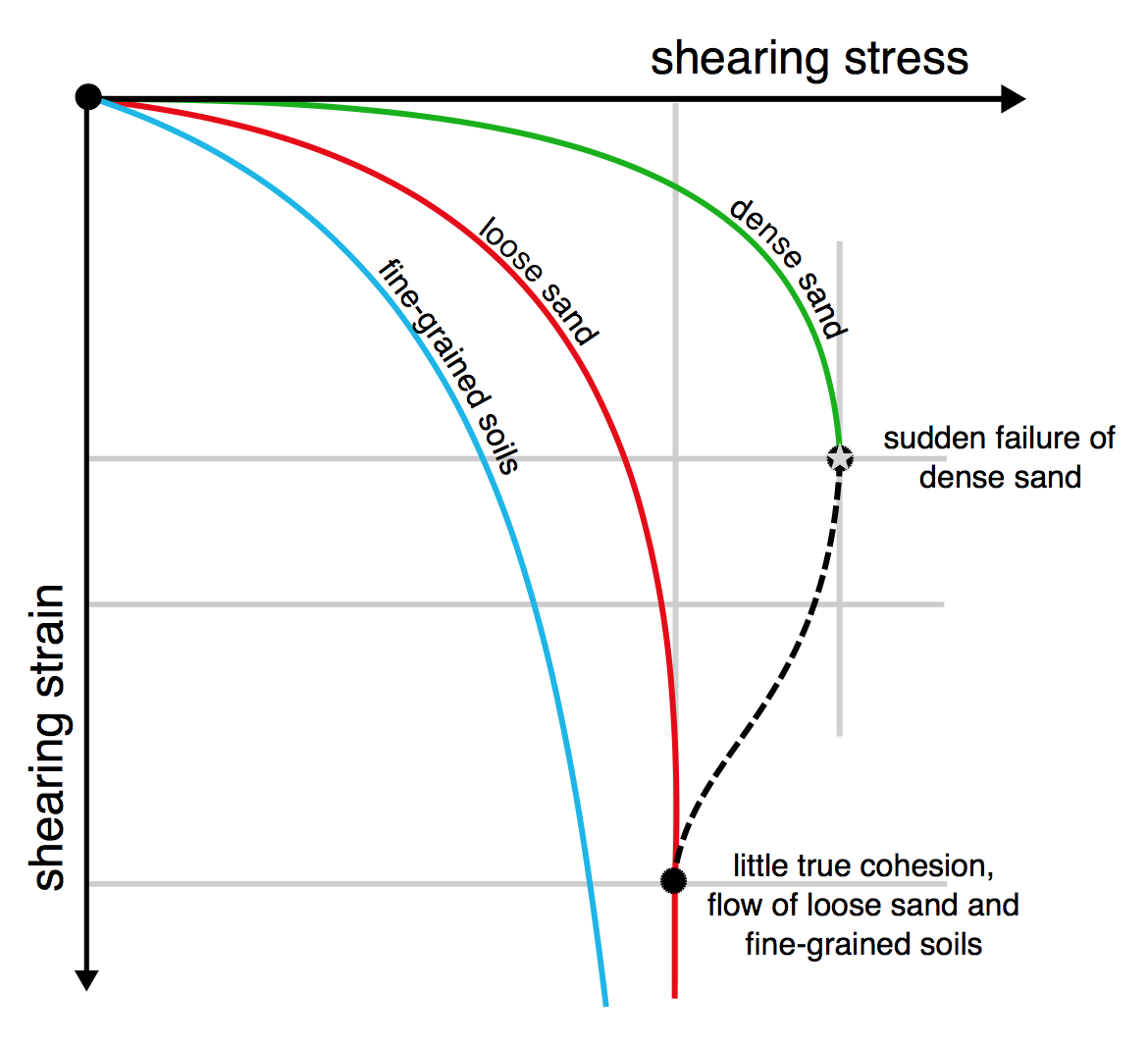
This critical porosity n₀ is independent of the effective pressure. If silty sand is compacted below n₀, it will not be at risk of liquefaction. Compression with drained shear is the most effective way of reducing the risk of liquefaction of an existing sample as the water content is also reduced.

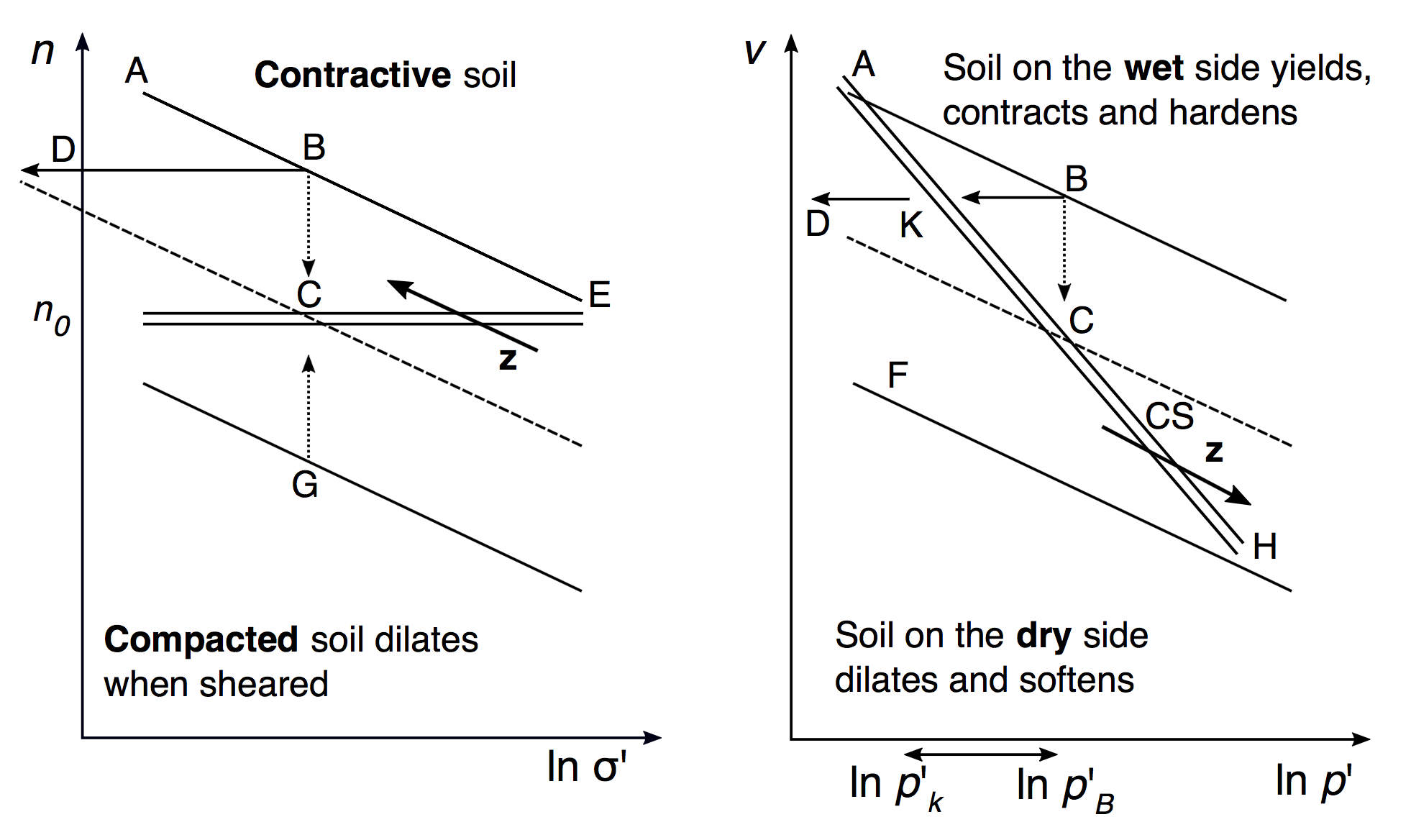
In the left-hand graph above, the dashed line BC represents a drained test and the solid line BD an undrained test. The double horizontal line in the left-hand graph is the critical void ratio n₀. In the graph on the right, the double line at an angle to both the horizontal and the vertical is a λ-line representing soil at critical state, CS, as a function of the specific volume of aggregate, v, and the logarithm of the effective compressive stress p' applied to the aggregate relative to a standard compressive stress state of 1 kPa.

For the critical void ratio theory, compression with large deformation depends on the initial state, while in CS theory an aggregate of grains does not retain any record of its initial structure. The states predicted under Casagrande’s model differ from those predicted by the line AH in CS theory. Under CS theory the dashed line still follows the same path BC but the solid line instead stops short at BK and does not continue from K to D. In 1975 Casagrande revised his theory of constant critical porosity to adopt the CS line which combines specific volume v and effective pressure p’. The slope of the double λ-line in CS is greater than the slope of the elastic κ compression lines, shown in the right-hand graph as lines parallel to FH.

The bold arrows marked z show the main differences between the two initial theories. In the Casagrande model, the vector z shows that the reduction of pressure is unsafe as it results in a swelling of the aggregate. This moves from a safe dilative state to an unsafe contractive state. There is a likelihood of liquefaction in the contractive state. In the CS theory, the vector z shows that increasing the effective pressure moves the aggregate from a safe dilative state to an unsafe contractive state. This means that even very dense sand can liquefy if the effective pressure is high enough; this is especially relevant for aggregates with a high water content.

Concerns of liquefaction in the real world

As well as natural disasters there are other situations where liquefaction needs to be taken into account. Liquefaction in bulk cargo carriers has a catastrophic impact on ship stability that can result in large losses of life. Nickel ore is one of the most dangerous granular materials to transport due to the fine grain size and moisture content that sits in the pores. There are many precautions and safety checks before a cargo is approved to leave port. Before the cargo experiences compaction at sea it appears in a solid dry state due to frictional forces between grains.

During transport, the motions of a ship on the waves cause compaction of the cargo so that the pore size between the grains is reduced. Since the grains themselves can be very fine, there can be limited permeability, and so very little water drainage can occur. Once the pore water has been compressed, the pressure will start to push the grains apart, causing the grains no longer to be in contact, so the surface friction is lost. The shear strength of the cargo is reduced to zero and so it flows out to a level surface when liquefaction has occurred. Fortunately, this is often a transient phenomenon because the cargo can settle back into a more dense state.

Some nickel ores have a clay-like consistency. In these materials liquefaction is instead a fatigue process where after a certain number of stress cycles the material will fail as the cohesion of the material collapses. This can result in the entire cargo becoming liquid simultaneously. As the cargo does not often fill the entire hold, there is sufficient space for the liquefied material to flow and destabilise the ship. Once this has occurred, it is very difficult to regain stability and it can result in the capsize of a ship in a matter of minutes.