20.7: Questions

Quick questions

You should be able to answer these questions without too much difficulty after studying this TLP. If not, then you should go through it again!

What does a point in reciprocal space correspond to in real space?

a	A lattice point
b	A plane
c	A lattice vector
d	A unit cell

Answer

B

Open-ended questions

The following questions are not provided with answers, but intended to provide food for thought and points for further discussion with other students and teachers.

Use this Ewald Sphere to find the angle at which a (2 0 0) plane will satisfy the Bragg condition for this lattice and wavelength. (Assume that it is a primitive lattice):

Deeper questions

The following questions require some thought and reaching the answer may require you to think beyond the contents of this TLP.

What is the reciprocal lattice of a reciprocal lattice?

Answer

The original real lattice.

From the Fourier analysis we know that G.R = n where R is the real lattice vector and G is the reciprocal lattice vector. Now H.G = n where H is the reciprocal reciprocal lattice vector when finding the new reciprocal lattice. Hence the reciprocal reciprocal lattice is the real lattice.

What is the reciprocal Bravais lattice of an FCC lattice?

Hint: First find the primitive FCC unit cell, and it's real vectors.

Answer

The primitive form of the FCC lattice has lattice vectors

\[a=\frac{a}{2}\left[\begin{array}{lll}
1 & 1 & 0
\end{array}\right], b=\frac{a}{2}\left[\begin{array}{lll}
1 & 0 & 1
\end{array}\right], \quad c=\frac{a}{2}\left[\begin{array}{lll}
0 & 1 & 1
\end{array}\right]\]

These give reciprocal lattice vectors:

\[a^{*}=\frac{1}{a}\left[\begin{array}{lll}
1 & 1 & \overline{1}
\end{array}\right], b^{*}=\frac{1}{a}\left[\begin{array}{lll}
1 & \overline{1} & 1
\end{array}\right], \quad c^{*}=\frac{1}{a}\left[\begin{array}{lll}
1 & 1 & 1
\end{array}\right]\]

The 3 reciprocal primitive lattice vectors are arranged tetragonally, giving a primitive (rhombohedral) BCC unit cell. They can be summed to find the conventional unit cell:

\[a^{*}+b^{*}=\frac{2}{a}\left[\begin{array}{lll}
1 & 0 & 0
\end{array}\right], \quad a^{*}+c^{*}=\frac{2}{a}\left[\begin{array}{lll}
0 & 1 & 0
\end{array}\right], b^{*}+c^{*}=\frac{2}{a}\left[\begin{array}{lll}
0 & 0 & 1
\end{array}\right]\]

What are the reciprocal lattice vectors of a lattice with

\[\mid a=\left(\begin{array}{l}
1 \\
0 \\
0
\end{array}\right), b=\left(\begin{array}{c}
1 / 2 \\
\sqrt{3} / 2 \\
0
\end{array}\right) \text { and } c=\left(\begin{array}{l}
0 \\
0 \\
2
\end{array}\right)\]

Answer

\[a^{*}=\frac{\left(\begin{array}{c}
1 / 2 \\
\sqrt{3} \\
6 \\
0
\end{array}\right) \times\left(\begin{array}{l}
0 \\
0 \\
2
\end{array}\right)}{\left(\begin{array}{l}
1 \\
0 \\
0
\end{array}\right) \cdot\left(\begin{array}{c}
1 / 2 \\
\sqrt{3} / 2 \\
0
\end{array}\right) \times\left(\begin{array}{l}
0 \\
0 \\
2
\end{array}\right)}=\left(\begin{array}{c}
1 \\
-1 / \sqrt{3} \\
0
\end{array}\right)\]

\[b^{*}=\frac{\left(\begin{array}{l}
0 \\
0 \\
2
\end{array}\right) \times\left(\begin{array}{l}
1 \\
0 \\
0
\end{array}\right)}{\left(\begin{array}{l}
1 \\
0 \\
0
\end{array}\right) \cdot\left(\begin{array}{c}
1 / 2 \\
\sqrt{3} / 2 \\
0
\end{array}\right) \times\left(\begin{array}{l}
0 \\
0 \\
2
\end{array}\right)}=\left(\begin{array}{c}
0 \\
2 / \sqrt{3} \\
0
\end{array}\right)\]

\[c^{*}=\frac{\left(\begin{array}{l}
1 \\
0 \\
0
\end{array}\right) \times\left(\begin{array}{l}
1 / 2 \\
\sqrt{3} / 2 \\
0
\end{array}\right)}{\left(\begin{array}{l}
1 \\
0 \\
0
\end{array}\right) \cdot\left(\begin{array}{c}
1 / 2 \\
\sqrt{3} / 2 \\
0
\end{array}\right) \times\left(\begin{array}{l}
0 \\
0 \\
2
\end{array}\right)}=\left(\begin{array}{c}
0 \\
1 / 2 \\
0
\end{array}\right)\]

On the (105) maps below what are the in- and out-of-plane reciprocal space coordinates for the films? Try to convert them into real space cell parameters. (As shown previously c is out-of-plane and both films have hexagonal unit cells).

AlxGa(1-x)N	InxGa(1-x)N

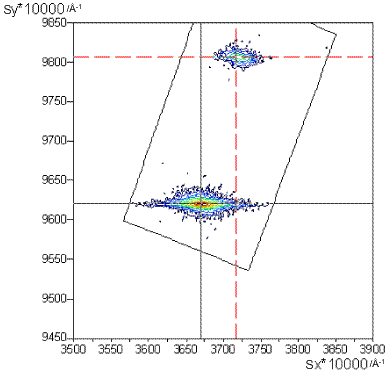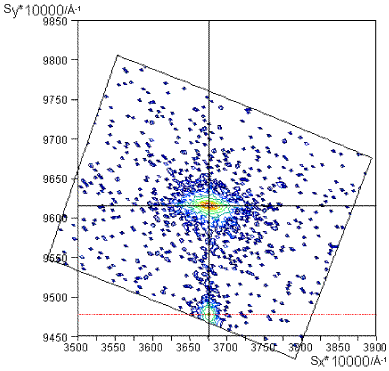Answer

The film peaks are weaker than the GaN substrate peaks.
The Al_xGa_(1-x)N has an out-of-plane parameter of 0.981 Å^-1 and an in-plane one of 0.372 Å^-1.
Therefore,

\[c = \frac{5}{0.981} = 5.10 \AA\]

and

\[a = \frac{1}{0.372 \times \cos{30}} =3.1\]

The In_xGa_(1-x)N has an out-of-plane parameter of 0.948 Å^-1 and an in-plane one of 0.3675 Å^-1.
Therefore,

\[c = \frac{5}{0.948} = 5.27 \AA\]

and

\[a = \frac{1}{0.3675 \times \cos{30}} =3.14\]

Note Al_xGa_(1-x)N real cell smaller than In_xGa_(1-x)N one as expected.