21.9: Questions

Quick questions

You should be able to answer these questions without too much difficulty after studying this TLP. If not, then you should go through it again!

Ferrous scrap metal is easily separated from non-ferrous, using an electromagnet. However, non-ferrous metals still need to be separated before recycling. What materials properties allow the separation of non-ferrous metals in the eddy current separator?

a	Mass and Density
b	Conductivity and Mass
c	Conductivity and Density
d	Conductivity

Answer

C

In the eddy current separator a rotating magnet block causes a changing magnetic flux. The metal is moving through the changing flux and swirling currents are formed as a result. What effect do these swirling currents have?

Hint: Think about Lenz's law

Answer

The swirling currents will form magnetic fields that act to oppose the changing magnetic field that induced the currents. These magnetic fields interact with the magnetic field from the rotating magnet block and cause the non-ferrous metal to be ejected from the stream of scrap along the conveyor with more energy than materials with lower conductivities.

Tin is separated from steel cans using principles involving corrosion. What method is used to decide the conditions of corrosion such that the steel will not dissolve into solution as well?

Answer

Pourbaix diagrams plots of pH vs. electrode potential that show the behaviour of materials under different conditions. The pourbaix diagrams of tin and iron are compared to find conditions such that iron will be passivated and tin will be corroded.

How is the tin removed from the solution?

a	Precipitation and filtering
b	Electrolysis
c	The tin is not removed from the solution
d	Fractional distillation

Answer

B

What property of copper could be exploited in order to separate it from steel and other plastics before recycling?

a	Copper is more ductile than the other materials named
b	Copper has a lower melting temperature than the other materials named
c	Copper has a lower ductile-brittle transition than the other materials named
d	Copper is shinier than the other metals named

Answer

C

Deeper questions

The following questions require some thought and reaching the answer may require you to think beyond the contents of this TLP.

If the calorific value of coal is 30.9 MJ kg^-1 and it is combusted at 40% efficiency in a power station, how many kilograms of coal would be needed to produce 1 kg of primary production aluminium and 1 kg of recycled aluminium respectively?

Hence, or otherwise, find a percentage value for the energy saved by recycling aluminium.

Hint: Think about the energy involved

Answer

First, work out the actual energy gained by combusting coal at 40% efficiency:
30.9 × 0.4 = 12.36 MJ kg^-1

Therefore we can work out the ratio of Al:Coal, since the units are the same (MJ kg^-1):
260 ÷ 12.36 = 21
So, for every kg of primary aluminium produced, 21 kg of coal need to be burned:

6 ÷ 12.36 = 0.485
10 ÷ 12.26 = 0.815
So, for every kg of recycled aluminium, 0.485 < kg < 0.815 of coal is needed.

We can rewrite this as a percentage:
(0.815 ÷ 21) × 100 = 3.88 ≈ 4%
100 - 4 = 96%

Since some energy is used in the transport and sorting of aluminium before it is recycled, the nominal percentage usually quoted for the energy saved by recycling aluminium is 95%.

Today, an increasing amount of metal is being galvanised. In automotives and home appliances the advantage of Galvanised Steel is that even if the Zn layer is scratched, the steel will not rust. This comes from the fact that Zn is much more reactive with O₂ than Steel (Fe) and so reacts with the oxygen preferentially. However, in 5 or 6 years when these galvanised items reach the end of their lives, a huge amount of zinc-plated scrap will need to be recycled.

Zn has a boiling point of 907°C.  This is a lower temperature than the melting point of steel in the EAF, so if Zn is present in the melt, it boils off and is separated.  This forms a vapour. Carbon dioxide gas is also present in these exhaust fumes, and since Zn is highly reactive with oxygen, it displaces the carbon to form ZnO particles. These are in the form of an extremely fine dust that is a problem for workers at EAF plants. It can be collected, although it has to be further refined to become useful Zn (expending more energy).

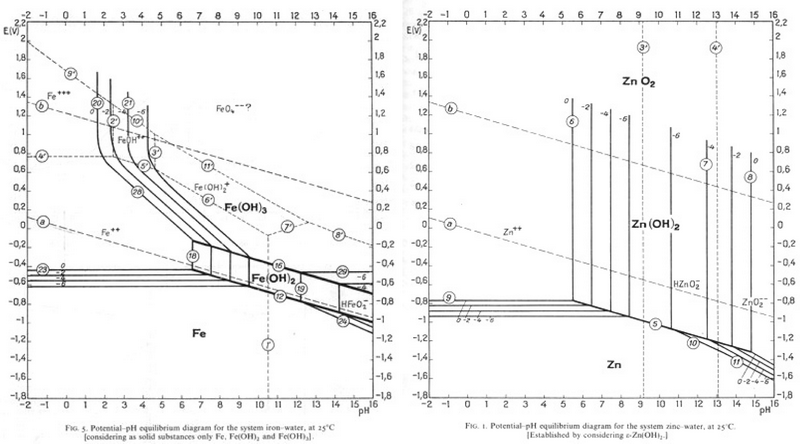
Since Zn is most commonly electroplated to steel, it could be removed in the same way as tin is removed from steel, and this process is currently being researched.  Find a pH and an E° value that would allow Zn to be corroded and Fe to be passivated?

Answer

In the TLP, the equations used to form the pourbaix diagrams are shown in calculation. In reality, conclusions can be drawn by comparing the two pourbaix diagrams, as shown. The electrochemical equations are only needed to design the actual experimental procedure for separating the metals.

In the image, the pourbaix diagrams for Iron and Zinc are superimposed, with the passivation region for iron in green and the corrosion region for zinc in red. The regions covered by both green and red are the regions of pH and E° that would be suitable for the desired reaction to occur.

An exemplar energy calculation for the primary formation of Al is shown in the TLP. Magnesium is another metal that has to be extracted via electrolysis rather than direct reduction with carbon, since it is more ‘reactive’ than carbon.

MgCl₂(l) → Mg(l) + Cl₂(g)

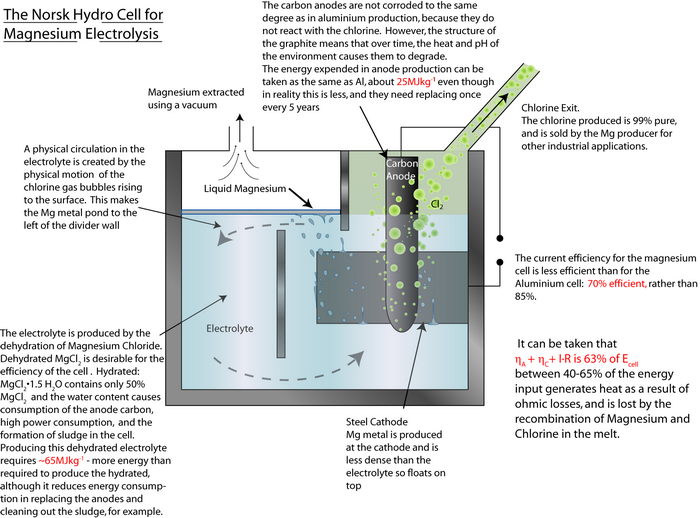
By using the same method as that used in the TLP for aluminium, calculate the energy required to produce 1 kg of magnesium.

Answer

====

\[\Delta G^{o}=-z F E^{o}\]

\[E^{o}=-\frac{\Delta G^{o}}{2 F}=-\frac{(-500000)}{2 \cdot 96485}=2.59\]

\[E_{cell}=\left|E_{r e v}\right|+\eta_{A}+\eta_{C}+I \cdot R\]

\(E_{cell}\) can be taken to be equak to \(E^o\) since \(\frac{RT}{6F}\ln a_{MgCl_2} = 0\)

(The activity of pure MgCl₂ = 1, hence )

Therefore

\[E_{\text {cell}}=2.59 \cdot\left(\frac{100}{37}\right)=7 \mathrm{~V}\]

\[Q=\frac{2 F}{\frac{M_{Mg}}{1 \mathrm{~kg} \cdot 10^{3} \mathrm{gkg}^{-1}}}=\frac{2 \cdot 96540}{\frac{24}{10^{3}}}=8 \times 10^{6} \mathrm{C}\]

However, the current efficiency for magnesium is ~70%, so the actual value is

\[Q^{\prime}=\left(8 \times 10^{6}\right) \cdot \frac{1}{0.7}=11.43 \times 10^{6}\]

\[Q \cdot E_{cell}=11.43 \times 10^{6} \cdot 7=80 \mathrm{MJ} \mathrm{kg}^{-1}\]

Again, this electrical energy is produced using fossil fuels that are only 30-40% efficient

\[\left(80 \times 10^{6}\right) \cdot \frac{1}{0.35}=229 \mathrm{MJ} \mathrm{kg}^{-1}\]

Adding this to the other energy-intensive parts of the production (from the information on the diagram)

Energy required in producing the electrodes:  ≈ 25 MJ kg^-1
Energy required in producing the electrolyte: ≈ 65 MJ kg^-1

Total energy for the cell = (230 MJ kg^-1 + ~25 MJ kg^-1 + ~ 65 MJ kg^-1) ≈ 320 MJ kg^-1

Therefore, the total energy ≈ 320 MJ kg^-1

This is a huge amount of energy, almost double that for producing aluminium. For this reason, recycling magnesium products is crucial.

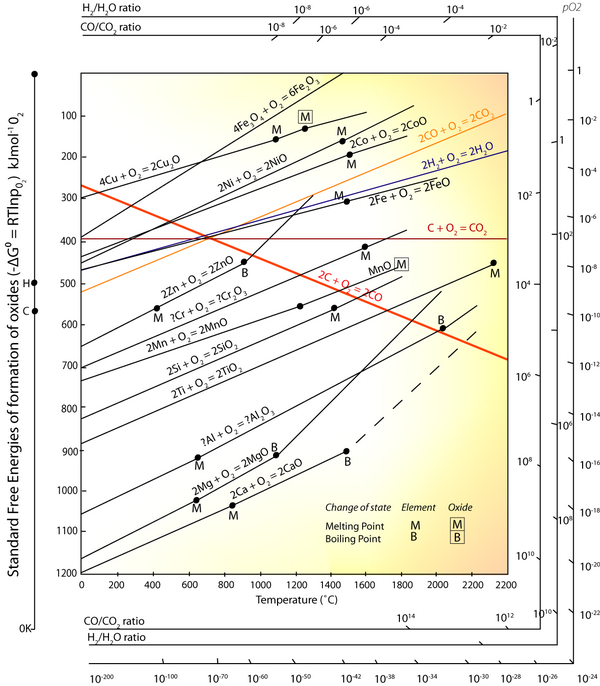
In the electric arc furnace, conditions are created such that impurities resulting from poorly sorted steel scrap are reduced/oxidised into slag. It was explained in the TLP how the Ellingham diagram can be used to predict which metals will come out of solution with the steel and which ones will not. Phosphorus (P), Copper and Tin cannot come out of solution this way, and other methods have to be employed (as described) to remove them from solution.

It was explained that P is removed from the EAF by addition of CaO to produce a very basic slag.

Why does this occur?

Phosphorus can oxidise to P₂O₅ as shown:

\[\frac{4}{5} P+O_{2} \rightarrow \frac{2}{5} P_{2} O_{5}\]

The driving force for P oxidation is lower than that for the oxidation of Fe. Thermodynamically, as depicted in the Ellingham diagram, oxidation of P from Fe melt is not favourable. As the concentration of P in the melt is low, the activity of P in the Fe melt is in the order of magnitude of 10^-3, further decreasing the driving force for oxidising and thus removing P from the melt.

It will be possible to remove P from the Fe melt by an oxidation reaction, provided the driving force is greatly increased by achieving a very low activity for P₂O₅ in the slag in equilibrium with Fe such that P₂O₅ is transferred from the melt to the slag. For this to happen in the slag, the ΔG value for the oxidation of Fe to FeO needs to equal the ΔG value for P to P₂O₅.

If we assume that Fe is pure (which is not unreasonable) and the slag is saturated with FeO, ΔG of the reaction:

\[\Delta G \cong \Delta G^{0}+R T \ln \frac{a_{Fe0}}{a_{Fe}}\]

becomes equal to ΔG°, because the activity term .

*Note that in practice an oxidising slag actually contains 20 mol% FeO (at which the activity of FeO is ~0.2).

For P to be oxidised into the slag spontaneously, the reaction

\[\Delta G \cong \Delta G^{0}+R T \ln \frac{\left(a_{P_{2} O_{5}}\right)^{\frac{2}{5}}}{\left(a_{P}\right)^{\frac{4}{5}}}\]

needs to be at least equal the value of ΔG° from the iron reaction.

Since the value of ΔG° for the oxidation of P is known – it can be found from the Ellingham diagram at the temperature within the EAF, one can calculate the required activity of the P₂O₅ to allow it to move into the slag in the EAF. Find this value.

Hints: Assuming a_P ~ 10^-3
T = Temperature in the EAF : 1600°C
R = molar gas constant 8.31 J mol^-1 K^-1
Find ΔG° for the reactions from the Ellingham diagram:

Answer

ΔG° for P 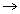 P₂O₅ = – 240 kJ mol^-1
ΔG° for Fe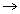  FeO = – 298 kJ mol^-1

\[\Delta G^{0}(F e) \cong \Delta G^{0}(P)+R T \ln \frac{\left(a_{P_{2} O_{5}}\right)^{\frac{2}{3}}}{\left(a_{P}\right)^{\frac{4}{5}}}\]

\[\Delta G^{0}(F e) \cong \Delta G^{0}(P)+\left(\left(\frac{2}{5} \cdot R \cdot T \ln a_{P_2O_5}\right)-\left(\frac{4}{5} R \cdot T \ln a_{P}\right)\right)\]

\[\frac{\Delta G^{0}(F e)-\Delta G^{0}(P)+\left(\frac{4}{5} R \cdot T \ln a_{P}\right)}{\frac{2}{5} \cdot R \cdot T} \cong \ln a_{P_{2} O_{5}}\]

\[e^{\frac{\Delta G^{0}(F e)-\Delta G^{0}(P)+\left(\frac{4}{5} R T \ln a_{P}\right)}{\frac{2}{3} \cdot R T}}\cong a_{P_{2} O_{5}} \cong 9.01 \times 10^{-11}\]

Thus the activity of P₂O₅ in the slag at the operating temperature (~1873 K) should be as low as ~10^-10 for achieving preferential oxidation of P from a Fe melt. In a very basic slag (containing ~50 mol% CaO), the activity of P₂O₅ at 1873K is very low at ~10–20, thus providing a large driving force for de-phosphorisation. This arises due to the high thermodynamic stability of calcium phosphates allowing P to be locked into the slag phase.

When the same calculation is done for copper, it is found that currently, no compound exists that can reduce the activity of copper in the melt to the value required to provide a driving force for its oxidation out of the slag. If an economically feasible compound exists, it would ensure the stability of the steel recycling industry for years to come.