3.5: Inconsistencies in the Elementary Beam Theory
- Page ID
- 21487
The equations presented in Section 2.6 under the ADVANCED TOPIC were derived without any approximate assumption. In order for the beam to be in equilibrium, shear force \(V\) must be present, when the beam is under pure bending (uniform bending over the length of the beam). It is the shear stress \(\sigma_{xz}\) that give rise to the shear force, according to the definition, Equations (2.4.8-2.4.10). Therefore any inconsistencies must come from the strain-displacement relations as well as constitutive equations, where some approximations were introduced.
The presence of the shear stresses \(\sigma_{xz} = \sigma_{13}\) means that shear strains \(\epsilon_{13} = \epsilon_{xz}\) must develop according to Equation (4.16).
\[\epsilon_{xz}(z) = \frac{\sigma_{xz}(z)}{2G} \label{4.32}\]
The shear strain is defined as
\[\epsilon_{xz} = \frac{1}{2} \left( \frac{\partial u_x}{\partial z} + \frac{\partial u_z}{\partial x}\right)\]
The Euler-Bernoulli assumption tells us that the shear strain vanishes. Then, Equation \ref{4.32} is violated because the LH is zero while the RH is not. Suppose for a while that \(\epsilon_{xz} = 0\). Then
\[\frac{\partial u_x}{\partial z}= -\frac{\partial w(x)}{\partial x} = -\theta (x) \label{4.34}\]
where \(u_z = w(x)\) is independent of the coordinate \(z\). Integrating Equation \ref{4.34} one gets
\[u_x(z) = u^{\circ} − z \theta\]
which is equivalent to the plane-remain-plane and normal-remain-normal hypothesis, introduced in Chapter 1. Assume now that the out-of-plane strain is a certain given function of \(z\). Performing the integration of Equation \ref{4.32} in a similar way as before, one gets
\[u_x(z) = u^{\circ} − z \theta + \int \epsilon_{xz}(z) dz \label{4.36}\]
It transpires from the above results that deformed section are not flat but are warped instead. The amount of warping is given by the third term in Equation \ref{4.36}.
Can we estimate the amount of warping? Yes, but we have to go ahead of the presented material and quota the solution for the deflected slope \(\theta\) of the beam. Le’s settle on the simplest case of a clamped cantilever beam loaded at its tip by the point force \(P\)
\[\theta = \frac{Pl^2}{2EI}\]
This solution will be derived in Chapter 4.
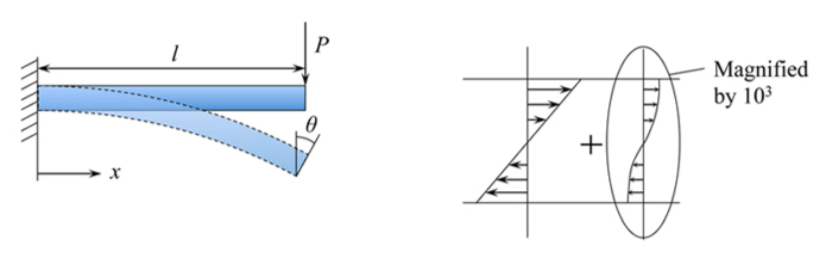
Another result needed is the distribution of shear stresses across the height of the beam. For the rectangular section beam \((b \times h)\), the shear stress is a parabolic function of \(z\)
\[\sigma_{xz}(z) = \frac{3}{2} \frac{P}{A} \left[1 − \frac{z^2}{(h/2)^2} \right] \]
The corresponding strain is calculated from Equation \ref{4.32}. Assume that there is no axial force, \(N = 0\), so from Equation (3.4.3) \(\epsilon^{\circ} = 0\) and \(u^{\circ} = 0\). After integration, the displacement profile defined by Equation \ref{4.36} becomes
\[u_{x}(z) = -\frac{Pl^2}{2EI}z + \frac{1}{2\epsilon} \frac{3}{2} \frac{P}{A} \left[z − \frac{z^3}{3(h/2)^2} \right] \]
In order to quantify the correction of the displacement field due to warping, let’s calculate the maximum values of the two terms at \(z = − \frac{h}{2}\). The first term arising from the EulerBernoulli assumption gives
\[u^{\mathrm{I}}_{x} (z = − \frac{h}{2}) = \frac{\rho l^2}{2EI} \frac{h}{2}\]
The second correction term is
\[u^{\mathrm{II}}_{x} (z = − \frac{h}{2}) = \frac{1}{2G} \frac{P}{A} \frac{h}{2}\]
The ratio of the two terms is
\[\left|\frac{u^{\mathrm{II}}_{x}}{u^{\mathrm{I}}_{x}} \right| = \frac{E}{2G} \frac{I}{Al^2} = \frac{E}{2G} (\frac{\rho}{l})^2 \label{4.42}\]
where \(\rho\) is the radius of giration of the cross-section. For a rectangular cross-section \((b \times h)\),
\[\rho^2 = \frac{I}{A} = \frac{bh^3}{12bh} = \frac{h^2}{12}\]
The ratio \(E/2G\) is
\[\frac{E}{2G} = \frac{E}{2\frac{E}{2(1 + \nu)}} = (1 + \nu)\]
Then, the relative amplitude of warping from Equation \ref{4.42} is
\[\left|\frac{u^{\mathrm{II}}_{x}}{u^{\mathrm{I}}_{x}} \right| = \frac{ (1 + \nu)}{12} \left(\frac{h}{l}\right)^2\]
For a typical beam with \(\frac{l}{h} = 20\), the above ratio becomes \(0.25 \times 10^{−3}\)!!! In order to compare the plane and wrapped cross-section, the amount of warping had to be magnified thousand times, see Figure (\(\PageIndex{1}\)). It can be concluded that the effect of warping is of an order of \(0.1 %\) and can be safely neglected in the engineering beam theory. In other words the “rein” of the Euler-Bernoulli assumption is unchallenged.
Another inconsistency of the elementary beam theory is that the uniaxial stress gives rise to the tri-axial strain state. In particular, from the 3-D constitutive equation, the strain components
\[\epsilon_{yy} = \epsilon_{zz} = − \frac{\nu}{E}\sigma_{xx}\]
Let’s take as an example the same cantilever beam with a tip load. The bending moment at root of the beam is \(M = Pl\), and from the stress formula,
\[\sigma_{xx} = \frac{Pl}{I} z\]
From the definition \(\epsilon_{yy} = \frac{du_y}{dy}\), and after integrating with respect to \(y\), one gets
\[u_y = − \frac{Pl\nu}{IE} zy\]
The maximum displacement occurs at \(z = \frac{h}{2}\) and \(y = \frac{b}{2}\). Making use of the beam deflection formula (see Chapter 4)
\[\delta = \frac{Pl^3}{3EI} \text{ or } \frac{Pl}{EI} = \frac{3\delta}{l^2} \label{4.49}\]
the formula for the maximum displacement of a beam, normalized with respect to the beam thickness becomes
\[\frac{(u_y)_{max}}{h} = \frac{3}{4} \nu \left( \frac{\delta}{h}\right) \left( \frac{h}{l}\right)^2 \label{4.50}\]
What is the range of the normalized beam deflections \(\delta\)? The beam deflects elastically until the most stressed fibers reach yield of the materials, \(\left. \sigma_{xx} \right|_{z= \frac{h}{2}} = \sigma_y\).
Then, from the stress formula
\[\sigma_{y} = \frac{Pl}{I} \frac{h}{2}\]
Combining the above expression with the beam deflection formula, Equation \ref{4.49}, the estimate for the maximum elastic tip displacement
\[\frac{\delta}{h} = \frac{2}{3} \frac{\sigma_y}{E} \left( \frac{l}{h}\right)^2 \label{4.52}\]
Combining Equations \ref{4.50} and \ref{4.52}, the expression for the maximum normalized displacement of the corner of the cross-section becomes
\[\frac{(u_y)_{max}}{h} = \frac{\nu}{2} \frac{\delta_y}{E}\]
With realistic values \(\nu = \frac{1}{3}\) and \(\frac{\sigma_y}{E} = 10^{−3}\), the amount of maximum change of the width of the beam is \(0.1 %\) of the beam height. Such a tiny change in the cross-sectional dimension has no practical effect on the beam solution. A similar analysis can be performed to estimate the change in the height of the beam.
When the signs of \(z\) and \(y\) coordinates is properly taken into account, the present calculations predict the following change in the shape of the cross-section.
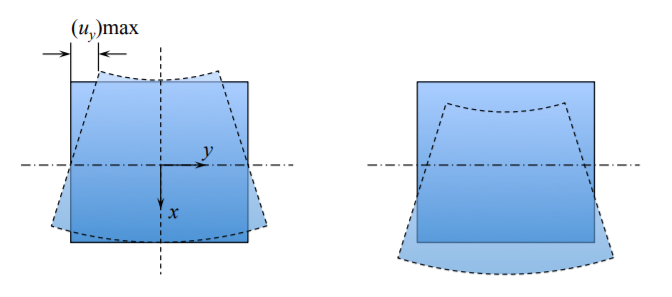
The anticlastic deformation can be easily seen by bending a rubber eraser, which is a very short beam. We can conclude the present section that the internal inconsistencies of the beam theory do not produce any significant errors in engineering applications. Therefore, one can safely assume that the cross-section of the beam does not deform and only moves as a rigid body with the increasing beam deflections.


