5.2: Solution for a Beam on Roller Support

Last updated
Save as PDF

Page ID: 21498

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Consider first case 1. From the constitutive equation, zero axial force beams that there is no extension of the beam axis, \(\epsilon^{\circ} = 0\). Then, from Equation (5.1.1)

\[\frac{du}{dx} = \frac{1}{2}\left(\frac{dw}{dx}\right)^2 \label{5.2.1}\]

At the same time, the nonlinear term in the vertical equilibrium vanishes and the beam response is governed by the linear differential equation

\[EI\frac{d^4w}{dx^4} = q(x)\]

which is identical to the one derived for the infinitesimal deflections. As an example, consider the pin-pin supported beam under mid-span point load. From Equations (4.3.7) and (4.3.8), the deflection profile is

\[w(x) = w_o \left[ 3 \frac{x}{l} − 4\left(\frac{x}{l}\right)^3\right]\]

and the slope is

\[\frac{dw}{dx} = \frac{w_o}{l}\left[3 − 12\left(\frac{x}{l}\right)^2\right]\]

where \(w_o\) is the central deflection of the beam. Now, Equation \ref{5.2.1} can be used to calculate relative horizontal displacement \(\Delta u\). Integrating Equation \ref{5.2.1} in the limits \((0, l)\) gives

\[\int_{0}^{l} \frac{du}{dx} dx= u|_{0}^{l} = u(l) − u(0) = \Delta u = − \int_{0}^{l} \frac{1}{2} \left( \frac{dw}{dx}\right)^2 dx\]

The result of the integration is

\[\Delta u \approx 7 \frac{w_{o}^2}{l}\]

In order to get a physical sense of the above result, the vertical and horizontal displacements are normalized by the thickness \(h\) of the beam

\[\frac{\Delta u}{h} = \frac{7}{l/h} \left(\frac{w_{o}}{h}\right)^2\]

For a beam with \(\frac{l}{h} = 21\), the result

\[\frac{\Delta u}{h} = \frac{1}{3} \left(\frac{w_{o}}{h}\right)^2\]

is ploted in Figure (\(\PageIndex{1}\)).

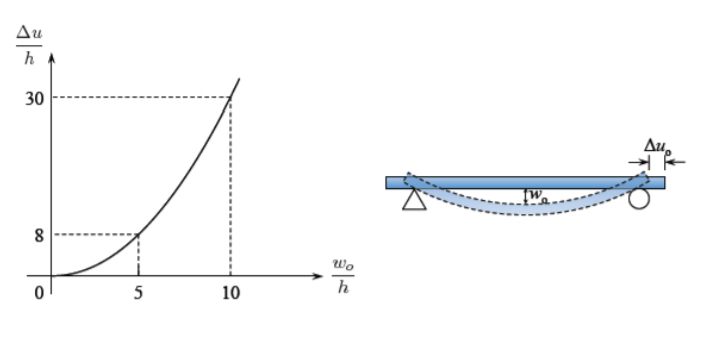
5.2.1.png — Figure \(\PageIndex{1}\): Sliding of a beam from the roller support.

It is seen that the amount of sliding in the horizontal direction can be very large compared to the thickness.

To summarize the results, the roller supported beam can be treated as a classical beam even though the displacements and rotations are large (moderate). The solution of the linear differential equation can then be used a posteriori to determine the magnitude of sliding. The analysis of fully restrained beam is much more interesting and difficult. This is the subject of the next section.