5.1: Closed-Form Solutions
- Page ID
- 44545
Introduction
During most of its historical development, the science of Mechanics of Materials relied principally on closed-form (not computational) mathematical theorists. Much of their work represents mathematical intuition and skill of a very high order, challenging even for advanced researchers of today. This theory is taught primarily in graduate subjects, but is outlined here both to provide some background that will be useful in the Module on Fracture and as a preliminary introduction to these more advanced subjects.
Governing equations
We have earlier shown (see Module 9) how the spatial gradients of the six Cauchy stresses are related by three equilibrium equations that can be written in pseudovector form as
\[L^T \sigma = 0\]
These are augmented by six constitutive equations which can be written for linear elastic materials as (see Module 11)
\[\sigma = D \epsilon\]
and six kinematic or strain-displacement equations (Module 8)
\[\sigma = Lu\]
These fifteen equations must be satisfied by the fifteen independent functions (three displacements \(u\), six strains \(\epsilon\), and six stresses \(\sigma\)). These functions must also satisfy boundary conditions on displacement
\[u = \hat{u} \text{ on } \Gamma_u\]
where \(\Gamma_u\) is the portion of the boundary on which the displacements \(u = \hat{u}\) are prescribed. The remainder of the boundary must then have prescribed tractions \(T = \hat{T}\), on which the stresses must satisfy Cauchy’s relation:
\[\sigma \hat{n} = \hat{T} \text{ on } \Gamma_T\]
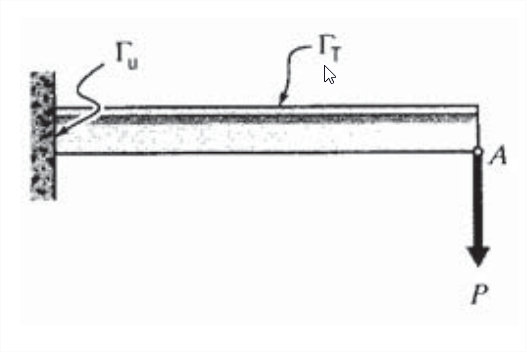
In the familiar cantilevered beam shown in Figure \(\PageIndex{1}\), the region of the beam at the wall constitutes \(\Gamma_u\), having specified (zero) displacement and slope. All other points on the beam boundary make up \(\Gamma_T\), with a load of \(P\) at the loading point \(A\) and a specified load of zero elsewhere.
With structures such as the beam that have simple geometries, solutions can be obtained by the direct method we have used in earlier modules: an expression for the displacements is written, from which the strains and stresses can be obtained, and the stresses then balanced against the externally applied loads. (Exercise \(\PageIndex{2}\) provides another example of this process.) In situations not having this geometrical simplicity, the analyst must carry out a mathematical solution, seeking functions of stress, strain and displacement that satisfy both the governing equations and the boundary conditions.
Currently, practical problems are likely to be solved by computational approximation, but it is almost always preferable to obtain a closed-form solution if at all possible. The mathematical result will show the functional importance of the various parameters, such as loading condi- tions or material properties, in a way a numerical solution cannot, and is therefore more useful in guiding design decisions. For this reason, the designer should always begin an analysis of load-bearing structures by searching for closed-form solutions of the given, or similar, problem. Several compendia of such solutions are available, the book by Roark(W.C. Young, Roark’s Formulas for Stress and Strain, McGraw-Hill, New York, 1989.) being a useful example.
However, there is always a danger in performing this sort of "handbook engineering" blindly, and this section is intended partly to illustrate the mathematical concepts that underlie many of these published solutions. It is probably true that most of the problems that can be solved mathematically have already been completed; these are the classical problems of applied mechanics, and they often require a rather high level of mathematical sophistication. The classic text by Timoshenko and Goodier(S. Timoshenko and J.N. Goodier, Theory of Elasticity, McGraw-Hill, New York, 1951.) is an excellent source for further reading in this area.
The Airy stress function
Expanding the kinematic or strain-displacement equations (Equation 5.1.3) in two dimensions gives the familiar forms:
\[\begin{array} {rcl} {\epsilon_x} & = & {\dfrac{\partial u}{\partial x}} \\ {\epsilon_y} & = & {\dfrac{\partial v}{\partial y}} \\ {\gamma_{xy}} & = & {\dfrac{\partial v}{\partial x} + \dfrac{\partial u}{\partial y}} \end{array}\]
Since three strains \((\epsilon_x, \epsilon_y, \gamma_{xy})\) are written in terms of only two displacements \((u,v)\), they cannot be specified arbitrarily; a relation must exist between the three strains. If \(\epsilon_x\) is differentiated twice by \(dx, \epsilon_y\) twice by \(dy\), and \(\gamma_{xy}\) by \(dx\) and then \(dy\) we have directly
\[\dfrac{\partial^2 \epsilon_x}{\partial y^2} + \dfrac{\partial^2 \epsilon_y}{\partial x^2} = \dfrac{\partial^2 \gamma_{xy}}{\partial x \partial y}\]
In order for the displacements to be so differentiable, they must be continuous functions, which means physically that the body must deform in a compatible manner, i.e. without developing cracks or overlaps. For this reason Equation 5.1.7 is called the compatibility equation for strains, since the continuity of the body is guaranteed if the strains satisfy it.
The compatibility equation can be written in terms of the stresses rather than the strains by recalling the constitutive equations for elastic plane stress:
\[\begin{array} {c} {\epsilon_x = \dfrac{1}{E} (\sigma_x - v \sigma_y)} \\ {\epsilon_y = \dfrac{1}{E} (\sigma_y - v \sigma_x)} \\ {\gamma_{xy} = \dfrac{1}{G} \tau_{xy} = \dfrac{2(1 + v)}{E} \tau_{xy}} \end{array}\]
Substituting these in Equation 5.1.7 gives
\[\dfrac{\partial^2}{\partial y^2} (\sigma_x - v \sigma_y) + \dfrac{\partial^2}{\partial x^2} (\sigma_y - v \sigma_x) = 2 (1 + v) \dfrac{\partial^2 \tau_{xy}}{\partial x \partial y}\]
Stresses satisfying this relation guarantee compatibility of strain.
The stresses must also satisfy the equilibrium equations, which in two dimensions can be written
\(\dfrac{\partial \sigma_x}{\partial x} + \dfrac{\partial \tau_{xy}}{\partial y} = 0\)
\[\dfrac{\partial \tau_{xy}}{\partial x} + \dfrac{\partial \sigma_y}{\partial y} = 0\]
As a means of simplifying the search for functions whose derivatives obey these rules, G.B. Airy (1801–1892) defined a stress function \(\phi\) from which the stresses could be obtained by differenti- ation:
\[\begin{array} {rcl} {\sigma_x} & = & {\dfrac{\partial^2 \phi}{\partial y^2}} \\ {\sigma_y} & = & {\dfrac{\partial^2 \phi}{\partial x^2}} \\ {\tau_{xy}} & = & {-\dfrac{\partial^2 \phi}{\partial x \partial y}} \end{array}\]
Direct substitution will show that stresses obtained from this procedure will automatically satisfy the equilibrium equations. This maneuver is essentially limited to two-dimensional problems, but with that proviso it provides a great simplification in searching for valid functions for the stresses.
Now substituting these into Equation 5.1.9, we have
\[\dfrac{\partial^4 \phi}{\partial x^4} + 2\dfrac{\partial^4 \phi}{\partial x^2 \partial y^2} + \dfrac{\partial^4 \phi}{\partial y^4} \equiv \nabla^2(\nabla^2 \phi) \equiv \nabla^4 \phi = 0\]
Any function \(\phi (x, y)\) that satisfies this relation will satisfy the governing relations for equilibrium, geometric compatibility, and linear elasticity. Of course, many functions could be written that satisfy the compatibility equation; for instance setting \(\phi = 0\) would always work. But to make the solution correct for a particular stress analysis, the boundary conditions on stress and displacement must be satisfied as well. This is usually a much more difficult undertaking, and no general solution that works for all cases exists. It can be shown, however, that a solution satisfying both the compatibility equation and the boundary conditions is unique; i.e. that it is the only correct solution.
Stresses around a circular hole
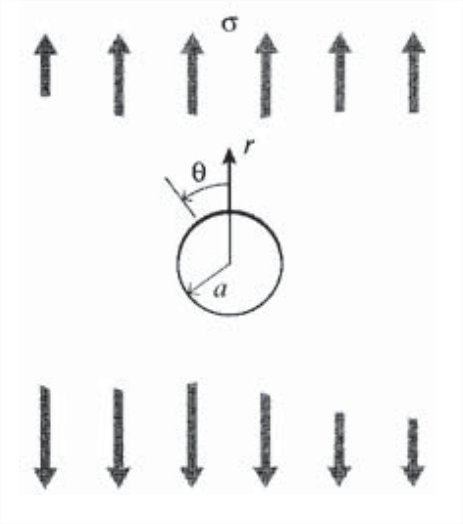
To illustrate the use of the Airy function approach, we will outline the important work of Kirsch(G. Kirsch, VDI, vol. 42, 1898; described in Timoshenko & Goodier, op. cit..), who obtained a solution for the influence on the stresses of a hole placed in the material. This is vitally important in analyzing such problems as rivet holes used in joining, and the effect of a manufacturing void in initiating failure. Consider a thin sheet as illustrated in Figure \(\PageIndex{2}\), infinite in lateral dimensions but containing a circular hole of radius \(a\), and subjected to a uniaxial stress \(\sigma\). Using circular \(r, \theta\) coordinates centered on the hole, the compatibility equation for \(\phi\) is
\[\nabla^4 \phi = (\dfrac{\partial^2}{\partial r^2} + \dfrac{1}{r}\dfrac{\partial}{\partial r} + \dfrac{1}{r^2}\dfrac{\partial^2}{\partial \theta^2}) (\dfrac{\partial^2 \phi}{\partial r^2} + \dfrac{1}{r}\dfrac{\partial \phi}{\partial r} + \dfrac{1}{r^2}\dfrac{\partial^2 \phi}{\partial \theta^2}) = 0\]
In these circular coordinates, the stresses are obtained from \(\phi\) as
\[\begin{array} {rcl} {\sigma_r} & = & {\dfrac{1}{r}\dfrac{\partial \phi}{\partial r} + \dfrac{1}{r^2}\dfrac{\partial^2 \phi}{\partial \theta^2}} \\ {\sigma_{\theta}} & = & {\dfrac{\partial^2 \phi}{\partial r^2}} \\ {\tau_{r\theta}} & = & {-\dfrac{\partial}{\partial r} (\dfrac{1}{r} \dfrac{\partial \phi}{\partial \theta})} \end{array}\]
We now seek a function \(\phi (r, \theta)\) that satisfies Equation 5.1.13 and also the boundary conditions of the problem. On the periphery of the hole the radial and shearing stresses must vanish, since no external tractions exist there:
\[\sigma_r = \tau_{r \theta} = 0, r = a\]
Far from the hole, the stresses must become the far-field value \(\sigma\); the Mohr procedure gives the radial and tangential stress components in circular coordinates as
\[\left \{ \begin{array} {rcl} {\sigma_r} & = & {\tfrac{\sigma}{2}(1 + \cos 2 \theta)} \\ {\sigma_{\theta}} & = & {\tfrac{\sigma}{2} (1 - \cos 2 \theta)} \\ {\tau_{r\theta}} & = & {\tfrac{\sigma}{2} \sin 2 \theta} \end{array} \right\} r \to \infty\]
Since the normal stresses vary circumferentially as \(\cos 2\theta\) (removing temporarily the \(\sigma/2\) factor) and the shear stresses vary as \(\sin 2\theta\), an acceptable stress function could be of the form
\[\phi = f(r) \cos 2 \theta\]
When this is substituted into Equation 5.1.13, an ordinary differential equation in \(f(r)\) is obtained:
\[\left(\frac{d^{2}}{d r^{2}}+\frac{1}{r} \frac{d}{d r}-\frac{4}{r^{2}}\right)\left(\frac{d^{2} f}{d r^{2}}+\frac{1}{r} \frac{d f}{d r}-\frac{4 f}{r^{2}}\right)=0\]
This has the general solution
\[f(r) = Ar^2 + Br^4 + C \dfrac{1}{r^2} + D\]
The stress function obtained from Eqns. 5.1.17 and 5.1.18 is now used to write expressions for the stresses according to Equation 5.1.14, and the constants determined using the boundary conditions in Eqns. 5.1.15 and 5.1.16; this gives
\[A=-\frac{\sigma}{4}, \quad B=0, \quad C=-\frac{a^{4} \sigma}{4}, \quad D=\frac{a^{2} \sigma}{2}\]
Substituting these values into the expressions for stress and replacing the \(\sigma /2\) that was temporarily removed, the final expressions for the stresses are
\[\begin{array} {rcl} {\sigma_r} & = & {\dfrac{\sigma}{2} (1 - \dfrac{a^2}{r^2}) + \dfrac{\sigma}{2} (1 + \dfrac{3a^4}{r^4} - \dfrac{4a^2}{r^2}) \cos 2 \theta} \\ {\sigma_{\theta}} & = & {\dfrac{\sigma}{2} (1 + \dfrac{a^2}{r^2}) - \dfrac{\sigma}{2} (1 + \dfrac{3a^4}{r^4}) \cos 2 \theta} \\ {\tau_{r \theta}} & = & {-\dfrac{\sigma}{2} (1 - \dfrac{3a^4}{r^4} + \dfrac{2a^2}{r^2}) \sin 2 \theta} \end{array}\]
As seen in the plot of Figure \(\PageIndex{1}\), the stress reaches a maximum value of \((\sigma_{\theta})_{\max} = 3\sigma\) at the periphery of the hole (\(r = a\)), at a diametral position transverse to the loading direction (\(\theta = \pi /2\)). The stress concentration factor, or SCF, for this problem is therefore 3. The \(x\)-direction stress falls to zero at the position \(\theta = \pi /2\), \(r = a\), as it must to satisfy the stress-free boundary condition at the periphery of the hole.
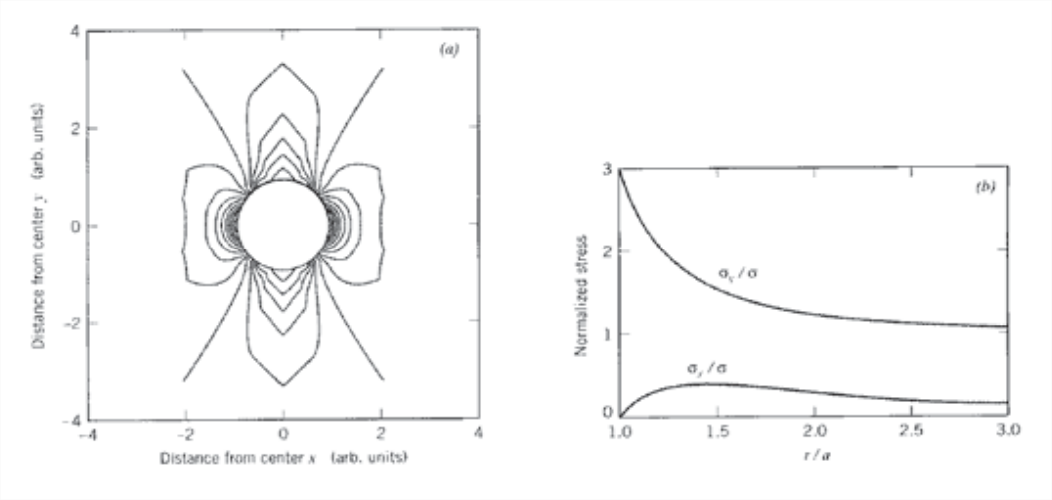
Note that in the case of a circular hole the SCF does not depend on the size of the hole: any hole, no matter how small, increases the local stresses near the hole by a factor of three. This is a very serious consideration in the design of structures that must be drilled and riveted in assembly. This is the case in construction of most jetliner fuselages, the skin of which must withstand substantial stresses as the differential cabin pressure is cycled by approximately 10 psig during each flight. The high-stress region near the rivet holes has a dangerous propensity to incubate fatigue cracks, and several catastrophic aircraft failures have been traced to exactly this cause.
Note also that the stress concentration effect is confined to the region quite close to the hole, with the stresses falling to their far-field values within three or so hole diameters. This is a manifestation of St. Venant’s principle(The French scientist Barr ́e de Saint-Venant (1797–1886) is one of the great pioneers in mechanics of materials.), which is a common-sense statement that the influence of a perturbation in the stress field is largely confined to the region of the disturbance. This principle is extremely useful in engineering approximations, but of course the stress concentration near the disturbance itself must be kept in mind.
When at the beginning of this section we took the size of the plate to be "infinite in lateral extent," we really meant that the stress conditions at the plate edges were far enough away from the hole that they did not influence the stress state near the hole. With the Kirsch solution now in hand, we can be more realistic about this: the plate must be three or so times larger than the hole, or the Kirsch solution will be unreliable.
Complex functions
In many problems of practical interest, it is convenient to use stress functions as complex functions of two variables. We will see that these have the ability to satisfy the governing equations automatically, leaving only adjustments needed to match the boundary conditions. For this reason, complex-variable methods play an important role in theoretical stress analysis, and even in this introductory treatment we wish to illustrate the power of the method. To outline a few necessary relations, consider \(z\) to be a complex number in Cartesian coordinates \(x\) and \(y\) or polar coordinates \(r\) and \(\theta\) as
\[z = x + iy = r^{i \theta}\]
where \(i = \sqrt{-1}\). An analytic function \(f(z)\) is one whose derivatives depend on \(z\) only, and takes the form
\[f(z) = \alpha + i \beta\]
where \(\alpha\) and \(\beta\) are real functions of \(x\) and \(y\). It is easily shown that \(\alpha\) and \(\beta\) satisfy the Cauchy-Riemann equations:
\[\dfrac{\partial \alpha}{\partial x} = \dfrac{\partial \beta}{\partial y}\ \ \ \ \ \dfrac{\partial \alpha}{\partial y} = -\dfrac{\partial \beta}{\partial x}\]
If the first of these is differentiated with respect to \(x\) and the second with respect to \(y\), and the results added, we obtain
\[\dfrac{\partial^2 \alpha}{\partial x^2} + \dfrac{\partial^2 \alpha}{\partial y^2} \equiv \nabla^2 \alpha = 0\]
This is Laplace’s equation, and any function that satisfies this equation is termed a harmonic function. Equivalently, \(\alpha\) could have been eliminated in favor of \(\beta\) to give \(\nabla^2 \beta = 0\), so both the real and imaginary parts of any complex function provide solutions to Laplace’s equation. Now consider a function of the form \(x \psi\), where \(\psi\) is harmonic; it can be shown by direct differentiation that
\[\nabla^4 (x \psi) = 0\]
i.e. any function of the form \(x\psi\), where \(\psi\) is harmonic, satisfies Equation 5.1.12, and many thus be used as a stress function. Similarly, it can be shown that \(y \psi\) and \((x^2 + y^2) \psi = r^2 \psi\) are also suitable, as is \(\psi\) itself. In general, a suitable stress function can be obtained from any two analytic functions \(\psi\) and \(\chi\) according to
\[\phi = \text{Re} [(x - iy) \psi (z) + \chi (z)]\]
where "\(\text{Re}\)" indicates the real part of the complex expression. The stresses corresponding to this function \(\phi\) are obtained as
\[\begin{array} {rcl} {\sigma_x + \sigma_y} & = & {4 \text{Re} \psi' (z)} \\ {\sigma_y - \sigma_x + 2 i \tau_{xy}} & = & {2 [\bar{z} \psi '' (z) + \chi '' (z)]} \end{array}\]
where the primes indicate differentiation with respect to \(z\) and the overbar indicates the conjugate function obtained by replacing \(i\) with \(-i\); hence \(\bar{z} = x - iy\).
Stresses around an elliptical hole
In a development very important to the theory of fracture, Inglis(C.E. Inglis, "Stresses in a Plate Due to the Presence of Cracks and Sharp Corners," Transactions of the Institution of Naval Architects, Vol. 55, London, 1913, pp. 219–230.) used complex potential functions to extend Kirsch’s work to treat the stress field around a plate containing an elliptical rather than circular hole. This permits crack-like geometries to be treated by making the minor axis of the ellipse small. It is convenient to work in elliptical \(\alpha, \beta\) coordinates, as shown in Figure 4, defined as
\[x = c \cosh \alpha \cos \beta, y = c \sin h \alpha \sin \beta\]
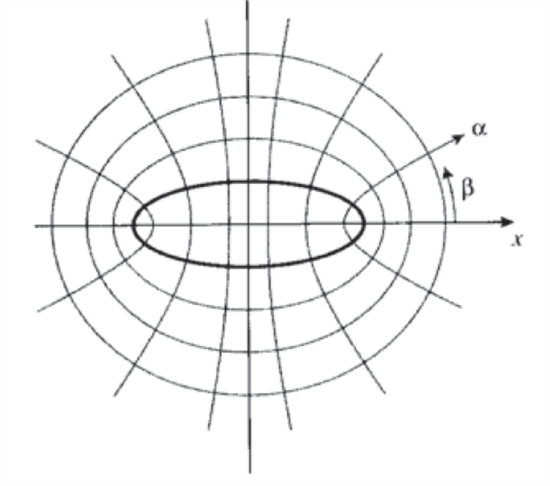
where \(c\) is a constant. If \(\beta\) is eliminated this is seen in turn to be equivalent to
\[\dfrac{x^2}{\cosh^2 \alpha} + \dfrac{y^2}{\sinh^2 \alpha} = c^2\]
On the boundary of the ellipse \(\alpha = \alpha_0\), so we can write
\[c \cosh \alpha_0 = a, c \sinh \alpha_0 = b\]
where \(a\) and \(b\) are constants. On the boundary, then
\[\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1\]
which is recognized as the Cartesian equation of an ellipse, with \(a\) and \(b\) being the major and minor radii. The elliptical coordinates can be written in terms of complex variables as
\[z = c \cosh \zeta, \ \ \ \ \zeta = \alpha + i \beta\]
As the boundary of the ellipse is traversed, \(\alpha\) remains constant at \(\alpha_0\) while \(\beta\) varies from 0 to \(2\pi\). Hence the stresses must be periodic in \(\beta\) with period \(2\pi\), while becoming equal to the far-field uniaxial stress \(\sigma_y = \sigma, \sigma_x = \tau_{xy} = 0\) far from the ellipse; Equation 5.1.26 then gives
\[\left \{ \begin{array} {rcl} {4 \text{Re} \psi ' (z)} & = & {\sigma} \\ {2[\bar{z} \psi '' (z) + \chi '' (z)]} & = & {\sigma} \end{array} \right \} \zeta \to \infty\]
These boundary conditions can be satisfied by potential functions in the forms
\(\begin{array} {rcl} {4 \psi (z)} & = & {Ac \cosh \zeta + Bc \sinh \zeta} \\ {4 \chi (z)} & = & {Cc^2 \zeta + Dc^2 \cosh 2 \zeta + Ec^2 \sinh 2 \zeta} \end{array}\)
where \(A,B,C,D,E\) are constants to be determined from the boundary conditions. When this is done the complex potentials are given as
\[4 \psi(z)=\sigma c\left[\left(1+e^{2 \alpha_{0}}\right) \sinh \zeta-e^{2 \alpha_{0}} \cosh \zeta\right]\]
\[4 \chi(z)=-\sigma c^{2}\left[\left(\cosh 2 \alpha_{0}-\cosh \pi\right) \zeta+\frac{1}{2} e^{2 \alpha_{0}}-\cosh 2\left(\zeta-\alpha_{0}-i \frac{\pi}{2}\right)\right]\]
The stresses \(\sigma_x, \sigma_y\), and \(\tau_{xy}\) can be obtained by using these in Eqns. 5.1.26. However, the amount of labor in carrying out these substitutions isn’t to be sneezed at, and before computers were generally available the Inglis solution was of somewhat limited use in probing the nature of the stress field near crack tips.
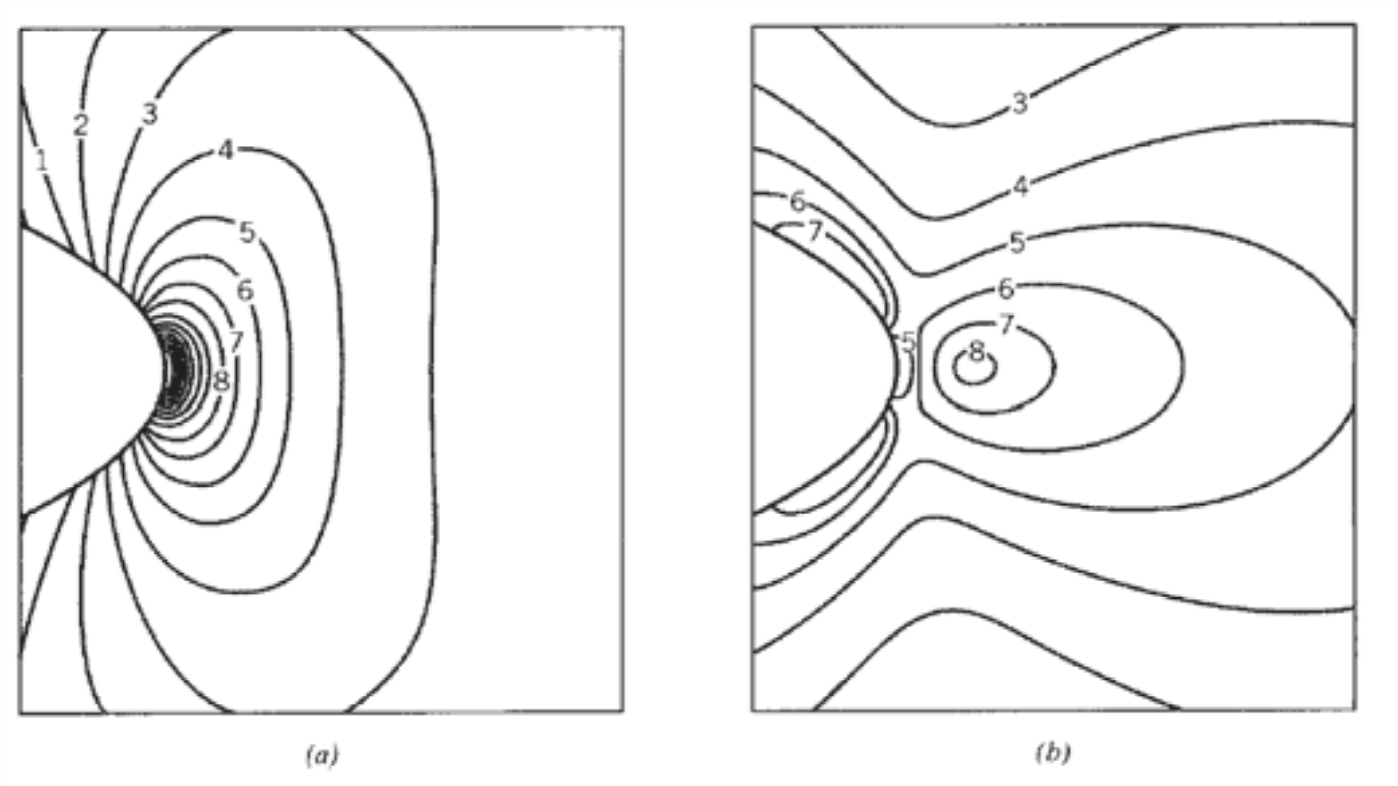
Figure 5: Stress field in the vicinity of an elliptical hole, with uniaxial stress applied in \(y\)-direction. (a) Contours of \(\sigma_y\), (b) Contours of \(\sigma_x\).
Figure 5 shows stress contours computed by Cook and Gordon(J.E. Gordon, The Science of Structures and Materials, Scientific American Library, New York, 1988.) from the Inglis equations. A strong stress concentration of the stress \(\sigma_y\) is noted at the periphery of the hole, as would be expected. The horizontal stress \(\sigma_x\) goes to zero at this same position, as it must to satisfy the boundary conditions there. Note however that \(\sigma_x\) exhibits a mild stress concentration (one fifth of that for \(\sigma_y\), it turns out) a little distance away from the hole. If the material has planes of weakness along the \(y\) direction, for instance as between the fibrils in wood or many other biological structures, the stress \(\sigma_x\) could cause a split to open up in the \(y\) direction just ahead of the main crack. This would act to blunt and arrest the crack, and thus impart a measure of toughness to the material. This effect is sometimes called the Cook-Gordon toughening mechanism.
The mathematics of the Inglis solution are simpler at the surface of the elliptical hole, since here the normal component \(\sigma_{\alpha}\) must vanish. The tangential stress component can then be computed directly:
\[\left(\sigma_{\beta}\right)_{\alpha=\alpha_{0}}=\sigma e^{2 \alpha_{0}}\left[\frac{\sinh 2 \alpha_{0}\left(1+e^{-2 \alpha_{0}}\right)}{\cosh 2 \alpha_{0}-\cos 2 \beta}-1\right]\]
The greatest stress occurs at the end of the major axis \((\cos 2 \beta = 1)\):
\[(\sigma_{\beta})_{\beta = 0, \pi} = \sigma_y = \sigma (1 + 2 \dfrac{a}{b})\]
This can also be written in terms of the radius of curvature \(\rho\) at the tip of the major axis as
\[\sigma_y = \sigma (1 + 2 \sqrt{\dfrac{a}{\rho}})\]
This result is immediately useful: it is clear that large cracks are worse than small ones (the local stress increases with crack size \(a\)), and it is also obvious that sharp voids (decreasing \(\rho\)) are worse than rounded ones. Note also that the stress \(\sigma_y\) increases without limit as the crack becomes sharper (\(\rho \to 0\)), so the concept of a stress concentration factor becomes difficult to use for very sharp cracks. When the major and minor axes of the ellipse are the same (\(b = a\)), the result becomes identical to that of the circular hole outlined earlier.
Stresses near a sharp crack
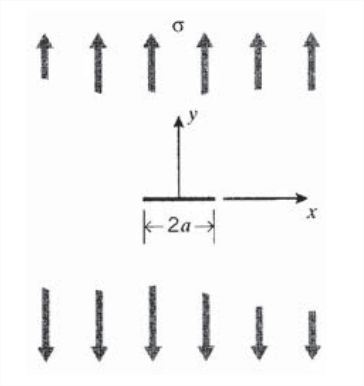
Figure 6: Sharp crack in an infinite sheet.
The Inglis solution is difficult to apply, especially as the crack becomes sharp. A more tractable and now more widely used approach was developed by Westergaard(Westergaard, H.M., "Bearing Pressures and Cracks," Transactions, Am. Soc. Mech. Engrs., Journal of Applied Mechanics, Vol. 5, p. 49, 1939.), which treats a sharp crack of length \(2a\) in a thin but infinitely wide sheet (see Figure 6). The stresses that act perpendicularly to the crack free surfaces (the crack "flanks") must be zero, while at distances far from the crack they must approach the far-field imposed stresses. Consider a harmonic function \(\phi (z)\), with first and second derivatives \(\phi '(z)\) and \(\phi '' (z)\), and first and second integrals \(\bar{\phi} (z)\) and \(\bar{\bar{\phi}}(z)\). Westergaard constructed a stress function as
\[\Phi = \text{Re} \bar{\bar{\phi}} (z) + y \text{Im} \bar{\phi} (z)\]
It can be shown directly that the stresses derived from this function satisfy the equilibrium, compatibility, and constitutive relations. The function \(\phi (z)\) needed here is a harmonic function such that the stresses approach the far-field value of \(\sigma\) at infinity, but are zero at the crack flanks except at the crack tip where the stress becomes unbounded:
\(\sigma_y = \begin{cases} \sigma, x \to \pm \infty, -a < x < + a,y = 0 \\ \infty, x = \pm \infty \end{cases}\)
These conditions are satisfied by complex functions of the form
\[\phi (z) = \dfrac{\sigma}{\sqrt{1 - a^2/z^2}}\]
This gives the needed singularity for \(z = \pm a\), and the other boundary conditions can be verified directly as well. The stresses are now found by suitable differentiations of the stress function; for instance
\(\sigma_y = \dfrac{\partial^2 \Phi}{\partial x^2} = \text{Re} \phi (z) + y \text{Im} \phi ' (z)\)
In terms of the distance \(r\) from the crack tip, this becomes
\[\sigma_y = \sigma \sqrt{\dfrac{a}{2r}} \cdot \cos \dfrac{\theta}{2} (1 + \sin \dfrac{\theta}{2} \sin \dfrac{3\theta}{2}) + \cdots\]
where these are the initial terms of a series approximation. Near the crack tip, when \(r \ll a\), we can write
\[(\sigma_y)_{y = 0} = \sigma \sqrt{\dfrac{a}{2r}} \equiv \dfrac{K}{\sqrt{2 \pi r}}\]
where \(K = \sigma \sqrt{\pi a}\) is the stress intensity factor, with units of \(Nm^{-3/2}\) or \(\text{psi} \sqrt{\text{in}}\). (The factor \(\pi\) seems redundant here since it appears to the same power in both the numerator and denominator, but it is usually included as written here for agreement with the older literature.) We will see in the Module on Fracture that the stress intensity factor is a commonly used measure of the driving force for crack propagation, and thus underlies much of modern fracture mechanics. The dependency of the stress on distance from the crack is singular, with a \(1/\sqrt{r}\) dependency. The K factor scales the intensity of the overall stress distribution, with the stress always becoming unbounded as the crack tip is approached.
Exercise \(\PageIndex{1}\)
Expand the governing equations (Eqns. 5.1.1 - 5.1.3) in two Cartesian dimensions. Identify the unknown functions. How many equations and unknowns are there?
Exercise \(\PageIndex{2}\)
Consider a thick-walled pressure vessel of inner radius \(r_i\) and outer radius \(r_o\), subjected to an internal pressure \(p_i\) and an external pressure \(p_o\).
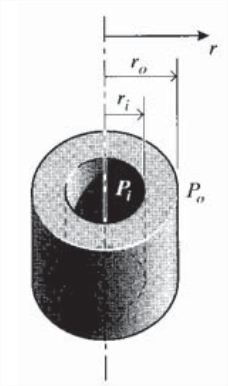
Assume a trial solution for the radial displacement of the form \(u(r) = Ar + B/r\); this relation can be shown to satisfy the governing equations for equilibrium, strain-displacement, and stress-strain governing equations.
(a) Evaluate the constants \(A\) and \(B\) using the boundary conditions
\[\sigma_r = -p_i @ r = r_i, \sigma_r = -p_0 @ r = r_o\]
(b) Then show that
\[\sigma_{r}(r)=-\frac{p_{i}\left[\left(r_{o} / r\right)^{2}-1\right]+p_{o}\left[\left(r_{o} / r_{i}\right)^{2}-\left(r_{o} / r\right)^{2}\right]}{\left(r_{o} / r_{i}\right)^{2}-1}\]
Exercise \(\PageIndex{3}\)
Justify the boundary conditions given in Eqns. 5.1.14 for stress in circular coordinates (\(\sigma_r, \sigma_{\theta}, \tau_{xy}\)) appropriate to a uniaxially loaded plate containing a circular hole.
Exercise \(\PageIndex{4}\)
Show that the Airy function \(\phi (x, y)\) defined by Eqns. 5.1.11 satisfies the equilibrium equations.
Exercise \(\PageIndex{5}\)
Show that stress functions in the form of quadratic or cubic polynomials \((\phi = a_2 x^2 + b_2 xy + c_2 y^2\) and \(\phi = a_3 x^3 + b_3 x^2 y + c_3 xy^2 + d_3 y^3\)) automatically satisfy the governing relation \(\nabla^4 \phi = 0\).
Exercise \(\PageIndex{6}\)
Write the stresses \(\sigma_x, \sigma_y, \tau_{xy}\) corresponding to the quadratic and cubic stress functions of the previous problem.
Exercise \(\PageIndex{7}\)
Choose the constants in the quadratic stress function of the previous two problems so as to represent (a) simple tension, (b) biaxial tension, and (c) pure shear of a rectangular plate.
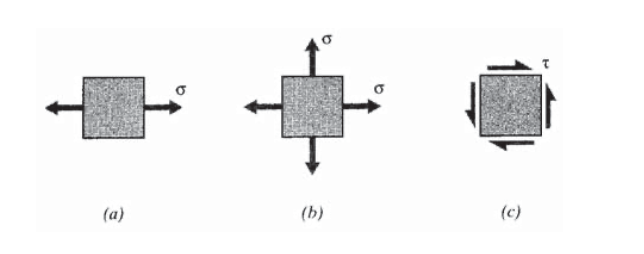
Exercise \(\PageIndex{8}\)
Choose the constants in the cubic stress function of the previous problems so as to represent pure bending induced by couples applied to vertical sides of a rectangular plate.

Exercise \(\PageIndex{9}\)
Consider a cantilevered beam of rectangular cross section and width \(b = 1\), loaded at the free end (\(x = 0\)) with a force \(P\). At the free end, the boundary conditions on stress can be written \(\sigma_x = \sigma_y = 0\), and
\(\int_{-h/2}^{h/2} \tau_{xy} \ dy = P\)
The horizontal edges are not loaded, so we also have that \(\tau_{xy} = 0\) at \(y = \pm h/2\).
(a) Show that these conditions are satisfied by a stress function of the form
\(\phi = b_2 xy + d_4 xy^3\)
(b) Evaluate the constants to show that the stresses can be written
\[\sigma_{x}=\frac{P x y}{I}, \quad \sigma_{y}=0, \quad \tau_{x y}=\frac{P}{2 I}\left[\left(\frac{h}{2}\right)^{2}-y^{2}\right]\]
in agreement with the elementary theory of beam bending (Module 13).