5.2: Experimental Solutions

Introduction

As was seen in previous modules, stress analysis even of simple-appearing geometries can lead to complicated mathematical maneuvering. Actual articles -- engine crankshafts, medical prostheses, tennis rackets, etc. -- have boundary shapes that cannot easily be described mathematically, and even if they were it would be extremely difficult to fit solutions of the governing equations to them. One approach to this impasse is the experimental one, in which we seek to construct a physical laboratory model that somehow reveals the stresses in a measurable way.

It is the nature of forces and stresses that they cannot be measured directly. It is the effect of a force that is measurable: when we weigh an object on a spring scale, we are actually measuring the stretching of the spring, and then calculating the force from Hooke's law. Experimental stress analysis, then, is actually experimental strain analysis. The difficulty is that strains in the linear elastic regime are almost always small, on the order of 1% or less, and the art in this field is that of detecting and interpreting small displacements. We look for phenomena that exhibit large and measurable changes due to small and difficult-to-measure displacements. There a number of such techniques, and three of these will be outlined brief y in the sections to follow. A good deal of methodology has been developed around these and other experimental methods, and both further reading(Manual on Experimental Stress Analysis, Third Edition, Society of Experimental Stress Analysis (now Society of Experimental Mechanics), 1978.) and laboratory practice would be required to put become competent in this area.

Strain gages

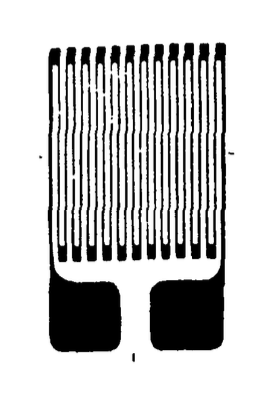
The term "strain gage" usually refers to a thin wire or foil, folded back and forth on itself and bonded to the specimen surface as seen in Figure 1, that is able to generate an electrical measure of strain in the specimen. As the wire is stretched along with the specimen, the wire's electrical resistance \(R\) changes both because its length \(L\) is increased and its cross-sectional area \(A\) is reduced. For many resistors, these variables are related by the simple expression discovered in 1856 by Lord Kelvin:

\(R = \dfrac{\rho L}{A}\)

Figure 1: Wire resistance strain gage.

where here \(\rho\) is the material's resistivity. To express the effect of a strain \(\epsilon = dL/L\) in the wire's long direction on the electrical resistance, assume a circular wire with \(A = \pi r^2\) and take logarithms:

The total differential of this expression gives

Since

\(\epsilon_r = \dfrac{dr}{r} = -v \dfrac{dL}{L}\)

then

\(\dfrac{dR}{R} = \dfrac{d \rho}{\rho} (1 + 2v) \dfrac{dL}{L}\)

P.W. Bridgeman (1882 - 1961) in 1929 studied the effect of volume change on electrical resistance and found these to vary proportionally:

\[\dfrac{d\rho}{\rho} = \alpha_R \dfrac{dV}{V}\]

where \(\alpha_R\) is the constant of proportionality between resistance change and volume change. Writing the volume change in terms of changes in length and area, this becomes

Hence

\[\dfrac{dR/R}{\epsilon} = (1 + 2v) + \alpha_R (1 - 2v)\]

This quantity is called the gage factor, GF. Constantan, a 45/55 nickel/copper alloy, has \(\alpha_R = 1.13\) and \(v = 0.3\), giving \(GF \approx 2.0\). This material also has a low temperature coefficient of resistivity, which reduces the temperature sensitivity of the strain gage.

Figure 2: Wheatstone bridge circuit for strain gages.

A change in resistance of only 2%, which would be generated by a gage with \(GF = 2\) at 1% strain, would not be noticeable on a simple ohmmeter. For this reason strain gages are almost always connected to a Wheatstone-bridge circuit as seen in Figure 2. The circuit can be adjusted by means of the variable resistance \(R_2\) to produce a zero output voltage \(V_{out}\) before strain is applied to the gage. Typically the gage resistance is approximately 350\(\Omega\) and the excitation voltage is near \(10V\). When the gage resistance is changed by strain, the bridge is unbalanced and a voltage appears on the output according to the relation

\(\dfrac{V_{out}}{V_{in}} = \dfrac{\Delta R}{2R_0}\)

where \(R_0\) is the nominal resistance of the four bridge elements. The output voltage is easily measured because it is a deviation from zero rather than being a relatively small change superimposed on a much larger quantity; it can thus be amplified to suit the needs of the data acquisition system.

Temperature compensation can be achieved by making a bridge element on the opposite side of the bridge from the active gage, say \(R_3\), an inactive gage that is placed near the active gage but not bonded to the specimen. Resistance changes in the active gage due to temperature will then be offset be an equal resistance change in the other arm of the bridge.

Figure 3: Cancellation of bending effects.

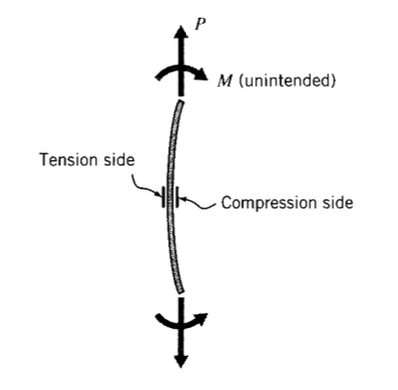
It is often difficult to mount a tensile specimen in the testing machine without inadvertently applying bending in addition to tensile loads. If a single gage were applied to the convex- outward side of the specimen, its reading would be erroneously high. Similarly, a gage placed on the concave-inward or compressive-tending side would read low. These bending errors can be eliminated by using an active gage on each side of the specimen as shown in Figure 3 and wiring them on the same side of the Wheatstone bridge, e.g. \(R_1\) and \(R_4\). The tensile component of bending on one side of the specimen is accompanied by an equal but compressive component on the other side, and these will generate equal but opposite resistance changes in \(R_1\) and \(R_4\). The effect of bending will therefore cancel, and the gage combination will measure only the tensile strain (with doubled sensitivity, since both \(R_1\) and \(R_4\) are active).

Figure 4: Strain rosette.

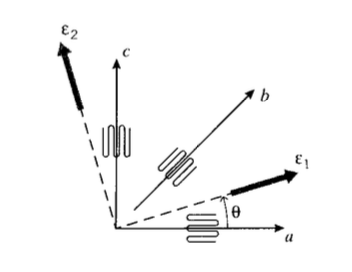
The strain in the gage direction can be found directly from the gage factor (Equation 5.2.1). When the direction of principal stress is unknown, strain gage rosettes are useful; these employ multiple gages on the same film backing, oriented in different directions. The rectangular three-gage rosette shown in Figure 4 uses two gages oriented perpendicularly, and a third gage oriented at 45\(^{\circ}\) to the first two.

Example \(\PageIndex{1}\)

A three-gage rosette gives readings \(\epsilon_0 = 150\mu\), \(\epsilon_{45} = 200 \mu\), and \(\epsilon_{90} = -100 \mu\) (here the \(\mu\) symbol indicates micrometers per meter). If we align the \(\epsilon_x\) and \(\epsilon_y\) axis along the 0\(^{\circ}\) and 90\(^{\circ}\) gage directions, then \(\epsilon_x\) and \(\epsilon_y\) are measured directly, since these are \(\epsilon_0\) and \(\epsilon_{90}\) respectively. To determine the shear strain \(\gamma_{xy}\), we use the rule for strain transformation to write the normal strain at 45\(^{\circ}\):

\(\epsilon_{45} = 200\mu = \epsilon_{x} \cos^2 45 + \epsilon_y \sin^2 45 + \gamma_{xy} \sin 45 \cos 45\)

Substituting the known values for \(\epsilon_x\) and \(\epsilon_y\), and solving,

\(\gamma_{xy} = 350 \mu\)

The principal strains can now be found as

The angle from the \(x\)-axis to the principal plane is

The stresses can be found from the strains from the material constitutive relations; for instance for steel with \(E = 205\) GPa and \(ν = .3\) the principal stress is

For the specific case of a 0-45-90 rosette, the orientation of the principal strain axis can be given directly by(M. Hetenyi, ed., Handbook of Experimental Stress Analysis, Wiley, New York, 1950.)

\[\tan 2 \theta = \dfrac{2 \epsilon_b - \epsilon_a - \epsilon_c}{\epsilon_a - \epsilon_c}\]

and the principal strains are

\[\epsilon_{1, 2} = \dfrac{\epsilon_a + \epsilon_c}{2} \pm \sqrt{\dfrac{(\epsilon_a - \epsilon_b)^2 + (\epsilon_b - \epsilon_c)^2}{2}}\]

Graphical solutions based on Mohr's circles are also useful for reducing gage output data.

Strain gages are used very extensively, and critical structures such as aircraft may be instrumented with hundreds of gages during testing. Each gage must be bonded carefully to the structure, and connected by its two leads to the signal conditioning unit that includes the excitation voltage source and the Wheatstone bridge. This can obviously be a major instrumentation chore, with computer-aided data acquisition and reduction a practical necessity.

Photoelasticity

Wire-resistance strain gages are probably the principal device used in experimental stress analysis today, but they have the disadvantage of monitoring strain only at a single location. Photoelasticity and moire methods, to be outlined in the following sections, are more complicated in concept and application but have the ability to provide full-field displays of the strain distribution. The intuitive insight from these displays can be so valuable that it may be unnecessary to convert them to numerical values, although the conversion can be done if desired.

Figure 5: Light propagation.

Photoelasticity employs a property of many transparent polymers and inorganic glasses called birefringence. To explain this phenomenon, recall the definition of refractive index, \(n\), which is the ratio of the speed of light \(v\) in the medium to that in vacuum \(c\):

\[n = \dfrac{v}{c}\]

As the light beam travels in space (see Figure 5), its electric field vector \(E\) oscillates up and down at an angular frequency \(\omega\) in a fixed plane, termed the plane of polarization of the beam. (The wavelength of the light is \(\lambda = 2\pi c/\omega\).) A birefringent material is one in which the refractive index depends on the orientation of plane of polarization, and magnitude of the birefringence is the difference in indices:

\(\Delta n = n_{\perp} - n_{\parallel}\)

where \(n_{\perp}\) and \(n_{\parallel}\) are the refractive indices on the two planes. Those two planes that produce the maximum \(\Delta_n\) are the principal optical planes. As shown in Figure 6, a birefringent material can be viewed simplistically as a Venetian blind that resolves an arbitrarily oriented electric field vector into two components, one on each of the two principal optical planes, after which each component will transit the material at a different speed according to Equation 5.2.4. The two components will eventually exit the material, again traveling at the same speed but having been shifted in phase from one another by an amount related to the difference in transit times.

Figure 6: Venetian-blind model of birefringence.

A photoelastic material is one in which the birefringence depends on the applied stress, and many such materials can be described to a good approximation by the stress-optical law

\[\Delta_n = C(\lambda) (\sigma_1 - \sigma_2)\]

where \(C\) is the stress-optical coefficient, and the quantity in the second parentheses is the difference between the two principal stresses in the plane normal to the light propagation direction; this is just twice the maximum shear stress in that plane. The stress-optical coefficient is generally a function of the wavelength \(\lambda\).

The stress distribution in an irregularly shaped body can be viewed by replicating the actual structure (probably scaled up or down in size for convenience) in a birefringent material such as epoxy. If the structure is statically determinate, the stresses in the model will be the same as that in the actual structure, in spite of the differences in modulus. To make the birefringence effect visible, the model is placed between crossed polarizers in an apparatus known as a polariscope. (Polarizers such as Polaroid, a polymer sheet containing oriented iodide crystals, are essentially just birefringent materials that pass only light polarized in the polarizer's principal optical plane.)

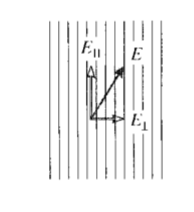
The radiation source can produce either conventional white (polychromatic) or filtered (monochromatic) light. The electric field vector of light striking the first polarizer with an arbitrary orientation can be resolved into two components as shown in Figure 7, one in the polarization direction and the other perpendicular to it. The polarizer will block the transverse component, allowing the parallel component to pass through to the specimen. This polarized component can be written

Figure 7: The circular polariscope.

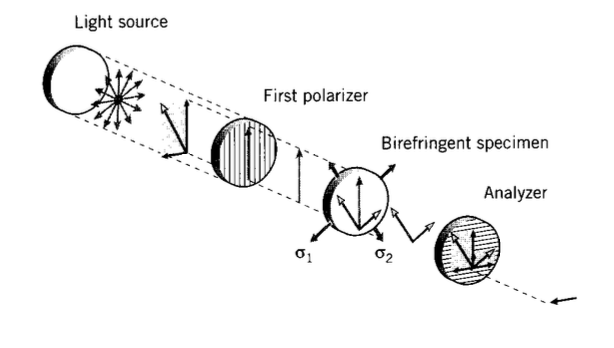
\(u_P = A \cos \omega t\)

where \(u_P\) is the field intensity at time \(t\). The birefringent specimen will resolve this component into two further components, along each of the principal stress directions; these can be written as

\(u_1 = A \cos \alpha \cos \omega t\)

\(u_2 = A \sin \alpha \cos \omega t\)

where α is the (unknown) angle the principal stress planes makes with the polarization direction. Both of these new components pass through the specimen, but at different speeds as given by Equation 5.2.5. After traveling through the specimen a distance \(h\) with velocities \(v_1\) and \(v_2\), they emerge as

These two components then fall on the second polarizer, oriented at 90\(^{\circ}\) to the first and known as the analyzer. Each is again resolved into further components parallel and perpendicular to the analyzer axis, and the perpendicular components blocked while the parallel components passed through. The transmitted component can be written as

\(u_A = -u_1' \sin \alpha + u_2' \cos \alpha\)

This is of the form \(u_A = A' \sin (\omega t - \delta)\), where \(A'\) is an amplitude and \(\delta\) is a phase angle. Note that the amplitude is zero, so that no light will be transmitted, if either \(\alpha = 0\) or if

\[\dfrac{2 \pi c}{\lambda} ( \dfrac{h}{2v_1} - \dfrac{h}{2v_2} ) = 0, \pi, 2\pi, \cdots\]

The case for which \(\alpha = 0\) occurs when the principal stress planes are aligned with the polarizer-analyzer axes. All positions on the model at which this is true thus produce an extinction of the transmitted light. These are seen as dark bands called isoclinics, since they map out lines of constant inclination of the principal stress axes. These contours can be photographed at a sequence of polarization orientations, if desired, to give an even more complete picture of stress directions.

Positions of zero stress produce extinction as well, since then the retardation is zero and the two light components exiting the analyzer cancel one another. The neutral axis of a beam in bending, for instance, shows as a black line in the observed field. As the stress at a given location is increased from zero, the increasing phase shift between the two components causes the cancellation to be incomplete, and light is observed. Eventually, as the stress is increased still further, the retardation will reach \(\delta = \pi\), and extinction occurs again. This produces another dark fringe in the observed field. In general, alternating light areas and dark fringes are seen, corresponding to increasing orders of extinction.

Figure 8: Photoelastic patterns for stress around (a) a circular hole and (b) a sharp crack.

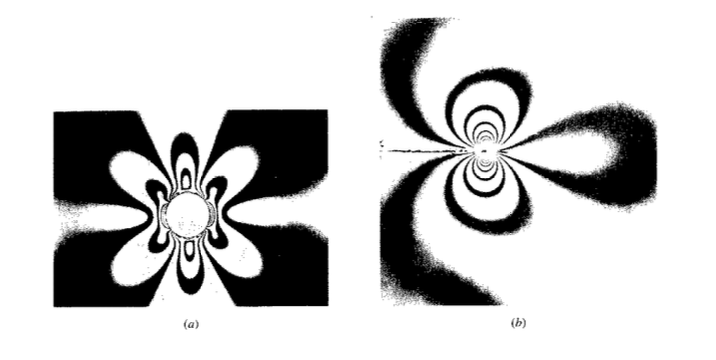
Close fringe spacing indicates a steep stress gradient, similar to elevation lines on a geographical contour map; Figure 8 shows the patterns around circular and a sharp-crack stress risers. It may suffice simply to observe the locations of high fringe density to note the presence of stress concentrations, which could then be eliminated by suitable design modifications (such as rounding corners or relocating abrupt geometrical discontinuities from high-stress regions). If white rather than monochromatic light is used, brightly colored lines rather than dark fringes are observed, with each color being the complement of that color that has been brought into extinction according to Equation 5.2.4. These bands of constant color are termed isochromatics.

Converting the fringe patterns to numerical stress values is usually straightforward but tedious, since the fringes are related to the stress difference \(\sigma_1 - \sigma_2\) rather than a single stress. At a free boundary, however, the stress components normal to the boundary must be zero, which means that the stress tangential to the boundary is a principal stress and is therefore given directly by the fringe order there. The reduction of photoelastic patterns to numerical values usually involves beginning at these free surfaces, and then working gradually into the interior of the body using a graphical procedure.

Moire

The term "moire" is spelled with a small "m" and derives not from someone's name but from the name of a silk fabric that shows patterns of light and dark bands. Bands of this sort are also developed by the superposition of two almost-identical gratings, such as might be seen when looking through two window screens slightly rotated from one another. Figure 9 demonstrates that fringes are developed if the two grids have different spacing as well as different orientations. The fringes change dramatically for even small motions or strains in the gratings, and this visual amplification of motion can be used in detecting and quantifying strain in the specimen.

Figure 9: Moire fringes developed by difference in line pitch (a) and line orientation (b). (Prof. Fu-Pen Chiang, SUNY-Stony Brook.)

As a simple illustration of moire strain analysis, assume a grating of vertical lines of spacing \(p\) (the \specimen" grating) is bonded to the specimen and that this is observed by looking through another \reference" grating of the same period but not bonded to the specimen. Now let the specimen undergo a strain, so that the specimen grating is stretched to a period of \(p'\). A dark fringe will appear when the lines from the two gratings superimpose, and this will occur when \(N(p' - p) = p\), since after \(N\) lines on the specimen grid the incremental gap (\(p' - p\)) will have accumulated to one reference pitch distance \(p\). The distance \(S\) between the fringes is then

\[S = Np' = \dfrac{pp'}{p' - p}\]

The normal strain \(\epsilon_x\) in the horizontal direction is now given directly from the fringe spacing as

\[\epsilon_x = \dfrac{p' - p}{p} = \dfrac{p}{S}\]

Fringes will also develop if the specimen grid undergoes a rotation relative to the reference grid: if the rotation is small, then

\(\dfrac{p}{S} = \tan \theta \approx \theta\)

\(S = \dfrac{p}{\theta}\)

This angle is also the shear strain \(\gamma_{xy}\), so

\[\gamma_{xy} = \theta = \dfrac{p}{\theta}\]

More generally, consider the interference fringes that develop between a vertical reference grid and an arbitrarily displaced specimen grid (originally vertical). The zeroth-order (\(N = 0\)) fringe is that corresponding to positions having zero horizontal displacement, the first-order (\(N = 1\)) fringe corresponds to horizontal motions of exactly one pitch distance, etc. The horizontal displacement is given directly by the fringe order as \(u = N_p\), from which the strain is given by

\[\epsilon_x = \dfrac{\partial u}{\partial x} = p \dfrac{\partial N}{\partial x}\]

so the strain is given as the slope of the fringe.

Similarly, a moire pattern developed between two originally horizontal grids, characterized by fringes \(N' = 0, 1, 2, \cdots\) gives the vertical strains:

\[\epsilon _y = \dfrac{\partial v}{\partial y} = \dfrac{\partial (N'p)}{\partial y} = p \dfrac{\partial N'}{\partial y}\]

The shearing strains are found from the slopes of both the \(u\)-field and \(v\)-field fringes:

\[\gamma_{xy} = p(\dfrac{\partial N}{\partial y} + \dfrac{\partial N'}{\partial x})\]

Figure 10 shows the fringes corresponding to vertical displacements around a circular hole in a plate subjected to loading in the \(y\)-direction. The vertical strain \(\epsilon_y\) is proportional to the \(y\)-distance between these fringes, each of which is a contour of constant vertical displacement. This strain is largest along the \(x\)-axis at the periphery of the hole, and smallest along the \(y\)-axis at the periphery of the hole.

Figure 10: Moire patterns of the vertical displacements of a bar with a hole under pure tension. (Prof. Fu-Pen Chiang, SUNY-Stony Brook.)

Exercise \(\PageIndex{1}\)

A \(0^{\circ}\)/\(45^{\circ}\)/\(90^{\circ}\) three-arm strain gage rosette bonded to a steel specimen gives readings \(\epsilon_0 = 175 \mu\), \(\epsilon_{45} =150\mu\), and \(\epsilon_{90} = -120\mu\). Determine the principal stresses and the orientation of the principal planes at the gage location.

Exercise \(\PageIndex{2}\)

Repeat the previous problem, but with gage readings \(\epsilon_0 = 150 \mu, \epsilon_{45} = 200 \mu\), and \(\epsilon_{90} = 125 \mu\).