Ferrimagnetism

Magnetic properties of materials are often utilized in advance technological devices such as superconductive Maglev trains, scanning electron microscopy, electron beam physical vapor deposition, and internal and external computer hard drives. There are five types of magnetism:

1. diamagnetism,
2. paramagnetism,
3. ferromagnetism,
4. antiferromagnetism, and
5. ferrimagnetism.

Each type of magnetism differs from the others because of differences in the composition and crystal structures of the materials, and how electrons within these materials respond to a magnetic field.

Introduction

Ferrimagnetism can be thought of as a combination of ferromagnetism and antiferromagnetism because of the many similarities between them, but it has important points of difference also. Similar to ferromagnets, ferrimagnets exhibit a spontaneous magnetic moment (i.e., a magnetic moment even in the absence of a magnetic field) and hysteresis below their Curie temperature, \(T_c\), and behave paramagnetically above the Curie temperature. On the other hand, similar to antiferromagnets, the magnetic moments of ferrimagnets align antiparallel to one another, the difference being that the net magnetic moment is non-zero. Ferrimagnetic materials are thus differentiated from ferromagnetic and antiferromagnetic materials by the arrangement of their magnetic moments, and the dependence of the resulting magnetic properties on temperature, which depend on the types of elements in the material, its crystal structure, and microstructural processing.

Ferrimagnetic materials are widely used in non-volatile memory devices such as hard drives, which utilize their ability to easily switch the spins of electrons and be magnetized. When a ferrimagnet inside a coil of conducting wire is rotate, current is generated, so they are also widely used in power motors and generators. Because ferrimagnets are electrically insulating, they are also widely used in high-frequency devices because no eddy currents are induced under AC fields.

Ferrimagnetic Materials

Unlike ferromagnetic materials, which are typically metals, ferrimagnetic materials are ceramics, in particular, ceramic oxides. The most widely used ferrimagnets in technological devices are materials known as ferrites. Ferrites are electrically insulating transitional-metal oxides with the general chemical formula MO·Fe₂·O₃, where M is a divalent ion such as Mn²⁺, Fe²⁺, Co²⁺, or Ni²⁺.

Ferrites are often prepared by standard ceramic processing techniques. In the case of NiO.Fe₂·O₃ powders of NiO and Fe₂O₃ are mixed together and pressed into the desired shape before sintering (firing) at high temperature to form a dense ceramic of the desired composition. This method provides a reliable way of forming a wide variety of shapes and sizes of ferrimagnetic materials for embedding into technological devices.

Magnetization of Ferrimagnetic Materials

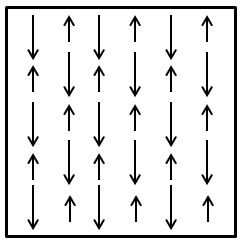
Ferrimagnetic materials contain magnetic moments aligned antiparallel to one another, as illustrated in the figure below, similar to antiferromagnetic materials. However, instead of having a zero net magnetic moment, different numbers of unpaired electrons in the component transition metals result do not cancel one another out, resulting in a spontaneous magnetization.

The figure below shows the ordering of magnetic ions in a ferrimagnetic lattice, with arrows pointing down being longer than those pointing up to indicate the relative size of the spin-up and spin-down moments. The result is a net magnetic moment in the down spin direction.

Figure \(\PageIndex{1}\): Magnetic ordering in a ferrimagnetic material.

The antiparallel magnetic moments in both ferrimagnetic and antiferromagnetic materials can be explained by the superexchange behavior that occurs in oxide materials. Using manganese oxide, MnO, as an example, in its crystal oxygen ions, O^2-, sit between manganese ions, Mn²⁺, as shown schematically in the figure below. Due to the different energy levels of the Mn and O orbitals, in order for bonding between the two ions to occur, the spin direction of one electron in Mn²⁺ is flipped to match that of the electron in the oxygen ion, thus forcing magnetic moments on either side of the molecule to be antiparallel to each other.

Figure \(\PageIndex{2}\): Initial transition of superexchange behavior in MnO where the magnetic moment of one electron of the left-side Mn³⁺ is flipped due to the down-spin of the electron in the leftmost orbital of the O^2- ion to which it bonds.

Figure \(\PageIndex{3}\): The result of superexchange behavior whereby all electrons of the left-side Mn³⁺ are rotated to be antiparallel to the right-side Mn³⁺, so that both match the spins of the bonding orbitals of the O^2- ion.

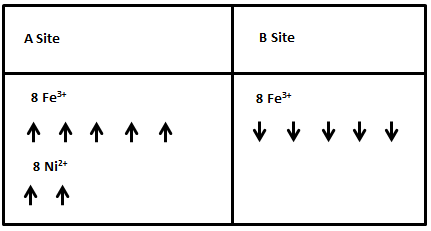
The spontaneous magnetization of ferrimagnetic materials originates from the non-zero net magnetic moments when filling up the d orbitals of transition metal ions according to Hund’s Rule. In the case of ferrites, which have what is known as an inverse spinel structure, the crystal structure can be thought of as consisting of two sublattices. Ions on sublattice A are tetrahedrally coordinated to neighboring oxide ions, while those on sublattice B are octahedrally coordinated (figure 4). Ions on each sublattice have their spins aligned in the same direction as one another. The magnetic moments of Fe³⁺ ions cancel each other out because there is the same number of ions on the A and B sublattices, but with their moments aligned in opposite directions.

In order for there to be magnetization in the material, the numbers of magnetic ions on each of the sublattices have to be different, so that not all magnetic moments are canceled out. Specifically, in order to create features of ferrimagnetism from A Site and B Site, interactions involving both sublattices must be considered: A-A, B-B, and A-B site interactions. Since A sites and B sites in the inverse spinel structure have different environments, the magnetization and the Weiss molecular fields are also not identical in magnitude. The total magnetization of the crystal can be expressed as the sum of magnetization on the A and B sublattices:

\[M_{total} = M_A+M_B \label{1}\]

where

\[M_A = \alpha n \mu_A \label{2a}\]

and

\[M_B = \alpha n \mu_B \label{2b}\]

Here n is the number of magnetic ions per unit volume, α is the faction of A ions, beta is the fraction of B ions, and µ_A and µ_B are the average magnetic moment of an A ion and B ion, respectively, in the direction of the field at temperature T.

Similarly, the Weiss molecular field, which is the internal interaction between localized moments, can be expressed in terms of the molecular field strengths from of A site ions and B site ions according to

\[H_{W-total} = H_{W-A}+H_{W-B} \label{3}\]

where

\[H_{W-A} = −\gamma_BM_B + γ_{AA}M_A \label{4a}\]

and

\[H_{W-B} = −\gamma_{AB}M_A + \gamma_{BB}M_B \label{4b}\]

where γ is the molecular field constant, which can be calculated using the Curie temperature T_c, magnetic moment µ_m, magnetization of each sublattice M, permeability of free space µ₀, and the Boltzmann's constant k_B:

\[\gamma = \dfrac{3k_BT_C}{\mu_m\mu_0M} \label{5}\]

Figure \(\PageIndex{4}\): (a) A tetrahedrally coordinated atom, and (b) an octahedrally coordinated atom. In both structures the black dot represents the transitional metal ion and the white circles represent oxygen ions in a ferrite.

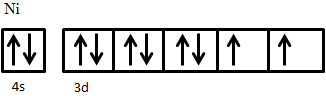
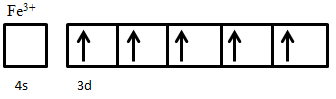
An example of ferrimagnetic material is nickel ferrite, NiO·Fe₂O₃. The Fe³⁺ ions are evenly distributed across both A and B sublattices, and thus their magnetic moments cancel out, while Ni²⁺ ions sit on B sites only. The electron configuration of nickel is 3d⁸4s² (Figure 5), from which two electrons are taken from 4s² to form Ni²⁺, giving an electron configuration of 3d^8. The electron spins of the ion are arranged according to Hund’s Rule. First, all five states are filled with one spin-up electron, leaving three electrons with down spin to be added. Adding these electrons in accordance to Hund’s rule results in two unpaired spin-up electrons. These two unpaired electrons produce a net magnetic moment on Ni²⁺ ions; since these all sit on the same sublattice they are parallel and produce a net magnetic moment in the crystal.

Figure \(\PageIndex{5}\): The electron configurations of \(Ni^{2+}\) and \(Fe^{3+}\)

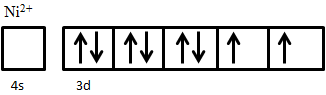
The arrangement of magnetic moments in the inverse spinel structure of a ferrite can be summarized as shown in Figure 6, metal cations on A site all have up-spin magnetic moments, and those on B sites all have down-spin moments. Five of the upwards pointing arrows are canceled by an arrow pointing down, leaving two remaining up arrows corresponding to a net magnetic moment of two.

Figure \(\PageIndex{6}\): Separation of magnetic moments into those on A sites and those on B sites: A site atoms all have spin-up unpaired electrons, and B site atoms all have spin-down unpaired electrons. The difference in the number of up and down arrows represents the net magnetic moment of the material.

Temperature Dependence

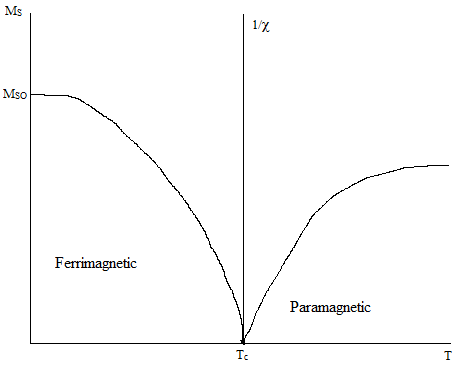
The temperature dependence of ferrimagnetic materials is similar to that of ferromagnetic materials. There is a Curie temperature at which the magnetic moments become randomized, causing ferrimagnetic materials to begin to behave paramagnetically. Before the Curie temperature, the saturation magnetization of a ferrimagnetic material decreases with increasing termpature until it vanishes completely at the Curie temperature, as illustrated in Figure 7. Above the Curie temperature, there is a 1/χ relationship with temperature, which also indicates a further decrease in magnetization.

Figure \(\PageIndex{7}\): The temperature dependence of magnetization in ferrimagnetic materials magnetization. In the region below the Curie temperature magnetization decreases as temperature increases. Above the Curie temperature, the ferrimagnetic material becomes paramagnetic.

Questions

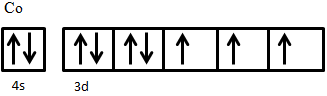
1. Show how the electrons fill the available 3d orbitals in Co³⁺ in its high-spin state.
2. What are the major similarities and differences between ferrimagnetism and antiferromagnetism?
3. What is the net magnetic moment in iron oxide FeO·Fe₂O₃?

Answers

1. 
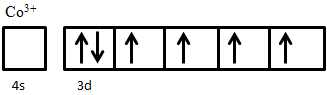
2. The major similarity between ferri- and antiferromagnetism is that they both experience superexchange behavior between ions that causes their magnetic moments to be antiparallel. The major difference between the two is that the net magnetic moment of the former is non-zero while in the latter it is zero. Antiferromagnetic materials thus do not exhibit spontaneous magnetization, while ferrimagnetic materials do.
3. Fe₂O₃ consists of Fe³⁺ and O^2- and has a net magnetic moment of zero. FeO consists of Fe²⁺ and O^2- ions; taking two electrons from the 4s orbital of Fe leaves Fe²⁺ with 6 electrons in its 3d orbital, and, according to Hund's rule, each Fe²⁺ ion will have 4 unpaired electrons (in its high-spin state).

References

1. Hummel, Rolf E. (2005). Electronic Properties of Materials, Fourth Edition. Chapter 15, pages 347-371. Springer
2. Spaldin, Nicola A. (2003) Magnetic Materials: Fundamentals and Applications, Second Edition. Chapter 9, pages 113-129. Cambridge University Press

Contributors and Attributions

• Alan Wu (University of California, Davis, Materials Science and Engineering)
• Template:ContribFisher