Diamagnetism
- Page ID
- 329
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
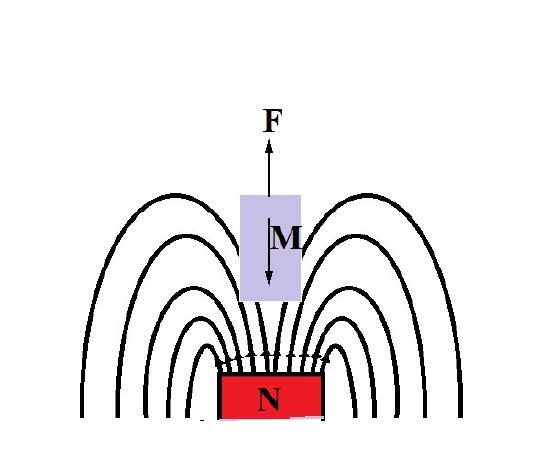
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The complete description of magnetic moment for a free atom incorporates the atomic angular moment, electron spin, and diamagnetic response. Essentially, diamagnetic behavior is the change in orbital angular momentum induced by an external magnetic field [1]. All materials exhibit a diamagnetic response, and it may be understood as the attempt to expel the applied magnetic field. The physical manifestation of these effects can be appreciated when a diamagnetic material is placed in the presence of a magnetic field and a force F repels the material, as in Figure \(\PageIndex{1}\). Typically, the diamagnetic susceptibility for a material is negative and on the order of 10-6, overwhelmed by other magnetic behavior such as in antiferromagnetism, if present [2].
Langevin Theory of Diamagnetism
Paul Langevin proposed a classical-based model of diamagnetism. Because this is a classical theory, it is an approximation, but its results give good agreement with experimental results [3]. Considering an electron moving in a loop, the induced magnetic moment is the product of the current in the loop and the area it encloses, or
\[\mu_m = IA \label{1}\]
Taking this as a model for a single orbiting electron, if exposed to the presence of an external magnetic field, the resulting change in the electron acceleration would induce a change in the magnetic moment. The acceleration can be quantified as
\[\dfrac{dv}{dt} = \dfrac{F}{m} = \dfrac{\mathcal{E}e}{m}\label{2} \]
Where the acceleration is equal to force per unit mass, which is the electric field strength times an electric charge per electron mass. Now apply Lenz's law and see that an emf is created to counteract the change in flux of the loop per unit length
\[\dfrac{\mathcal{E}e}{m} = \dfrac{-1}{2 \pi r} \dfrac{d}{dt} (\mu_0 H A) \label{3}\]
We can now find the acceleration by writing the magnetic moment as
\[\mu_m = e \dfrac{v}{2 \pi r} \pi r^2 \label{4}\]
and equating this to the previous acceleration equation giving the differential equation
\[dv = -\dfrac{e r \mu_0}{2 m} dH \label{5}\]
Which can be integrated to give:
\[\Delta v = -\dfrac{e r \mu_0 H}{2m} \label{6}\]
Substitute back into the magnetic moment equation and find
\[\Delta \mu_m = -\dfrac{e^2r^2 \mu_0 H}{4m} \label{7}\]
Taking the average of the change in magnetic moment (use polar coordinates, it is zero when the external magnetic field is parallel to the plane of the current loop) and the average distance (\(\bar{r}\)) from all electrons (\(Z\)) belonging to the atom
\[\overline{\Delta}\mu_m = -\dfrac{e^2 Z \bar{r}^2 \mu_0}{6 m} \label{8}\]
The average change in magnetic moment per atom becomes the diamagnetic susceptibility by simply taking into account the volume, \(V\), over which it acts.
\[\boxed{ \chi = -\dfrac{e^2 Z \bar{r}^2 \mu_0}{6 m V}} \label{9}\]
Diamagnetic Materials
The diamagnetic response of a material has a measurable contribution to the materials' magnetization only if there are no other magnetic effects present, such as Ferrimagnetism whose susceptibility is much larger in most cases [1]. For this reason, we classify only materials whose net magnetization is diamagnetic, as a diamagnet. This requires that compound to have empty or closed valence shell. The inert noble gases have filled valence shells and thus respond diamagnetically. Substances like silicon, germanium, most covalent solids and polymers also exhibit diamagnetic behavior [1].
Diamagnetism arises in metals when the paramagentic behavior is sufficiently small. For example, examine beryllium. It has no contribution from ferro, ferri, or antiferromagnetism, so we check its paramagnetic contribution. A single atom of beryllium has paired 1s and 2s electrons.
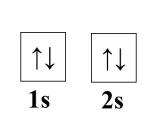
However, in a crystal lattice, the 2s electron populate the bottom of the empty 2p band because of band overlap (see: Band Theory of Metals and Insulators). This makes the density of states at the Fermi level very low, thus the paramagnetic susceptibility is much smaller than any diamagnetic contribution [3]. Landau set the framework for diamagnetic calculations of atoms in a lattice, see [4] for further reading.
Applications
Because diamagnetism is essentially the expelling of magnetic fields within a material, strong diamagnetic materials can be levitated, or if they are sufficiently strong and enough area, can levitate magnets. Figure \(\PageIndex{2}\) shows a levitating piece of graphite.

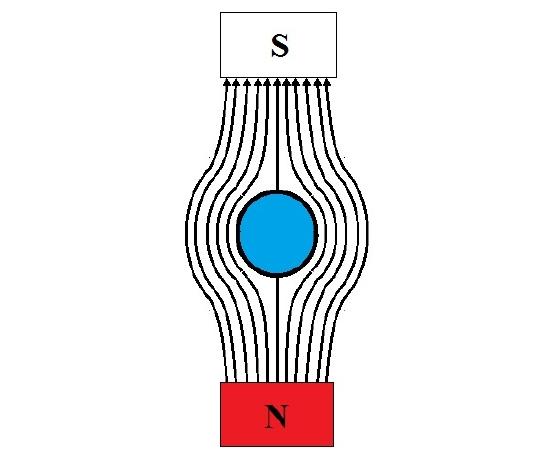
In the case of superconductors (Figure \(\PageIndex{3}\) ), the diamagnetic response leaves no internal magnetic field. These materials can be easily levitated in the presence of a strong permanent magnet as seen in Figure \(\PageIndex{2}\); this is called the Meissner effect. However, high temperature superconductors (~100 K [2]) are made from exotic materials with expensive processing routes and require cryogenic fluids to accomplish the superconducting state.
Questions
- Bismuth is heated from 298 K to 650 K, what is the change in diamagnetic susceptibility?
- Can you calculate the diamagnetic susceptibility of single crystal HCP titanium using the classical Langevin model? Explain why or why not..
- What is the ratio of magnetization to applied field for a YBCO crystal behaving as a superconductor at 77 K?
- Why would doping a piece of silicon change its bulk magnetic susceptibility? Now what happens if we vary the temperature?
Answers
- 0. From equation (1) we see that the diamagnetic susceptibility has no dependence on temperature, so heating a material will not change its diamagnetic susceptibility.
- No. The derivation of Langevin's susceptibility relies on the assumption that the material has a classically bound electron (rotating around an atom to create the magnetic moment), however, metals do not have localized electrons. Therefore, the substitutability cannot be determined using this theory.
- Because superconductors expel all of the magnetic field they are perfectly diamagnetic, or χ = M/H = 1, but the sense is opposite that of the applied field, so χ = -1.
- The susceptibility depends on the number of contributing electrons surrounding an atom, Z. Doping silicon introduces atoms that have different valencies and thus changes the overall susceptibility contribution of atoms in the material. By heating the material through different temperature regimes the electrons bound to their atoms can be freed, ionizing the donor atoms, such as in n-type silicon. The freed electrons populate the material at different temperatures (see: Extrinsic Semiconductors) making the susceptibility vary with temperature.
References
- N. A. Spaldin, Magnetic Materials: Fundamentals and Device Applications. Cambridge University Press, 2003
- S. O. Kasap, Principles of Electronic Materials and Devices. McGraw-Hill, 2006
- R. E. Hummel, Electronic Properties of Materials. Springer New York, 2013. p. 337-378
- B. M. Askerov, S. R. Figarova, M. M. Makhmudov, and V. R. Figarov, “Diamagnetism of an electron gas in superlattices,” Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, vol. 464, no. 2100, pp. 3213–3218, Dec. 2008.
Contributors and Attributions
- Lino Romero, Materials Science & Engineering - University of California, Davis

