6.2: Principles of Thermal Processing of Packaged Foods
- Page ID
- 46858
Ricardo Simpson
Departamento de Ingeniería Química y Ambiental, Universidad Técnica Federico Santa María, Valparaíso, Chile
Centro Regional de Estudios en Alimentos y Salud (CREAS) Conicyt-Regional GORE Valparaíso Project R17A10001, Curauma, Valparaíso, Chile
Helena Nuñez
Departamento de Ingeniería Química y Ambiental, Universidad Técnica Federico Santa Maria, Valparaíso, Chile
Cristian Ramírez
Departamento de Ingeniería Química y Ambiental, Universidad Técnica Federico Santa María, Valparaíso, Chile
Centro Regional de Estudios en Alimentos y Salud (CREAS) Conicyt-Regional GORE Valparaíso Project R17A10001, Curauma, Valparaíso, Chile
| Key Terms |
| Heat transfer | Bacterial inactivation | Food sterilization |
| Microorganism heat resistance | Decimal reduction time | Commercial sterilization |
Variables
Introduction
Thermal processing of foods, like cooking, involves heat and food. However, thermal processing is applied to ensure food safety and not necessarily to cook the food. Thermal processing as a means of preservation of uncooked food was invented in France in 1795 by Nicholas Appert, a chef who was determined to win the prize of 12,000 francs offered by Napoleon for a way to prevent military food supplies from spoiling. Appert worked with Peter Durand to preserve meats and vegetables encased in jars or tin cans under vacuum and sealed with pitch and, by 1804, opened his first vacuum-packing plant. This French military secret soon leaked out, but it took more than 50 years for Louis Pasteur to provide the explanation for the effectiveness of Appert’s method, when Pasteur was able to demonstrate that the growth of microorganisms was the cause of food spoilage.
The preservation for storage by thermal treatment and removal of atmosphere is known generically as canning, regardless of what container is used to store the food. The basic principles of canning have not changed dramatically since Appert and Durand developed the process: apply enough heat to food to destroy or inactivate microorganisms, then pack the food into sealed or “airtight” containers, ideally under vacuum. Canned foods have a shelf life of one to four years at ordinary temperatures, making them convenient, affordable, and easy to transport.
Outcomes
After reading this chapter, you should be able to:
- • Identify the role of heat transfer concepts in thermal processing of packaged foods
- • Describe the principles of commercial sterilization of foods
- • Describe the inactivation conditions needed for some example microorganisms important for food safety
- • Define some sterilization criteria for specific foods
- • Apply, in simple form, the main thermal food processing evaluation techniques
Concepts
The main concepts used in thermal processing of foods include: (a) heat transfer; (b) heat resistance of microorganisms of concern; and (c) bacterial inactivation.
Heat Transfer
The main heat transfer mechanisms involved in the thermal processing of packaged foods are convection and conduction. Heat transfer by convection occurs due to the motion and mixing of flows. The term natural convection refers to the case when motion and mixing of flow is caused by density differences in different locations due to temperature gradients. The term forced convection refers to the case when motion and mixing of flow is produced by an outside force, e.g., a fan. Heat transfer by conduction occurs when atoms and molecules collide, transferring kinetic energy. Conceptually, atoms are bonded to their neighbors, and if energy is supplied to one part of the solid, atoms will vibrate and transfer their energy to their neighbors and so on.
The main heat transfer mechanisms involved in the thermal processing of packaged foods are shown in Figure 6.2.1. Although the figure shows a cylindrical can (a cylinder of finite diameter and height), a similar situation will arise when processing other types of packaging such as glass containers, retortable pouches, and rigid and semi-rigid plastic containers. In general, independent of shape, food package sizes range from 0.1 L to 5 L (Holdsworth and Simpson, 2016).
The main mechanism of heat transfer from the heating medium (e.g., steam or hot water) to the container or packaging is convection. Then heat transfers by conduction through the wall of the container or package. Once inside the container, heat transfer through the covering liquid occurs by convection, and in solid foods mainly by conduction. In case of liquid foods, the main mechanism is convection.
The rate of heat transfer in packaged foods depends on process factors, product factors, and package types. Process factors include retort temperature profile, process time, heat transfer medium, and container agitation. Product factors include food composition, consistency, initial temperature, initial spore load, thermal diffusivity, and pH. Factors related to package type are container material, because the rate of heat transfer depends on thermal conductivity and thickness of the material, and container shape, because the surface area per unit volume plays a role in the heat penetration rate.

For liquid foods, the heating rate is determined not only by the thermal diffusivity α, but also by the viscosity. The thermal diffusivity is a material property that represents how fast the heat moves through the food and is determined as:
\[ a=K_{t}/(\rho\ C_{p}) \]
where α = thermal diffusivity (m2/s)
- Kt = thermal conductivity (W/m-K)
- ρ = density (kg/m3)
- Cp = specific heat (W/s-kg-K)
It is extremely difficult to develop a theoretical model for the prediction of a time-temperature history within the packaging material. Therefore, from a practical point of view, a satisfactory thermal process (i.e., time-temperature relationship) is usually determined using the slowest heating point, the cold spot, inside the container.
Heat Resistance of Microorganisms of Concern
The main objective in the design of a sterilization process for foods is the inactivation of the microorganisms that cause food poisoning and spoilage. In order to design a safe sterilization process, the appropriate operating conditions (time and temperature) must be determined to meet the pre-established sterilization criterion. To establish this criterion, it is necessary to know the heat resistance of the microorganisms (some examples are given in Table 6.2.1), the thermal properties of the food and packaging, and the shape and dimensions of the packaged food. From these, it is possible to determine the retort temperature and holding time (that is, the conditions for inactivation), how long it will take to reach that temperature (the come-up time), and how long it will take to cool to about 40°C (the cooling time) (Holdsworth and Simpson, 2016).
| Organism | Conditions for Inactivation |
|---|---|
|
Vegetative cells |
10 min at 80°C |
|
Yeast ascospores |
5 min at 60°C |
|
Fungi |
30–60 min at 88°C |
|
Thermophilic organisms: |
|
|
Bacillus stearothermophilus |
4 min at 121.1°C |
|
Clostridium thermosaccharolyticum |
3–4 min at 121.1°C |
|
Mesophilic organisms: |
|
|
Clostridium botulinum spores |
3 min at 121.1°C |
|
Clostridium botulinum toxins Types A & B |
0.1–1 min at 121.1°C |
|
Clostridium sporogenes |
1.5 min at 121.1°C |
|
Bacillus subtilis |
0.6 min at 121.1°C |
The pH of the food is extremely relevant to the selection of the sterilization process parameters, i.e., retort temperature and holding time, because microorganisms grow better in a less acid environment. That is why the standard commercial sterilization process is based on the most resistant microorganism (Clostridium botulinum) at the worst-case scenario conditions (higher pH) (Teixeira et al., 2006). The microorganism heat resistance is greater in low-acid products (pH ≥ 4.5–4.6). On the other hand, medium-acid to acidic foods require a much gentler heat treatment (lower temperature) to meet the sterilization criterion. Based on that, foods are classified into three groups:
- low-acid products: pH > 4.5–4.6 (e.g., seafood, meat, vegetables, dairy products);
- medium-acid products: 3.7 < pH < 4.6 (e.g., tomato paste);
- acidic products: pH < 3.7 (e.g., most fruits).
Bacterial Inactivation
Abundant scientific literature supports the application of first-order kinetics to quantify bacterial (spores) inactivation as (Esty and Meyer, 1922; Ball and Olson, 1957; Stumbo, 1973, Holdsworth and Simpson, 2016):
\[ (\dfrac{dN}{dt})_{I} = -kN \]
where \(N\) = viable bacterial (microbial) concentration (microorganisms/g) after process time t
- t = time
- I = inactivation
- k = bacterial inactivation rate constant (1/time)
Instead of k, food technologists have utilized the concept of decimal reduction time, D, defined as the time to reduce bacterial concentration by ten times. In other words, D is the required time at a specified temperature to inactivate 90% of the microorganism’s population. A mathematical expression that relates the rate constant, k, from Equation 6.2.2 to D is developed by separating variables and integrating the bacterial concentration from the initial concentration, N0, to N0/10 and from time 0 to D, therefore obtaining:
\[ k=\dfrac{ln\ 10}{D} = \dfrac{2.303}{D} \]
or
\[ D = \dfrac{ln\ 10}{k} = \dfrac{2.303}{k} \]
where k = reaction rate constant (1/min)
D = decimal reduction time (min)
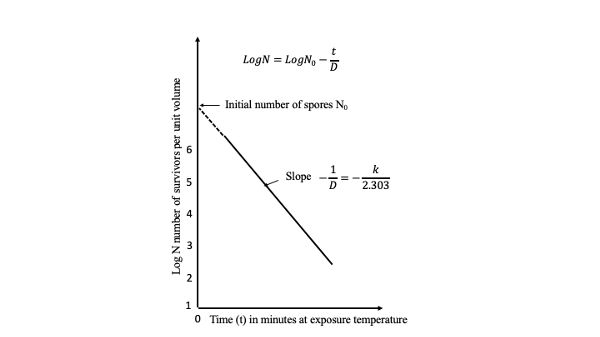
A plot of the log of the survivors (log N) against D is called a survivor curve (Figure 6.2.2). The slope of the line through one log cycle (decimal reduction) is −1/D and
\[ log\ N = log\ N_{0} - \dfrac{t}{D} \]
where N = number of survivors
N0 = N at time zero, the start of the process
Temperature Dependence of the Decimal Reduction Time, D
Every thermal process of a food product is a function of the thermal resistance of the microorganism in question. When the logarithm of the decimal reduction time, D, is plotted against temperature, a straight line results. This plot is called the thermal death time (TDT) curve (Figure 6.2.3). From such a plot, the thermal sensitivity of a microorganism, z, can be determined as the temperature change necessary to vary TDT by one log cycle.

Bigelow and co-workers (Bigelow and Esty, 1920; Bigelow, 1921) were the first to coin the term thermal death rate to relate the temperature dependence of D. Mathematically, the following expression has been used:
\[ log\ D = log\ D_{ref}-\dfrac{T-T_{ref}}{z} \]
or
\[ D = D_{ref}10^{\dfrac{T-T_{ref}}{z}} \]
where D = decimal reduction time at temperature T (min)
Dref = decimal reduction time at reference temperature Tref (min)
z = temperature change necessary to vary TDT by one log cycle (°C), e.g., normally z = 10°C for Clostridium botulinum
T = temperature (°C)
Tref = reference temperature (normally 121.1°C for sterilization)
The D value is directly related to the thermal resistance of a given microorganism. The more resistant the microorganism to the heat treatment, the higher the D value. On the other hand, the z value represents the temperature dependency but has no relation to the thermal resistance of the target microorganism. Then, the larger the z value the less sensitive the given microorganism is to temperature changes. D values are expressed as DT. For example, D140 means the time required to reduce the microbial population by one log cycle when the food is heated at 140°C.
Food Sterilization Criterion and Calculation
Sterilization means the complete destruction or inactivation of microorganisms. The food science and engineering community has accepted the utilization of a first-order kinetic for Clostridium botulinum inactivation (Equation 6.2.2). Again, this pathogen is the target microorganism in processes that use heat to sterilize foods. Theoretically, the inactivation time needed to fully inactivate Clostridium botulinum is infinite. According to Equations 6.2.2 and 6.2.3 and assuming a constant process temperature and that k is constant, the following expression is obtained:
\[ N_{f} = N_{0}e^{-kt} = N_{0}e^{-\dfrac{ln10}{D}t} \]
This equation shows that the final concentration of Clostridium botulinum (Nf) tends to zero when time (t) tends to infinity; therefore, it is not possible to reach a final concentration equal to zero for the target microorganism. Thus, it is necessary to define a sterilization criterion (or commercial sterilization criterion) to design a process that guarantees a safe product within a finite time.
The level of microbial inactivation, defined by the microbial lethality value or cumulative lethality, is the way in which the sterilization process is quantified. Specifically, the sterilizing value, denoted by F0, is the required time at 121.1°C to achieve 12 decimal reductions (12D). In other words, F0 is the time required to reduce the initial microorganism concentration from N0 to N0/1012 at the process temperature of 121.1°C.
The 12D sterilization criterion is an extreme process (i.e., overkill) designed to ensure no cells of C. botulinum remain in the food and, therefore, prevent illness or death. According to the FDA (1972), the minimum thermal treatment for a low-acid food should reach a minimum F0 value of 3 min (that is larger than 12D; D for C. botulinum at 121.1°C is 0.21 min, then 12 × 0.21 = 2.52 min, which is lower than 3 min). Thus, a thermal process for commercial sterilization of a food product should have an F0 value greater than 3 minutes.
The F0 attained for a food can be calculated easily when the temperature at the center of the food during the thermal processing is known by:
\[ F_{0}=\int^{t}_{0}10^{\dfrac{T-T_{ref}}{z}}dt \]
where F0 = cumulative lethality of the process from time 0 to the end of the process (t)
T = temperature measured at the food cold spot, which is the place in the food that heats last
Tref = temperature of microorganism reference; for sterilization of low-acid foods, Tref = 121.1°C for C. botulinum
z = temperature change necessary to reduce D value by ten times; in the case of sterilization of low-acid foods, z = 10°C for C. botulinum
t = process time to reach F0
Equation 6.2.9 can be calculated according to the general method proposed by Bigelow and co-workers 100 years ago (Bigelow et al., 1920; Simpson et al., 2003).
If the food is heated instantaneously to 121.1°C and maintained at this temperature for 3 min, then the F0 value for this process will be 3 min. From Equation 6.2.9,
\(F_{0}=\int^{t}_{0}10^{\dfrac{121.1-121.1}{10}}dt=\int^{t}_{0}10^{0}dt=\int^{3}_{0}1dt \)
Since the time interval is between 0 to 3 min, then the integral solution is 3 min or \(\int^{3}_{0}1dt\)= 3 – 0 = 3. However, in practice, due to the resistance of the food to the transfer of heat, the thermal sterilization process requires a longer time in order to get a F0 ≥ 3 min, because a significant part of the processing time is needed to raise the cold-spot temperature of the food and later to cool the food.
Applications
Commercial Sterilization Process
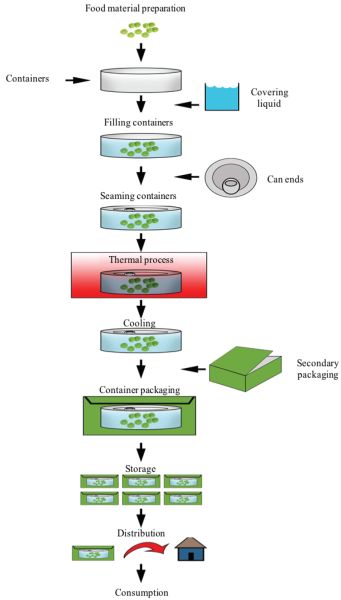
A general, simplified flow diagram for a typical commercial canning factory is presented in Figure 6.2.4.
Stage 1: Selecting and preparing the food as cleanly, rapidly, and precisely as possible. Foods that maintain their desirable color, flavor, and texture through commercial sterilization include broccoli, corn, spinach, peas, green beans, peaches, cherries, berries, sauces, purees, jams and jellies, fruit and vegetable juices, and some meats (Featherstone, 2015). The preparation must be performed with great care and with the least amount of damage and loss to minimize the monetary cost of the operation. If foods are not properly handled, the effectiveness of the sterilization treatment is compromised.
Stage 2: Packing the product in hermetically sealable containers (jars, cans, or pouches) and sealing under a vacuum to eliminate residual air. A less common approach is to sterilize the food first and then aseptically package it (aseptic processing and packaging of foods).
Stage 3: Stabilizing the food by sterilizing through rigorous thermal processing (i.e., high temperature to achieve the correct degree of sterilization or the target destruction of the microorganisms present in the food), followed by cooling of the product to a low temperature (about 40°C), at which enzymatic and chemical reactions begin to slow down.
Stage 4: Storing at a temperature below 35°C, the temperature below which food-spoilage organisms cannot grow.
Stage 5: Labeling, secondary packaging, distribution, marketing, and consumption. Although not part of the thermal process per se, this stage addresses the steps required for commercialization of the treated foods.
Stage 3, thermal processing, is the focus of this chapter. The aim of the thermal process is to inactivate, by the effect of heat, spores and microorganisms present in the unprocessed product. The thermal process is performed in vessels known as retorts or autoclaves to achieve the required high temperatures (usually above 100°C).
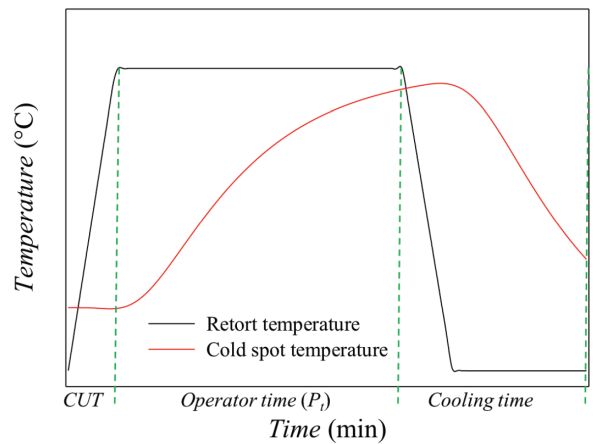
As depicted in Figure 6.2.5, a typical sterilization process has three main steps: come-up time, operator process time, and cooling. The first step, the come-up time (CUT), is the time required to reach the specified retort temperature (TRT), i.e., the target temperature in the retort. The second step is the holding time (Pt), also called operator process time, which is the amount of time that the retort temperature must be maintained to ensure the desired degree of lethality. This depends on the target microorganism or the expected microbiological contamination. The final step is the cooling, when the temperature of the product is decreased by introducing cold water into the retort. The purpose of cooling the food is to minimize the excessive (heat) processing of the food, and avoid the risk of thermophilic microorganism development. During the cooling cycle, it may be necessary to inject sterile air into the food packaging to avoid sudden internal pressure drops and prevent package deformation.
The concepts described in this chapter describe the key principles for applying a thermal process to packaged food to achieve the required lethality for food safety. These concepts can be used to design a thermal process to ensure adequate processing time and food safety while avoiding over processing the packaged food. This should ensure safe, tasty, and nutritious packaged foods.
Examples
Example \(\PageIndex{1}\)
Example 1: Calculation of microbial count after a given thermal process
Problem:
The D120°C value for a microorganism is 3 minutes. If the initial microbial contamination is 1012 cells per gram of product, how many microorganisms will remain in the sample after heat treatment at 120°C for 18 minutes?
Solution
Calculate the number of remaining cells using Equation 6.2.5 with N0 = 1012 cells/g, t = 18 minutes, and D120°C = 3 minutes.
From Equation 6.2.5,
\( log\ N_{(t)} =log\ N_{0}-\dfrac{t}{D} \)
\( log\ N_{(18)} =log\ 10^{12}\dfrac{\text{cells}}{g}-\dfrac{18\text{ min}}{3\text{ min}} \)
Solving for N(18) yields:
\( N_{(18)} =10^{6}\text{ cells/g} \)
Discussion:
Starting with a known microbial concentration (N0), the final concentration of a specific microorganism for a given thermal process at constant temperature can be calculated if the thermal resistance of the microorganism at a given temperature is known. In this case, D120°C = 3 min.
Example \(\PageIndex{2}\)
Example 2: Calculation of z value for a particular microorganism
Problem:
D of a given bacterium in milk at 65°C is 15 minutes. When a food sample that has 1010 cells of the bacterium per gram of food is heated for 10 minutes at 75°C, the number of survivors is 2.15 × 103 cells. Calculate z for this bacterium.
Solution
First, calculate D at the process temperature of 75°C, D75°C, using Equation 6.2.5. Then calculate z using Equation 6.2.6 with D65°C = 15 minutes, N0 = 1010 cells/g, and t = 10 minutes at T = 75°C.
\( log\ N_{(t)} = log\ N_{0} - \dfrac{t}{D} \) (Equation \(\PageIndex{5}\))
\( log\ 2.15\times10^{3} \text{ cells/g} = log\ 10^{10} \text{ cells/g}-\dfrac{10\text{ min}}{D_{75^\circ C}} \)
and D75°C = 1.5 min.
To calculate z, recall Equation 6.2.6:
\( log\ D = log\ D_{ref} - \dfrac{T-T_{ref}}{z} \)
Solving for z, Equation 6.2.6 can be expressed as:
\( z = \dfrac{\Delta T}{log(\dfrac{D_{1}}{D_{2}})} \)
with ∆T = (75 – 65)°C, D1 = D65°C and D2 = D75°C,
\( z = \dfrac{75-65}{log(\dfrac{15}{1.5})}=10 ^\circ C \)
Discussion:
As previously explained, the z value represents the change in process temperature required to reduce the D value of the target microorganism by ten times. In this case, the z value is 10°C and accordingly the D value was reduced 10 times, from 15 minutes to 1.5 minutes.
Example \(\PageIndex{3}\)
Example 3: Lethality of thermal processing of a can of tuna fish
Problem:
Table 6.2.2 presents the values of temperature measured in the retort (TRT) and the temperature measured at the cold spot of a can of tuna fish (Tcold spot) during a thermal process. The total process time was 63 min until the product was cold enough to be withdrawn from the retort.
- (a) Determine CUT (the time required to come up to TRT), operator process time Pt, and cooling time.
- (b) Determine the lethality value (F0) attained for the can of tuna fish.
| Time (min) | TRT (°C) | Tcold spot (°C) |
|---|---|---|
|
0.97 |
29.7 |
45.0 |
|
1.97 |
39.7 |
45.0 |
|
2.97 |
49.7 |
45.0 |
|
3.97 |
59.7 |
45.0 |
|
4.97 |
69.7 |
44.9 |
|
5.97 |
79.7 |
44.9 |
|
6.97 |
89.7 |
44.8 |
|
7.97 |
99.7 |
44.7 |
|
8.97 |
109.7 |
44.7 |
|
9.97 |
119.7 |
44.8 |
|
10.97 |
120.0 |
45.0 |
|
11.97 |
120.0 |
45.4 |
|
12.97 |
120.0 |
46.0 |
|
13.97 |
120.0 |
46.9 |
|
14.97 |
120.0 |
48.0 |
|
15.97 |
120.0 |
49.3 |
|
16.97 |
120.0 |
50.8 |
|
17.97 |
120.0 |
52.6 |
|
18.97 |
120.0 |
54.4 |
|
19.97 |
120.0 |
56.4 |
|
20.97 |
120.0 |
58.5 |
|
21.97 |
120.0 |
60.6 |
|
22.97 |
120.0 |
62.8 |
|
23.97 |
120.0 |
65.0 |
|
24.97 |
120.0 |
67.1 |
|
25.97 |
120.0 |
69.3 |
|
26.97 |
120.0 |
71.4 |
|
27.97 |
120.0 |
73.5 |
|
28.97 |
120.0 |
75.5 |
|
29.97 |
120.0 |
77.5 |
|
30.97 |
120.0 |
79.4 |
|
31.97 |
120.0 |
81.2 |
|
32.97 |
120.0 |
83.0 |
|
33.97 |
120.0 |
84.7 |
|
34.97 |
120.0 |
86.3 |
|
35.97 |
120.0 |
87.9 |
|
36.97 |
120.0 |
89.4 |
|
37.97 |
120.0 |
90.8 |
|
38.97 |
120.0 |
92.2 |
|
39.97 |
120.0 |
93.6 |
|
40.97 |
120.0 |
94.8 |
|
41.97 |
120.0 |
96.0 |
|
42.97 |
120.0 |
97.2 |
|
43.97 |
120.0 |
98.3 |
|
44.97 |
120.0 |
99.3 |
|
45.97 |
120.0 |
100.3 |
|
46.97 |
120.0 |
101.3 |
|
47.97 |
120.0 |
102.2 |
|
48.97 |
120.0 |
103.0 |
|
49.97 |
120.0 |
103.9 |
|
50.97 |
120.0 |
104.7 |
|
51.97 |
120.0 |
105.4 |
|
52.97 |
120.0 |
106.1 |
|
53.97 |
120.0 |
106.8 |
|
54.97 |
120.0 |
107.4 |
|
55.97 |
120.0 |
108.0 |
|
56.97 |
120.0 |
108.6 |
|
57.97 |
120.0 |
109.2 |
|
58.97 |
120.0 |
109.7 |
|
59.97 |
120.0 |
110.2 |
|
60.97 |
120.0 |
110.7 |
|
61.97 |
120.0 |
111.1 |
|
62.97 |
120.0 |
111.6 |
|
63.97 |
120.0 |
112.0 |
|
64.97 |
120.0 |
112.4 |
|
65.97 |
120.0 |
112.8 |
|
66.97 |
120.0 |
113.1 |
|
67.97 |
120.0 |
113.4 |
|
68.97 |
120.0 |
113.8 |
|
69.97 |
120.0 |
114.1 |
|
70.97 |
120.0 |
114.4 |
|
71.97 |
120.0 |
114.6 |
|
72.97 |
120.0 |
114.9 |
|
73.97 |
120.0 |
115.2 |
|
74.97 |
120.0 |
115.4 |
|
76 |
25.0 |
115.6 |
|
77 |
25.0 |
115.8 |
|
78 |
25.0 |
116.0 |
|
79 |
25.0 |
116.2 |
|
80 |
25.0 |
116.2 |
|
81 |
25.0 |
116.0 |
|
82 |
25.0 |
115.5 |
|
83 |
25.0 |
114.6 |
|
84 |
25.0 |
113.4 |
|
85 |
25.0 |
111.8 |
|
86 |
25.0 |
110.0 |
|
87 |
25.0 |
107.9 |
|
88 |
25.0 |
105.6 |
|
89 |
25.0 |
103.1 |
|
90 |
25.0 |
100.6 |
|
91 |
25.0 |
97.9 |
|
92 |
25.0 |
95.3 |
|
93 |
25.0 |
92.6 |
|
94 |
25.0 |
89.9 |
|
95 |
25.0 |
87.3 |
|
96 |
25.0 |
84.7 |
|
97 |
25.0 |
82.1 |
|
98 |
25.0 |
79.6 |
|
99 |
25.0 |
77.2 |
|
100 |
25.0 |
74.9 |
|
101 |
25.0 |
72.6 |
|
102 |
25.0 |
70.5 |
|
103 |
25.0 |
68.4 |
|
104 |
25.0 |
66.3 |
|
105 |
25.0 |
64.4 |
|
106 |
25.0 |
62.6 |
|
107 |
25.0 |
60.8 |
|
108 |
25 |
59.08 |
|
109 |
25 |
57.46 |
|
110 |
25 |
55.91 |
|
111 |
25 |
54.43 |
|
112 |
25 |
53.01 |
|
113 |
25 |
51.67 |
|
114 |
25 |
50.38 |
|
115 |
25 |
49.15 |
|
116 |
25 |
47.99 |
|
117 |
25 |
46.87 |
|
118 |
25 |
45.81 |
|
119 |
25 |
44.8 |
|
120 |
25 |
43.84 |
|
121 |
25 |
42.92 |
|
122 |
25 |
42.05 |
|
123 |
25 |
41.22 |
|
124 |
25 |
40.43 |
Solution
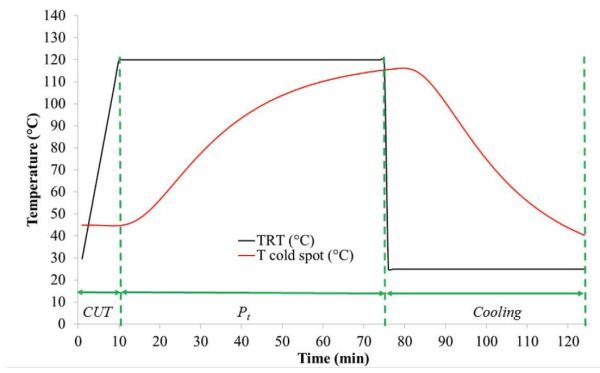
- (a) To determine CUT and Pt, plot TRT and Tcold spot against time, which produces the thermal profiles in Figure 6.2.6.
Figure 6.2.6 shows that the CUT is approximately 10 min and Pt, during which process temperature is maintained constant at 120°C, is approximately 64 min.
- (b) The lethality value, F0, can be obtained through numerical integration of Equation 6.2.9 using the trapezoidal rule (Patashnik, 1953). The calculations can be completed as follows or using software such as Excel.
As presented in Table 6.2.3, for each time, we can evaluate Equation 6.2.9:
-
\( F_{0}=\int^{t}_{0}10^{\dfrac{T-121.1}{10}}dt \) (Equation \(\PageIndex{9}\))
where T = Tcold spot and Tref and z-value for Clostridium botulinum are 121.1°C and 10°C, respectively.
- Given that F0 corresponds to the integral of 10[(Tcold spot −Tref)/z], this can be solved numerically by the trapezoidal rule method, i.e., by determining the area under the curve by dividing the area into trapezoids, computing the area of each trapezoid, and summing all trapezoidal areas to yield F0. (More details about the trapezoidal rule are included in the appendix.) The calculations are summarized in Table 6.2.3. In this particular case, F0 was about 6.07 min. The change of F0 along the thermal process is shown as the blue line in Figure 6.2.7.
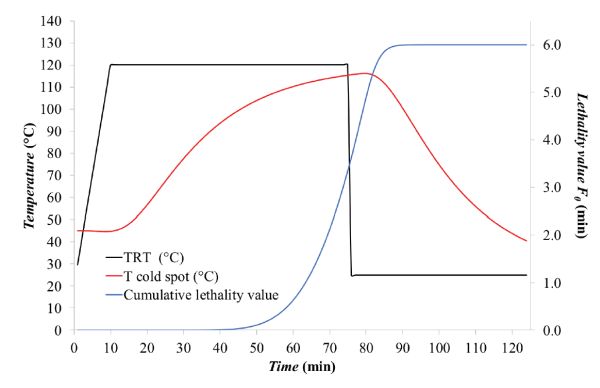
| Time (min) | TRT (°C) | Tcold spot (°C) | (Tcold spot − Tref)/z | 10[(Tcold spot −Tref)/z] | Trapezoidal Area | Sum of Areas |
|---|---|---|---|---|---|---|
|
0.97 |
29.67 |
45 |
−7.6 |
0.000 |
0.000 |
0.000 |
|
1.97 |
39.67 |
45 |
−7.6 |
0.000 |
0.000 |
0.000 |
|
2.97 |
49.67 |
44.99 |
−7.6 |
0.000 |
0.000 |
0.000 |
|
3.97 |
59.67 |
44.97 |
−7.6 |
0.000 |
0.000 |
0.000 |
|
4.97 |
69.67 |
44.93 |
−7.6 |
0.000 |
0.000 |
0.000 |
|
5.97 |
79.67 |
44.85 |
−7.6 |
0.000 |
0.000 |
0.000 |
|
6.97 |
89.67 |
44.76 |
−7.6 |
0.000 |
0.000 |
0.000 |
|
7.97 |
99.67 |
44.69 |
−7.6 |
0.000 |
0.000 |
0.000 |
|
8.97 |
109.67 |
44.68 |
−7.6 |
0.000 |
0.000 |
0.000 |
|
9.97 |
119.67 |
44.77 |
−7.6 |
0.000 |
0.000 |
0.000 |
|
10.97 |
120 |
45 |
−7.6 |
0.000 |
0.000 |
0.000 |
|
11.97 |
120 |
45.41 |
−7.6 |
0.000 |
0.000 |
0.000 |
|
12.97 |
120 |
46.03 |
−7.5 |
0.000 |
0.000 |
0.000 |
|
13.97 |
120 |
46.88 |
−7.4 |
0.000 |
0.000 |
0.000 |
|
14.97 |
120 |
47.97 |
−7.3 |
0.000 |
0.000 |
0.000 |
|
15.97 |
120 |
49.29 |
−7.2 |
0.000 |
0.000 |
0.000 |
|
16.97 |
120 |
50.83 |
−7.0 |
0.000 |
0.000 |
0.000 |
|
17.97 |
120 |
52.55 |
−6.9 |
0.000 |
0.000 |
0.000 |
|
18.97 |
120 |
54.42 |
−6.7 |
0.000 |
0.000 |
0.000 |
|
19.97 |
120 |
56.41 |
−6.5 |
0.000 |
0.000 |
0.000 |
|
20.97 |
120 |
58.49 |
−6.3 |
0.000 |
0.000 |
0.000 |
|
21.97 |
120 |
60.63 |
−6.0 |
0.000 |
0.000 |
0.000 |
|
22.97 |
120 |
62.79 |
−5.8 |
0.000 |
0.000 |
0.000 |
|
23.97 |
120 |
64.97 |
−5.6 |
0.000 |
0.000 |
0.000 |
|
24.97 |
120 |
67.14 |
−5.4 |
0.000 |
0.000 |
0.000 |
|
25.97 |
120 |
69.29 |
−5.2 |
0.000 |
0.000 |
0.000 |
|
26.97 |
120 |
71.41 |
−5.0 |
0.000 |
0.000 |
0.000 |
|
27.97 |
120 |
73.48 |
−4.8 |
0.000 |
0.000 |
0.000 |
|
28.97 |
120 |
75.5 |
−4.6 |
0.000 |
0.000 |
0.000 |
|
29.97 |
120 |
77.46 |
−4.4 |
0.000 |
0.000 |
0.000 |
|
30.97 |
120 |
79.36 |
−4.2 |
0.000 |
0.000 |
0.000 |
|
31.97 |
120 |
81.2 |
−4.0 |
0.000 |
0.000 |
0.000 |
|
32.97 |
120 |
82.97 |
−3.8 |
0.000 |
0.000 |
0.001 |
|
33.97 |
120 |
84.67 |
−3.6 |
0.000 |
0.000 |
0.001 |
|
34.97 |
120 |
86.31 |
−3.5 |
0.000 |
0.000 |
0.001 |
|
35.97 |
120 |
87.89 |
−3.3 |
0.000 |
0.001 |
0.002 |
|
36.97 |
120 |
89.4 |
−3.2 |
0.001 |
0.001 |
0.003 |
|
37.97 |
120 |
90.84 |
−3.0 |
0.001 |
0.001 |
0.004 |
|
38.97 |
120 |
92.22 |
−2.9 |
0.001 |
0.002 |
0.005 |
|
39.97 |
120 |
93.55 |
−2.8 |
0.002 |
0.002 |
0.007 |
|
40.97 |
120 |
94.81 |
−2.6 |
0.002 |
0.003 |
0.010 |
|
41.97 |
120 |
96.02 |
−2.5 |
0.003 |
0.004 |
0.014 |
|
42.97 |
120 |
97.17 |
−2.4 |
0.004 |
0.005 |
0.018 |
|
43.97 |
120 |
98.27 |
−2.3 |
0.005 |
0.006 |
0.024 |
|
44.97 |
120 |
99.31 |
−2.2 |
0.007 |
0.007 |
0.032 |
|
45.97 |
120 |
100.31 |
−2.1 |
0.008 |
0.009 |
0.041 |
|
46.97 |
120 |
101.27 |
−2.0 |
0.010 |
0.012 |
0.053 |
|
47.97 |
120 |
102.17 |
−1.9 |
0.013 |
0.014 |
0.067 |
|
48.97 |
120 |
103.04 |
−1.8 |
0.016 |
0.017 |
0.084 |
|
49.97 |
120 |
103.86 |
−1.7 |
0.019 |
0.021 |
0.105 |
|
50.97 |
120 |
104.65 |
−1.6 |
0.023 |
0.025 |
0.130 |
|
51.97 |
120 |
105.39 |
−1.6 |
0.027 |
0.029 |
0.159 |
|
52.97 |
120 |
106.1 |
−1.5 |
0.032 |
0.034 |
0.193 |
|
53.97 |
120 |
106.78 |
−1.4 |
0.037 |
0.040 |
0.233 |
|
54.97 |
120 |
107.42 |
−1.4 |
0.043 |
0.046 |
0.279 |
|
55.97 |
120 |
108.04 |
−1.3 |
0.049 |
0.053 |
0.332 |
|
56.97 |
120 |
108.62 |
−1.2 |
0.056 |
0.060 |
0.393 |
|
57.97 |
120 |
109.18 |
−1.2 |
0.064 |
0.068 |
0.461 |
|
58.97 |
120 |
109.7 |
−1.1 |
0.072 |
0.077 |
0.538 |
|
59.97 |
120 |
110.21 |
−1.1 |
0.081 |
0.086 |
0.624 |
|
60.97 |
120 |
110.69 |
−1.0 |
0.091 |
0.096 |
0.720 |
|
61.97 |
120 |
111.14 |
−1.0 |
0.101 |
0.106 |
0.826 |
|
62.97 |
120 |
111.57 |
−1.0 |
0.111 |
0.117 |
0.943 |
|
63.97 |
120 |
111.99 |
−0.9 |
0.123 |
0.129 |
1.072 |
|
64.97 |
120 |
112.38 |
−0.9 |
0.134 |
0.140 |
1.212 |
|
65.97 |
120 |
112.75 |
−0.8 |
0.146 |
0.153 |
1.365 |
|
66.97 |
120 |
113.11 |
−0.8 |
0.159 |
0.165 |
1.530 |
|
67.97 |
120 |
113.44 |
−0.8 |
0.171 |
0.178 |
1.708 |
|
68.97 |
120 |
113.76 |
−0.7 |
0.185 |
0.191 |
1.899 |
|
69.97 |
120 |
114.07 |
−0.7 |
0.198 |
0.205 |
2.104 |
|
70.97 |
120 |
114.36 |
−0.7 |
0.212 |
0.219 |
2.323 |
|
71.97 |
120 |
114.63 |
−0.6 |
0.225 |
0.233 |
2.555 |
|
72.97 |
120 |
114.9 |
−0.6 |
0.240 |
0.247 |
2.802 |
|
73.97 |
120 |
115.15 |
−0.6 |
0.254 |
0.261 |
3.063 |
|
74.97 |
120 |
115.38 |
−0.6 |
0.268 |
0.275 |
3.338 |
|
76 |
25 |
115.61 |
−0.5 |
0.282 |
0.290 |
3.628 |
|
77 |
25 |
115.83 |
−0.5 |
0.297 |
0.304 |
3.932 |
|
78 |
25 |
116.02 |
−0.5 |
0.310 |
0.316 |
4.248 |
|
79 |
25 |
116.17 |
−0.5 |
0.321 |
0.322 |
4.570 |
|
80 |
25 |
116.19 |
−0.5 |
0.323 |
0.315 |
4.885 |
|
81 |
25 |
115.97 |
−0.5 |
0.307 |
0.290 |
5.175 |
|
82 |
25 |
115.45 |
−0.6 |
0.272 |
0.248 |
5.422 |
|
83 |
25 |
114.58 |
−0.7 |
0.223 |
0.196 |
5.618 |
|
84 |
25 |
113.36 |
−0.8 |
0.168 |
0.143 |
5.761 |
|
85 |
25 |
111.81 |
−0.9 |
0.118 |
0.097 |
5.858 |
|
86 |
25 |
109.96 |
−1.1 |
0.077 |
0.062 |
5.920 |
|
87 |
25 |
107.87 |
−1.3 |
0.048 |
0.038 |
5.958 |
|
88 |
25 |
105.57 |
−1.6 |
0.028 |
0.022 |
5.980 |
|
89 |
25 |
103.12 |
−1.8 |
0.016 |
0.012 |
5.992 |
|
90 |
25 |
100.57 |
−2.1 |
0.009 |
0.007 |
5.999 |
|
91 |
25 |
97.94 |
−2.3 |
0.005 |
0.004 |
6.003 |
|
92 |
25 |
95.26 |
−2.6 |
0.003 |
0.002 |
6.005 |
|
93 |
25 |
92.58 |
−2.9 |
0.001 |
0.001 |
6.006 |
|
94 |
25 |
89.91 |
−3.1 |
0.001 |
0.001 |
6.007 |
|
95 |
25 |
87.26 |
−3.4 |
0.000 |
0.000 |
6.007 |
|
96 |
25 |
84.66 |
−3.6 |
0.000 |
0.000 |
6.007 |
|
97 |
25 |
82.11 |
−3.9 |
0.000 |
0.000 |
6.007 |
|
98 |
25 |
79.63 |
−4.1 |
0.000 |
0.000 |
6.007 |
|
99 |
25 |
77.22 |
−4.4 |
0.000 |
0.000 |
6.007 |
|
100 |
25 |
74.88 |
−4.6 |
0.000 |
0.000 |
6.007 |
|
101 |
25 |
72.62 |
−4.8 |
0.000 |
0.000 |
6.007 |
|
102 |
25 |
70.45 |
−5.1 |
0.000 |
0.000 |
6.007 |
|
103 |
25 |
68.35 |
−5.3 |
0.000 |
0.000 |
6.007 |
|
104 |
25 |
66.34 |
−5.5 |
0.000 |
0.000 |
6.007 |
|
105 |
25 |
64.41 |
−5.7 |
0.000 |
0.000 |
6.007 |
|
106 |
25 |
62.55 |
−5.9 |
0.000 |
0.000 |
6.007 |
|
107 |
25 |
60.78 |
−6.0 |
0.000 |
0.000 |
6.007 |
|
108 |
25 |
59.08 |
−6.2 |
0.000 |
0.000 |
6.007 |
|
109 |
25 |
57.46 |
−6.4 |
0.000 |
0.000 |
6.007 |
|
110 |
25 |
55.91 |
−6.5 |
0.000 |
0.000 |
6.007 |
|
111 |
25 |
54.43 |
−6.7 |
0.000 |
0.000 |
6.007 |
|
112 |
25 |
53.01 |
−6.8 |
0.000 |
0.000 |
6.007 |
|
113 |
25 |
51.67 |
−6.9 |
0.000 |
0.000 |
6.007 |
|
114 |
25 |
50.38 |
−7.1 |
0.000 |
0.000 |
6.007 |
|
115 |
25 |
49.15 |
−7.2 |
0.000 |
0.000 |
6.007 |
|
116 |
25 |
47.99 |
−7.3 |
0.000 |
0.000 |
6.007 |
|
117 |
25 |
46.87 |
−7.4 |
0.000 |
0.000 |
6.007 |
|
118 |
25 |
45.81 |
−7.5 |
0.000 |
0.000 |
6.007 |
|
119 |
25 |
44.8 |
−7.6 |
0.000 |
0.000 |
6.007 |
|
120 |
25 |
43.84 |
−7.7 |
0.000 |
0.000 |
6.007 |
|
121 |
25 |
42.92 |
−7.8 |
0.000 |
0.000 |
6.007 |
|
122 |
25 |
42.05 |
−7.9 |
0.000 |
0.000 |
6.007 |
|
123 |
25 |
41.22 |
−8.0 |
0.000 |
0.000 |
6.007 |
|
124 |
25 |
40.43 |
−8.1 |
0.000 |
0.000 |
6.007 |
Discussion:
The cumulative lethality, F0, was about 6.01 min, meaning that the process is safe according to FDA requirements, i.e., F0 ≥ 3 min (see the Food Sterilization Criterion and Calculation section above).
Example \(\PageIndex{4}\)
Example 4: Lethality of thermal processing of a can of mussels
Problem:
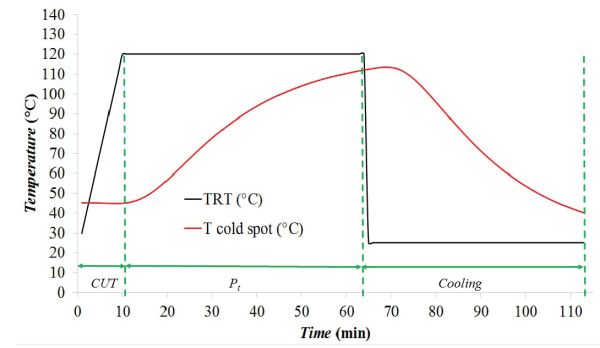
Temperatures measured in the retort and the temperature measured at the cold spot of a can of mussels during a thermal process performed at 120°C were recorded. The total process time was 113 min until the product was cold enough to be withdrawn from the retort. The measured thermal profiles (TRT and Tcold spot) were plotted, as was done in Example 6.2.3. The resulting plot (Figure 6.2.8) shows that CUT was approximately 10 min and Pt was approximately 53 min. The lethality value, F0, was obtained through numerical integration of Equation 6.2.9. In this case, F0 attained in the mussels can with a processing temperature of 120 °C was 2.508 min. The evolution of F0 along the thermal process is shown in Figure 6.2.9 as the blue line.
Discussion:
The cumulative lethality, F0, attained along the thermal process was 2.5 min, meaning that the process is not safe according to FDA requirements (F0 ≥ 3 min). Thus, the thermal processing time of canning process of mussels must be extended in order to reach the safety value recommended by the FDA.
Example \(\PageIndex{5}\)
Example 5: Processing time at different retort temperatures
Problem:
Determine the required processing time to get a lethality of 6 min (F0 = 6 min) when the retort temperature is (a) 120°C and considered equal to the cold spot temperature, (b) 110°C, and (c) 130°C.
Solution
The F0 is typically set for the 12D value to give a 12 log reduction of heat-resistant species of mesophilic spores (typically taken as C. botulinum). The Tref = 121.1°C and z = 10°C. Therefore, Equation 6.2.9 can be used directly by replacing T by the retort temperature, given that cold spot temperature can be assumed equal to retort temperature:
\( F_{0} = \int^{t}_{0}10^{\dfrac{T-121.1}{z}}dt \) (Equation \(\PageIndex{9}\))
\( 6 = \int^{t}_{0}10^{\dfrac{120-121.1}{10}}dt \)
\( t = \dfrac{6}{10^{\dfrac{120-121.1}{10}}} \)
Solving the integral yields a processing time, t, of 7.7 min.
- (b) When the temperature of the retort is reduced to 110°C, the lethality must be maintained at 6 min. Solving Equation 6.2.9:
\( 6 = \int^{t}_{0} 10^{\dfrac{110-121.1}{10}} dt \)
- gives the required processing time t of 77.2 min.
- (c) When the temperature of the retort is increased to 130°C, and maintaining the F0 = 6 min, the processing time is reduced to 0.77 min
\( 6 = \int^{t}_{0} 10^{\dfrac{130-121.1}{10}} dt \)
Discussion:
The results showed that as the temperature in the food increased in 10°C increments, the processing time was reduced by one decimal reduction. This variation is due to a z value of 10°C.
Appendix: The Trapezoidal Rule
A trapezoid is a four-sided region with two opposite sides parallel (Figure 6.2.10). The area of a trapezoid is the average length of the two parallel sides multiplied by the distance between the two sides. In Figure 6.2.11, the area (A) under function f(x) between points x0 and xn is given by:

\[ A=\int^{b}_{a} f(x)dx \]
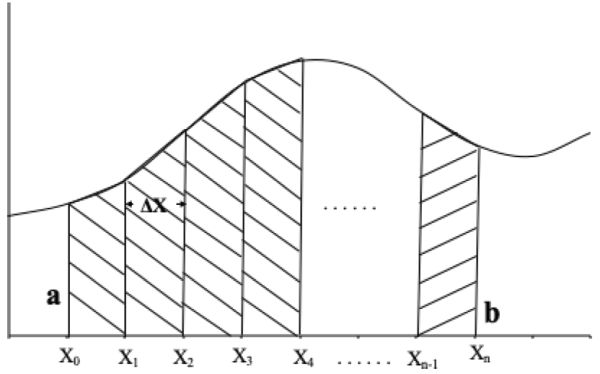
An approximation of the area A is the sum of the areas of the individual trapezoids (T), where T can be calculated using Equation 6.2.11:
\[ T=\dfrac{1}{2}\Delta x_{1}[f(x_{0})+f(x_{1})]+\dfrac{1}{2}\Delta x_{2}[f(x_{1})+f(x_{2})]+…+\dfrac{1}{2}\Delta x_{n}[f(x_{n-1})+f(x_{n})] \]
where \(\Delta x_{i}=x_{i}-x_{i-1}\), for i = 1, 2, 3, . . . , n
In the particular case where ∆x1 = ∆x2 = ∆x3 = . . . = ∆xn = ∆x, Equation 6.2.11 can be expressed as:
\[ T=\Delta x[\dfrac{f(x_{0})}{2} + f(x_{1})+ f(x_{2})+ f(x_{3})+…+\dfrac{f(x_{n})}{2} \]
or, in the following reduced form:
\[ T=\Delta x[\dfrac{f(x_{0})}{2} +\sum^{n-1}_{i=1}f(x_{i})+\dfrac{f(x_{n})}{2} \]
Finally, to estimate area A under the trapezoidal rule,
\[ A=\int^{x_{n}}_{x_{0}}f(x)dx\cong\dfrac{1}{2}\Delta x_{1}[f(x_{0})+f(x_{1})]+\dfrac{1}{2}\Delta x_{2}[f(x_{1})+f(x_{2})]+…+\dfrac{1}{2}\Delta x_{n}[f(x_{n-1})+f(x_{n})] \]
When all intervals are of the same size (∆x1 = ∆x2 = ∆x3 = . . . = ∆xn = ∆x), the following expression can be applied:
\[ A=\int^{x_{n}}_{x_{0}}f(x)dx\cong\Delta x(\dfrac{f(x_{0})}{2} +\sum^{n-1}_{i=1}f(x_{i})+\dfrac{f(x_{n})}{2}) =\dfrac{1}{2}\Delta x(f(x_{0}) +2\sum^{n-1}_{i=1}f(x_{i})+f(x_{n})) \]
Example \(\PageIndex{6}\)
Example
Problem:
Using the heat penetration data at the cold spot of a canned food in Table 6.2.4, calculate the cumulative lethality, F0, in the range of 23 to 27 min using the trapezoidal rule.
Table \(\PageIndex{4}\): Heat penetration data at the slowest heating point.
| Time (min) | Temperature (C) |
|---|---|
|
. . . |
. . . |
|
23 |
118.5 |
|
24 |
118.7 |
|
25 |
118.9 |
|
26 |
119.1 |
|
27 |
119.3 |
|
. . . |
. . . |
Solution
From Equation 6.2.9,
\( F_{0}=\int^{27}_{23}10^{\dfrac{T-121.1}{10}}dt \)
Applying the trapezoidal rule and considering that all time steps are equal (∆t = 1 min), calculate F0 using Equation 6.2.15,
\( F_{0}=\int^{27}_{23}10^{\dfrac{T-121.1}{10}}dt \cong \dfrac{1}{2}[f(23)+2f(24)+2f(25)+2f(26)+f(27)] \)
where ∆t = 1 (1 min interval), and:
\( f(23)=10^{\dfrac{118.5-121.1}{10}} = 0.549541 \)
\( f(24)=10^{\dfrac{118.7-121.1}{10}} = 0.57544 \)
\( f(25)=10^{\dfrac{118.9-121.1}{10}} = 0.6025596 \)
\( f(26)=10^{\dfrac{119.1-121.1}{10}} = 0.63095734 \)
\( f(27)=10^{\dfrac{119.3-121.1}{10}} = 0.66069345 \)
Replacing into equation (6.2.15):
\( F_{0}=\int^{27}_{23}10^{\dfrac{T-121.1}{10}}dt \cong \dfrac{1}{2}(0.549541+2\times0.57544+2\times0.6025596+2\times 0.63095734+0.66069345) \)
Therefore, F0 ~ 2.41407394 ~ 2.41 min.
Discussion:
The applied process to sterilize the target food is not safe since F0 < 3 minutes.
Image Credits
Figure 1. Simpson, R. (CC By 4.0). (2020). Main heat transfer mechanisms involved in the thermal processing of packaged foods. Retrieved from onlinelibrary.wiley.com
Figure 2. Holdsworth, S. Donald-Simpson, R. (CC By 4.0). (2020). Semilogarithmic survivor curve. Retrieved from https://www.springer.com/la/book/9783319249025
Figure 3. Holdsworth, S. Donald-Simpson, R. (CC By 4.0). (2020). Thermal death time (TDT) curve. Retrieved from https://www.springer.com/la/book/9783319249025.
Figure 4. Simpson, R. (CC By 4.0). (2020). Stages of a typical food commercial canning factory.
Figure 5. Ramírez, C. (CC By 4.0). (2020). Temperature profiles for a typical thermal process, where CUT is come-up time and Pt is operator time.
Figure 6. Ramírez, C. (CC By 4.0). (2020). Temperature profile of thermal processing data in table 2.
Figure 7. Ramírez, C. (CC By 4.0). (2020). Thermal process temperature profiles including the cumulative lethality value (F at any time t).
Figure 8. Ramírez, C. (CC By 4.0). (2020). Temperature profile of thermal processing data (Table 4).
Figure 9. Ramírez, C. (CC By 4.0). (2020). Thermal process temperature profiles including the cumulative lethality value (F at any time t).
Figure 10. Simpson, R. (CC By 4.0). (2020). Example of a trapezoid.
Figure 11. Simpson, R. (CC By 4.0). (2020). Curve divided into n equal parts each of length ΔX.
References
Ball, C. O., & Olson, F. C. (1957). Sterilization in food technology—Theory, practice and calculations. New York, NY: McGraw-Hill.
Bigelow, W. D. (1921). The logarithmic nature of thermal death time curves. J. Infectious Dis., 29(5), 528-536. https://doi.org/10.1093/infdis/29.5.528.
Bigelow, W. D., & Esty, J. R. (1920). The thermal death point in relation to time of typical thermophilic organisms. J. Infectious Dis., 27(6), 602-617. doi.org/10.1093/infdis/27.6.602.
Bigelow, W. D., Bohart, G. S., Richardson, A. C., & Ball, C. O. (1920). Heat penetration in processing canned foods. Bull. No. 16. Washington, DC: Research Laboratory, National Canners Association.
Esty, J. R., & Meyer, K. F. (1922). The heat resistance of the spores of B. botulinus and allied anaerobes. J. Infectious Dis., 31(6), 650-663. https://doi.org/10.1093/infdis/31.6.650.
FDA. (1972). Sterilizing symbols. Low acid canned foods. Inspection technical guide. Ch. 7. ORO/ETSB (HFC-133). Washington, DC: FDA.
Featherstone, S. (2015). 7: Retortable flexible containers for food packaging. In A complete course in canning and related processes (14th ed.). Vol. 2: Microbiology, packaging, HACCP and ingredients (pp. 137-146). Sawston, Cambridge, U.K.: Woodhead Publ. https://doi.org/10.1016/B978-0-85709-678-4.00007-5.
Holdsworth, S. D., & Simpson, R. (2016). Thermal processing of packaged foods (3rd ed.). Springer. doi.org/10.1007/978-3-319-24904-9.
Patashnik, M. (1953). A simplified procedure for thermal process evaluation. Food Technol., 7(1), 1-6.
Simpson, R., Almonacid, S., & Teixeira, A. (2003). Bigelow’s general method revisited: Development of a new calculation technique. J. Food Sci., 68(4), 1324-1333. doi.org/10.1111/j.1365-2621.2003.tb09646.x.
Stumbo, C. R. (1973). Thermobacteriology in food processing (2nd. ed.). New York, NY: Academic Press.
Teixeira, A., Almonacid, S., & Simpson, R. (2006). Keeping botulism out of canned foods. Food Technol., 60(2), Back page.


