6.4: Energy conservation in a Newtonian fluid
- Page ID
- 18069
By assuming that mass and momentum are conserved, we have developed equations for density and flow velocity. To arrive at a closed set of equations, we must also invoke conservation of energy. We’ll do this in a rather roundabout fashion. The discussion of energy conservation leads us to an intuitively appealing summary of the factors affecting the motion and evolution of a fluid parcel which we’ll take some time to explore. It also frustrates our attempt at closure by introducing new variables, necessitating some additional assumptions about the nature of the fluid and the changes that it undergoes. Finally, we arrive at a closed system of equations that we can, in principle, solve to predict fluid behavior in a wide variety of situations.
We can often gain greater understanding of a physical system by identifying its evolution as an exchange of energy among two or more“ reservoirs’’, or kinds of energy. In a Newtonian fluid, energy is exchanged between kinetic, potential and internal forms through various identifiable processes. Recall that a fluid is in fact made of molecules (section 1.2). What we call the flow velocity is really the average velocity of many molecules occupying a small space. Besides this average velocity, each molecule is doing its own complicated dance, whizzing around, spinning, oscillating, and colliding randomly with its neighbors. The kinetic energy of these microscopic motions is manifested macroscopically as the temperature of the fluid. In energetic terms, it is regarded as part of the internal energy. In a compressible flow, squeezing molecules together requires that work be done against intermolecular forces. The result is analogous to the storage of potential energy in a compressed spring, and is treated as part of the internal energy.
6.4.1 Kinetic energy
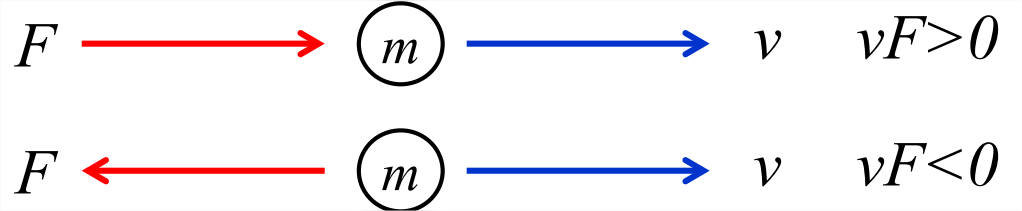
We begin by recalling some basic concepts from solid body mechanics. A solid object of mass m (see Figure \(\PageIndex{1}\)), moving at speed \(v\), has kinetic energy
\[K E=\frac{1}{2} m v^{2}. \nonumber \]
The object also has momentum \(mv\), which changes in time according to Newton’s second law when a force \(F\) is applied:
\[\frac{d}{d t} m v=F.\label{eqn:1} \]
The connection between momentum and kinetic energy is made by multiplying both sides of Equation \(\ref{eqn:1}\) by \(v\):
\[v \frac{d}{d t} m v=\frac{d}{d t} \frac{1}{2} m v^{2}=v F. \nonumber \]
The product \(vF\) is called the rate of working of the force \(F\) upon the object. If \(vF > 0\), i.e., if the force acts in the direction that the object is already moving, it tends to increase the object’s kinetic energy. The opposite is true if the force is opposite to the motion.
The kinetic energy of a fluid parcel is given by
\[K E=\int_{V m} \frac{1}{2} \rho u_{j}^{2} d V. \nonumber \]
The analogue of Newton’s second law is Cauchy’s equation Equation 6.3.18. Multiplying both sides of Equation 6.3.18 by \(uj\), we have
\[\rho u_{j} \frac{D u_{j}}{D t}=\rho u_{j} g_{j}+u_{j} \frac{\partial \tau_{i j}}{\partial x_{i}}.\label{eqn:2} \]
The left-hand side of Equation \(\ref{eqn:2}\) is easily transformed using the product rule of differentiation (omitting the factor \(\rho\) for simplicity):
\[\begin{align}
u_{j} \frac{D u_{j}}{D t} &=u_{j} \frac{\partial}{\partial t} u_{j}+u_{j} u_{i} \frac{\partial}{\partial x_{i}} u_{j} \label{eqn:3}\\
&=\frac{\partial}{\partial t} \frac{1}{2} u_{j}^{2}+u_{i} \frac{\partial}{\partial x_{i}} \frac{1}{2} u_{j}^{2}=\frac{D}{D t}\left(\frac{1}{2} u_{j}^{2}\right)\label{eqn:4}
\end{align} \nonumber \]
Restoring \(\rho\) and integrating over the fluid parcel then gives
\[\int_{V_{m}} \rho u_{j} \frac{D u_{j}}{D t} d V=\int_{V_{m}} \rho \frac{D}{D t}\left(\frac{1}{2} u_{j}^{2}\right) d V=\frac{D}{D t} \int_{V_{m}} \rho \frac{1}{2} u_{j}^{2} d V=\frac{D}{D t} K E, \nonumber \]
where Cauchy’s lemma Equation 6.3.15 has been used for the second step. We therefore have an evolution equation for the kinetic energy of the fluid parcel:
\[\frac{D}{D t} K E=\int_{V_{m}} \rho u_{j} g_{j} d V+\int_{V_{m}} u_{j} \frac{\partial \tau_{i j}}{\partial x_{i}} d V. \nonumber \]
The terms on the right hand side represent the rates of working by gravity and by contact forces, respectively. The contact term is worth a closer look. Using the product rule, we can rewrite its integrand in two parts,
\[u_{j} \frac{\partial \tau_{i j}}{\partial x_{i}}=\frac{\partial}{\partial x_{i}}\left(u_{j} \tau_{i j}\right)-\tau_{i j} \frac{\partial}{\partial x_{i}} u_{j},\label{eqn:5} \]
which we will investigate seperately. The volume integral of the first term can be converted to a surface integral using the generalized divergence theorem (section 4.2.3)
\[\int_{V_{m}} \frac{\partial}{\partial x_{i}}\left(u_{j} \tau_{i j}\right) d V=\oint_{A_{m}} u_{j} \tau_{i j} n_{i} d A, \nonumber \]
where \(\hat{n}\) is the outward normal to the parcel boundary \(A_m\). Noting that \(\tau_{ij}n_i=f_j\), we can write this area integral as
\[\oint_{A_{m}} \vec{u} \cdot \vec{f} d A. \nonumber \]
Analogous in form to Equation \(\ref{eqn:1}\), this is the rate of working by contact forces at the parcel boundary.
The second term in Equation \(\ref{eqn:5}\) is the rate of working by contact forces in the interior of the parcel. The integrand is split into two parts by recalling Equation 5.3.5 , the symmetric-antisymmetric decomposition of the deformation tensor:
\[\frac{\partial u_{j}}{\partial x_{i}}=e_{j i}+\frac{1}{2} r_{j i}=e_{i j}-\frac{1}{2} r_{i j}. \nonumber \]
Therefore
\[-\tau_{i j} \frac{\partial u_{j}}{\partial x_{i}}=-\tau_{i j}\left(e_{i j}-\frac{1}{2} r_{i j}\right)=-e_{i j} \tau_{i j}, \nonumber \]
where the final equality results from the fact that \(\underset{\sim}{r}\) is antisymmetric while \(\underset{\sim}{\tau}\) is symmetric. This term can be further subdivided by substituting Equation 6.3.32:
\[-e_{i j} \tau_{i j}=-e_{i j}\left(-p \delta_{i j}+\lambda \delta_{i j} e_{k k}+2 \mu e_{i j}\right)=p e_{j j}-2 \mu e_{i j} e_{i j}-\lambda e_{k k}^{2} \nonumber \]
The three terms on the right-hand side represent distinct physical processes.
• The first term, \(pe_{jj}\) represents the rate of working by pressure, or the expansion work. If the fluid is expanding, \(e_{jj}>0\), the outward force of pressure accelerates the expansion, increasing kinetic energy, whereas contraction is opposed by pressure.
• The second term is negative definite and is important enough to have its own symbol:
\[-2 \mu e_{i j} e_{i j}=-\rho \varepsilon. \nonumber \]
This term represents the action of ordinary viscosity, which decreases kinetic energy whenever strain is nonzero. This process is called dissipation, and ε is called the kinetic energy dissipation rate.1 It is most commonly written as
\[\varepsilon=2 v e_{i j}^{2}, \nonumber \]
where \(ν = \mu/\rho\) is the kinematic viscosity. Typical values are
\[v=\left\{\begin{array}{ll}
10^{-6} m^{2} s^{-1}, & \text {in water } \\
1.4 \times 10^{-5} m^{2} s^{-1}, & \text {in air. }
\end{array}\right.\label{eqn:6} \]
• The final term represents the action of the second viscosity. The term is negative semidefinite: zero if the divergence is zero, negative if the divergence is nonzero. Therefore, the second viscosity opposes any divergent motion, either expansion or contraction. The second viscosity term is small in most naturally-occurring flows and will be neglected from here on, but it is easily retrieved if needed.
We can now assemble these various terms to make the evolution equation for the kinetic energy of the fluid parcel:
\[\frac{D}{D t} K E=\underbrace{\int_{V_{m}} \rho \vec{u} \cdot \vec{g} d V}_{\text {gravity }}+\underbrace{\oint_{A_{m}} \vec{u} \cdot \vec{f} d A}_{\text {surface contact }}+\underbrace{\int_{V_{m}} p \vec{\nabla} \cdot \vec{u} d V}_{\text {expansion work }}-\underbrace{\int_{V_{m}} \rho \varepsilon d V}_{\text {viscous dissipation }}\label{eqn:7} \]
6.4.2 Mechanical energy
Further insight into the gravity term can be gained by working in gravity-aligned coordinates. The gravity vector is \(\vec{g}=-g\hat{e}^{(z)}\), where \(g\) is taken to be a constant and \(\hat{e}^{(z)}\) defines the vertical direction. We can now write
\[\vec{u} \cdot \vec{g}=-g \vec{u} \cdot \hat{e}^{(z)}=-g w, \nonumber \]
where \(w\) is the vertical component of velocity. Now note that, as a parcel moves, \(w\) is the time derivative of its vertical coordinate:
\[\frac{D z}{D t}=\frac{\partial z}{\partial t}+u \frac{\partial z}{\partial x}+v \frac{\partial z}{\partial y}+w \frac{\partial z}{\partial z}=0+0+0+w. \nonumber \]
Since \(g\) is a constant, we have
\[\vec{u} \cdot \vec{g}=-\frac{D}{D t} g z. \nonumber \]
The gravity term in Equation \(\ref{eqn:7}\) now becomes
\[-\int_{V_{m}} \rho \frac{D}{D t}(g z) d V=-\frac{D}{D t} \int_{V_{m}} \rho g z d V, \nonumber \]
where Equation \(\ref{eqn:6}\) has been used. The volume integral on the right hand side represents the potential energy of the fluid parcel; hence, the gravity term represents an exchange between kinetic and potential energies. We now have an equation for the sum of kinetic and potential energy, called the mechanical energy:
\[\frac{D}{D t} \int_{V_{m}}\left(\frac{1}{2} \rho|\vec{u}|^{2}+\rho g z\right)=\oint_{A_{m}} \vec{u} \cdot \vec{f} d A+\int_{V_{m}} p \vec{\nabla} \cdot \vec{u} d V-\int_{V_{m}} \rho \varepsilon d V.\label{eqn:8} \]
The concept of potential energy is equally valid in other coordinate frames. For the general case, we define \(\phi\) as the specific2 potential energy such that the net potential energy of a fluid parcel is \(PE = \int_{V_m}\rho \phi dV\) and
\[\vec{u} \cdot \vec{g}=-\frac{D}{D t} \Phi, \nonumber \]
so that \(\phi = gz\) in the special case of gravity-aligned coordinates. We can write this as a Lagrangian evolution equation for the potential energy of a fluid parcel:
\[\frac{D}{D t} \int_{V_{m}} \rho \Phi d V=-\int_{V_{m}} \rho \vec{u} \cdot \vec{g} d V.\label{eqn:9} \]
6.4.3 Internal energy and heat
The first law of thermodynamics can be postulated as follows:
The change of energy stored in a physical object equals the work done on the object by its environment plus the heat added.
Before we explore the consequences of this for a fluid parcel, we represent the heat flux through a material as the vector field
\[\vec{q}(\vec{x}, t)=-k \vec{\nabla} T+\vec{q}_{r a d},\label{eqn:10} \]
where the two terms on the right hand side represent conduction and radiation, respectively. The scalar \(k\) is called the thermal conductivity. We define \(\mathscr{I}\) as the internal energy per unit mass, so that \(\rho\mathscr{I}\) is the internal energy per unit volume. We can now write the first law of thermodynamics as:
\[\frac{D}{D t} \int_{V_{m}}\left(\frac{1}{2} \rho|\vec{u}|^{2}+\rho g z+\rho \mathscr{J}\right)=\oint_{A_{m}} \vec{u} \cdot \vec{f} d A-\oint_{A_{m}} \vec{q} \cdot \hat{n} d A.\label{eqn:11} \]
Subtracting Equation \(\ref{eqn:8}\), we obtain an equation for the internal energy of the fluid parcel:
\[\frac{D}{D t} \int_{V_{m}} \rho \mathscr{J} d V=\underbrace{-\oint_{A_{m}} \vec{q} \cdot \hat{n} d A}_{\text {heat input }}-\underbrace{\int_{V_{m}} p \vec{\nabla} \cdot \vec{u} d V}_{\text {loss to expansion }}+\underbrace{\int_{V_{m}} \rho \varepsilon d V}_{\text {viscous heating }}.\label{eqn:12} \]
• The first term represents a gain of internal energy if heat is being absorbed by the parcel and a loss if heat is lost.
• If the parcel is expanding, the second term describes a conversion of the potential energy stored in the intermolecular forces to kinetic energy of expansion, and vice versa if the parcel is contracting.
• The third term is the conversion of kinetic energy to heat via visous dissipation, and is always positive (an expression of the second law of thermodynamics).
6.4.4 Summary
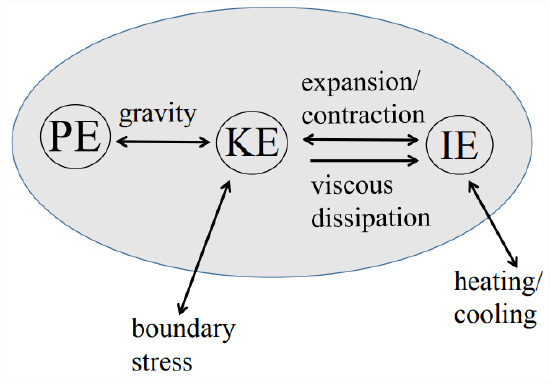
The Lagrangian equations for kinetic, potential and internal energy, collected below, can be summarized in the form of an energy budget diagram (Figure \(\PageIndex{2}\)). The boundary stress represents an interaction with the external environment, as does the heat flux term. These occur only once in the three equations. The remaining terms each occur twice with opposite signs; they therefore represent conversions between energy types within the parcel.
\[\frac{D}{D t} \int_{V_{m}} \frac{1}{2} \rho u_{i}^{2} d V=\underbrace{\int_{V_{m}} \rho \vec{u} \cdot \vec{g} d V}_{\text {gravity }}+\underbrace{\oint_{A_{m}} \vec{u} \cdot \vec{f} d A}_{\text {boundary stress }}+\underbrace{\int_{V_{m}} p \vec{\nabla} \cdot \vec{u} d V}_{\text {expansion }}-\underbrace{\int_{V_{m}} \rho \varepsilon d V}_{\text {dissipation }}.\label{eqn:13} \]
\[\frac{D}{D t} \int_{V_{m}} \rho \Phi d V=\underbrace{-\int_{V_{m}} \rho \vec{u} \cdot \vec{g} d V}_{\text {gravity }}.\label{eqn:14} \]
\[\frac{D}{D t} \int_{V_{m}} \rho \mathscr{I} d V=-\underbrace{\oint_{A_{m}} \vec{q} \cdot \hat{n} d A}_{\text {heat output }}-\underbrace{\int_{V_{m}} p \vec{\nabla} \cdot \vec{u} d V}_{\text {expansion }}+\underbrace{\int_{V_{m}} \rho \varepsilon d V}_{\text {dissipation }}.\label{eqn:15} \]
1This should not be confused with the Levi-Civita tensor \(\underset{\sim}{\epsilon}\) defined in section 3.3.7.
2per unit mass


