2.8: The 0-D DOS - Single Molecules and Quantum Dots Confined in 3-D
( \newcommand{\kernel}{\mathrm{null}\,}\)
The 0-d DOS is a special case because the particle is confined in all directions.
Like a particle in a well with discrete energy levels, we might assume that the density of states in a 0-d might be a series of delta functions at the allowed energy levels. This is indeed true for an isolated 0-d particle.
The lifetime of a charge in an orbital of an isolated particle is infinite. From the uncertainty principle, infinite lifetimes are associated with perfectly discrete energy states in the isolated molecule, i.e. if Δt→∞, ΔE→0.
But when, for example, a molecule is brought in contact with a metal electrode, the electron may eventually escape into the metal. Now, the electron's lifetime on the molecule is finite, and hence the molecule's energy levels should also exhibit a finite width. Thus, molecular energy levels are broadened in a coupled metal-molecule system – the greater the coupling, the greater the broadening of the molecular energy levels.
Let's assume that there are two electrons in the molecular orbital. Let's assume that the lifetime of these electrons on the molecule is τ. Furthermore, let's assume that the decay of the electron probability on the molecule is exponential. Then the time dependence of the electron probability in the molecular orbital is:
|ψ(t)|2=2τexp[−tτ]u(t)
One choice for the corresponding wavefunction is
ψ(t)=√2τexp[−iE0tℏ−t2τ]u(t)
We have included a complex term in the exponent to account for the phase rotation of the electron. The characteristic angular frequency of the phase rotation is E0/ℏ, where E0 is the energy of the molecular orbital in the isolated molecule.
Next we use a Fourier transform to convert from the time to the energy domain. The Fourier transform of ψ(t) gives
A(ω)=√2/τ1/2τ+i(E0/ℏ−ω)
Now from the definition of normalization in angular frequency we require that
12π∫∞−∞|A(ω)|2dω=∫∞−∞g(E)dE
where g(E) is the density of states. Thus,
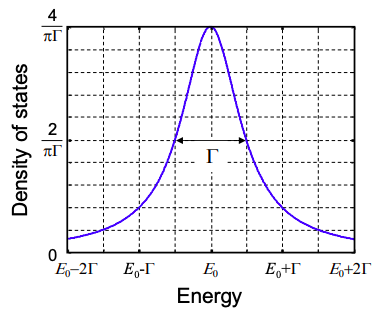
g(E)=12π|A(ω)|2dωdE=2πℏ/2τ(E−E0)2+(ℏ/2τ)2
This function is known as a Lorentzian – it is characteristic of an exponential decay in the time domain; see Figure 2.8.1. The width of the Lorentzian at half its peak value (full width at half maximum, or FWHM) is ℏ/τ. The coupling between the molecule and the contact can be described either by the lifetime of the electron on the molecule τ, or a coupling energy, Γ, equal to the FWHM of the Lorentzian density of states and given by
Γ=ℏ/τ
Thus, as expected, a stronger interaction between a molecule and a contact is correlated with a shorter electron lifetime on the molecule and a broader molecular density of states. In well coupled systems Γ may approach 1 eV, corresponding to an electron lifetime of τ∼4fs.