3.11: JFET

There is a lot more that we could do with field effect devices, but it is probably time to move on to new topics. For one final point, however, we might just look at something called the JFET, or junction field effect transistor. The JFET structure looks like Figure $\PageIndex{1}$. It consists of a piece of p-type silicon, into which two n-type regions have been diffused. However, instead of being both on the same surface, as with a MOSFET, the two regions are opposite one another on either side of the crystal. In cross-section, the JFET looks like Figure $\PageIndex{2}$. We also show the biasing here.

Figure $\PageIndex{1}$: JFET

Figure $\PageIndex{2}$: Biasing a JFET

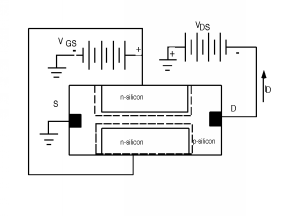
The two n-regions are connected together, and are reverse biased with respect to the p-type substrate. A second battery, $V_{\text{ds}}$, is used to pull current out of the source by applying a negative voltage between the drain and the source. The reverse biased n-p junctions creates a depletion region which extends into the p-type material through which the holes travel as they go from source to drain (a channel?). By adjusting the value of $V_{\text{gs}}$, one can make the depletion region smaller or larger, thus increasing or decreasing the drain current.

The observant student will also note that the polarity of the $V_{\text{ds}}$ battery makes it so that there is more reverse bias across the p-n junctions at the drain end of the channel than at the source end. Thus, a more accurate depiction of the JFET would be what is shown in Figure $\PageIndex{3}$. When the drain/source voltage gets large enough, the two depletion regions will join together, and, just as with the MOSFET, the channel pinches off, as shown in Figure $\PageIndex{4}$.

Figure $\PageIndex{3}$: Depletion region controls current

Figure $\PageIndex{4}$: Pinch-Off

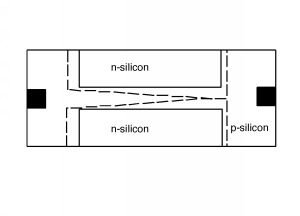
Surprising as it may seem, when you work out the equations which describe how the depletion region extends with $V_{\text{gs}}$ and how the pinch-off mechanism changes $I_{D}$, you end up with behavior, and equations, which are quite similar to those of a depletion-mode MOSFET.

Using JFETs is a little more cumbersome than a normal MOSFET. You must make sure that the gate-substrate junction always remains reverse biased, and since the JFET can only be a depletion-mode device, you have to have a voltage on the gate if you want to turn the transistor off. The JFET does have one advantage over the MOSFET, however. A while back we calculated the value for $C_{\text{ox}}$, the oxide capacitance, and found that it was on the order of $10^{-7} \ \frac{\mathrm{F}}{\mathrm{cm}^2}$. A typical MOSFET gate might be $1 \ \mu \mathrm{m}$ long by $20 \ \mu \mathrm{m}$ wide, and so it would have a gate area of $20 \ \mu \mathrm{m}^{2}$ or $2 \times 10^{-7} \ \mathrm{cm}^{2}$. Thus, the total gate capacitance is only about $10^{-14} \mathrm{~F}$.