Magnetic Domains

The magnetic moments of atoms dictate the magnetic properties of a material. In ferromagnetic materials, long range alignments of magnetic moments, called domains, contain magnetic moments that all point in the same direction. However, if a material were to have all of its magnetic moments pointed in the same direction, this would create a very large external magnetic field. This field is not energetically minimizing as it stores large amounts of magnetostatic energy in the field. Thus, for the system to minimize its internal energy, it must minimize the external field produced. To do this, the material creates different domains within itself to redirect the magnetic field. The regions in-between these domains are known as domain walls. This magnetic domain theory for ferromagnetics was first proposed by Pierre-Ernest Weiss in 1906.

Interactions of a material's exchange interaction, magnetocrystalline anisotropy, and minimization of external magnetic field determine the domain structure of a material.

Exchange Interaction

The exchange interaction is a quantum mechanical effect that causes aligned magnetic moments to be energetically favorable. At a more fundamental level, the exchange interaction in ferromagnetic materials is a consequence of the Pauli Exclusion Principle and electrostatic interactions. The Pauli Exclusion Principle states that fermions, particles with half spin such as electrons, can not occupy the same quantum states. So, for a multi election atom, no two electrons can have the same quantum numbers, n, the principle quantum number, l, the azimuthal quantum number, m_l, the magnetic quantum number, and, m_s, the spin quantum number. For two electrons in a valence shell, where only m_l and m_s may vary, the exchange interaction forces the two electrons to have the same m_s but different m_l, minimizing the electrostatic repulsion of the two electrons.

Electrons in a metal crystal are no longer limited to the atomic orbitals in which they originate. Rather, the electrons are delocalized and form wavefunctions across the whole crystal. However, the Pauli Exclusion Principle still holds, and the electrons each must possess a unique wavefunction. Similarly to the atomic case, neighboring electrons minimize their coulombic repulsion by aligning their spin angular momenta.

Below is the formula for the energy of the exchange interaction between two electrons, where \(J_{ex}\) is the exchange integral while \(s_1\) and \(s_2\) are the spin angular momenta of electrons 1 and 2. As the equation suggests, the exchange energy is dependent on the dot product of the spin angular momenta of the two electrons.

\[E_{ex}=-2J_{ex}\,s_1\cdot s_2 \label{1}\]

Also, since

\[\mu_{spin}=2\mu_B\sqrt{s(s+1)} \label{2}\]

where \(\mu_{spin}\) is the magnetic moment of an atom due to spin angular momentum, \(\mu_{B}\) is the Bohr magneton, and \(s\) is the net spin angular momentum of an atom. Since the magnetic moment of an atom is proportional to the spin angular momentum of an atom and lies in the same direction, the exchange interaction directly affects the magnetic moments within a material.

This is consistent with the above conclusion that the energy is minimized when magnetic moments are parallel. This also suggests that there is an energy maximum when the magnetic moments are anti-parallel, and the smaller the angle between them the lower the energy.

Magnetocrystalline Anisotropy

Due to the low-symmetry nature of crystalline solids, many materials exhibit anisotropy. Anisotropy is the property of being directionally dependent. Magnetocrystalline anisotropy refers to a crystal's property to be more easily magnetized in some directions in comparison to others. For a crystal, the axis easiest to magnetize is known as the easy axis, and the axis hardest to magnetize is known as the hard axis. These easy and hard axes are often fundamental, easy to define, crystallographic direction. For example, the easy axes for bcc iron and fcc nickel are \(<100>\) and \(<111>\) respectively, and their hard axes are \(<111>\) and \(<100>\) respectively.

This propensity to get magnetized in some directions, represents an energetic minimum for magnetic moments to lie in that direction. Thus, forces due to magnetocrystalline anisotropy prefer all magnetic moments pointing in the direction of the easy direction.

Domain Stability

So far, the three main interacting forces causing domain wall formation and domain separation have been discussed: the exchange interaction, magnetocrystalline anisotropy, and minimization of the external magnetic field. Multiple magnetic domains form within one material because it is energetically unfavorable to have one uniform domain, so the magnetic moments split into multiple domains to minimize the internal energy of the system. In figure 1, the entire material is one uniform domain with the magnetic moment in the direction of the materials easy axis. The exchange energy and the magnetocrystalline anisotropy energy are both at absolute minima, however this state also has the highest possible external field energy. Therefore, this state is not at a total energy minimum.

Figure \(\PageIndex{1}\): Ferromagnetic material with one domain, arrowheads representing the direction of the produced external magnetic field, and the large arrow in the rectangle representing the direction of the aligned magnetic moments in the domain.

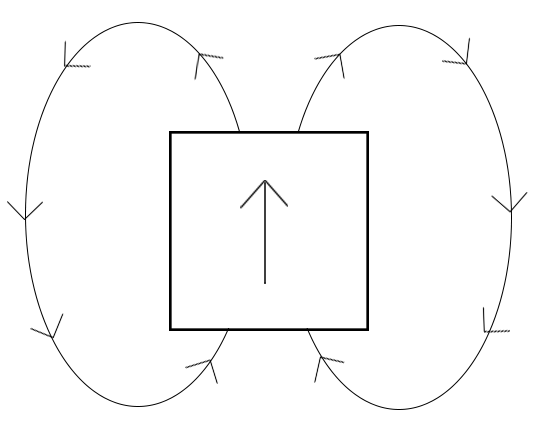
In figure 2, the material is split into two domains, one up and one down. The material now has a much smaller, but still present, external magnetic field. However, the two magnetic domains are anti-parallel with one another, so the exchange interaction between the two domains are at an energy maximum. The two domains are both lying in the direction of the easy axis, so the energy for the anisotropy term is at a minimum.

Figure \(\PageIndex{2}\): Ferromagnetic material with two anti-parallel domains.

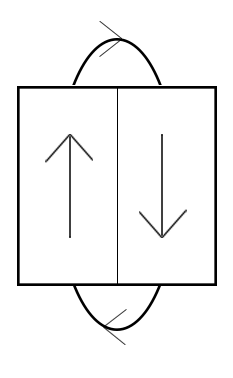
In figure 3, the external field is completely gone, representing an energy minimum in that mode, but there are now domains pointing in directions that are not along the easy axis of the material. However, the domains are not in contact with anti-parallel domains as much, lessening the energy from the exchange interaction compared to figure (2). This state represents the lowest energy of the three states, not just because it minimizes the external magnetic field, but also because it is an intermediate state, balancing the anisotropy and exchange energies.

Figure \(\PageIndex{3}\): Ferromagnetic material with four domain, and no external magnetic field.

Domain Wall Thickness

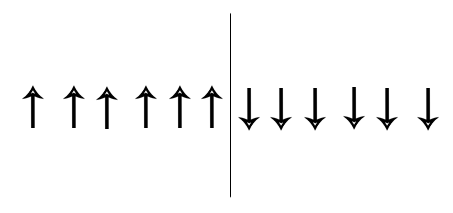
The domain wall is the region between domains, were the magnetic moment transitions from one direction to another. A thin domain wall represents a very quick change in magnetic moment whereas a thick domain wall represents a slow change in magnetic moment. However, when there is an instantaneous change in magnetic moment with no gradual transition between the anti-parallel domains, such as in figure 4 then the neighboring magnetic moments will be anti-parallel. This is the most energetically favorable case for the anisotropy energy term since all moments are aligned on the easy axis, but is the least energetically favorable case for the exchange energy since neighboring magnetic moments are anti-parallel.

Figure \(\PageIndex{4}\): Domain wall of zero thickness

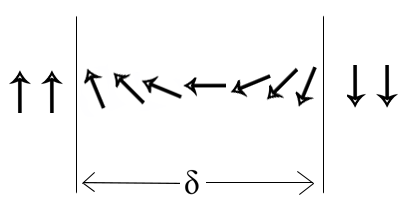
On the other hand, in the case of a very large domain wall, or a very slow transition, the angle between each neighboring moment is very slow, so the exchange energy is at a minimum. However, since the transition is so slow, there are a lot of moments aligned in directions other than the easy axis, so the anisotropy energy is very large. Thus the equilibrium domain wall thickness is some intermediate value that minimizes the combined exchange energy and anisotropy energy.

Figure \(\PageIndex{5}\): Domain wall of thickness \(\delta\)

The potential energy per unit area of the wall, \(U_{wall}\). follows the below relation, where \(E_{ex}\) is the exchange energy (J/atom), \(K\) is the magnetocrystalline energy (J m^-3), \(a\) is the interatomic spacing, and \(\delta\) is the wall thickness. The first term in equation(3) represents the potential energy due to the exchange interaction, and the second term represents the potential energy due to the magnetocrystalline anisotropy.

\[U_{wall}=\dfrac{\pi^2E_{ex}}{2a\delta}+K\delta \label{3}\]

Since the equilibrium wall thickness represents an energy minimum, set the derivative of equation(3) with respect to \(\delta\) equal to zero.

\[\dfrac{dU_{wall}}{d\delta^{\prime}} = \dfrac{-\pi^2E_{ex}}{2a\delta^2} + K = 0 \label{4}\]

Then solve for \(\delta\) in equation (4), to find the equilibrium wall thickness.

\[\delta^{\prime} = \sqrt{\dfrac{\pi^2E_{ex}}{2aK}} \label{5}\]

Also, by substituting equation(5) into equation(3), it can be shown that at this equilibrium thickness, the potential energy contributions from the exchange interaction and anisotropy are equal.

\[U_{ex}=\dfrac{\pi^2E_{ex}}{2a\delta^{\prime}}=\dfrac{\pi^2E_{ex}}{2a}\sqrt{\dfrac{2ak}{\pi^2E_{ex}}}=\sqrt{\dfrac{\pi^2E_{ex}K}{2a}} \label{6}\]

\[U_{K}=K\delta^{\prime}=K\sqrt{\dfrac{\pi^2E_{ex}}{2aK}}=\sqrt{\dfrac{\pi^2E_{ex}K}{2a}} \label{7}\]

This is demonstrated in figure 6 below, where the domain wall energy, exchange energy, and anisotropy energy are plotted as a function of \(\delta\). As the vertical dotted line shows, the minimum in the domain wall energy is the point at where the exchange energy and the anisotropy energy are equal.

Figure \(\PageIndex{6}\): Exchange and Anisotropy energy contributions of the domain wall potential energy as a function of \(\delta\)

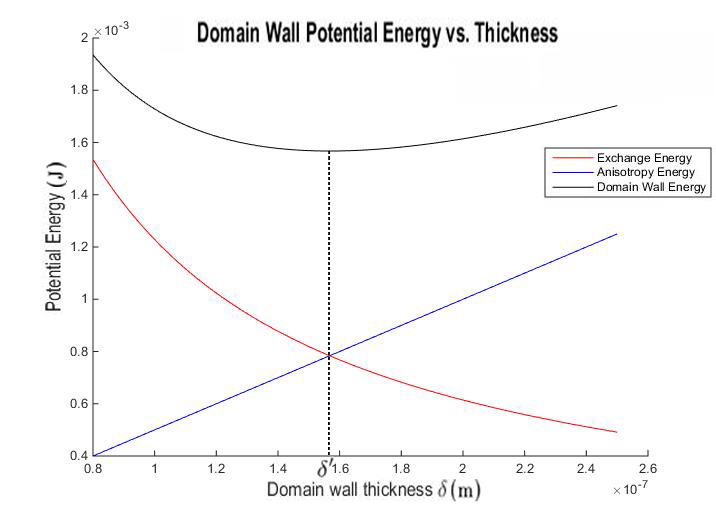
Questions

1. What is the equilibrium domain wall thickness and potential energy for Ni if \(a=3.5\times10^{-10}\,m\), \(E_{ex}=8.712\times10^{-21}\,J\), and \(K=5\times10^{3}\,\frac{J}{m^3}\)?
2. What is the angular dependence of the exchange energy between two neighboring magnetic moments?
3. Ferromagnetic materials have long range alignment of magnetic moments stablized by the exchange interaction, but paramagnetic materials have almost completely randomized magnetic moments. However, ferromagnets only exhibit ferromagnetic responses below a certain temperature, T_c, known as the Curie Temperature, above which they exhibit paramagnetic responses to applied magnetic fields. What causes this shift in properties at higher temperatures?

Answers

1. Use equation (5) to find the domain wall thickness

\[\delta^{\prime} = \sqrt{\dfrac{\pi^2E_{ex}}{2aK}} \label{8}\]

\[\delta^{\prime}= \sqrt{\dfrac{\pi^2(8.712\times10^{-21})}{2(3.5\times10^{-10})(5\times10^{3})}} \label{9}\]

\[\delta^{\prime}=1.56\times10^{-7}m \label{10}\]

Then solving for domain wall energy but substituting equation (10) into equation (3)

\[U_{wall}=\dfrac{\pi^2E_{ex}}{2a\delta^{\prime}}+K\delta^{\prime} \label{11}\]

\[U_{wall}=\dfrac{\pi^2(8.712\times10^{-21})}{2(3.5\times10^{-10})(1.56\times10^{-7})}+(5\times10^{3})(1.56\times10^{-7}) \label{12}\]

\[U_{wall}=0.0016\dfrac{J}{m^{2}} \label{13}\]

2. The formula for the exchange interaction between two spin angular momenta is:

\[E_{ex}=-2J_{ex}\,s_1\cdot s_2 \label{14}\]

Which includes a dot product, so can be expressed as

\[E_{ex} = -2J_{ex}|s_1||s_2|\sin(\theta) \label{15}\]

Where \(J_{ex}\), \(|s_1|\), and \(|s_2|\) are constant in terms of \(\theta\), so

\[E_{ex}\propto\sin(\theta) \label{16}\]

3. The exchange interaction is an energy that wants magnetic moments to be all be aligned in the same direction. However, thermal energy that wants to randomize the system, including the magnetic moments. Thus, they are at odds with each other. By increasing the thermal energy, the thermal energy can overcome the exchange interaction and cause magnetic moments to randomize like a paramagnetic material. This temperature is known as the Curie temperature, \(T_c\) where

\[E_{ex}=-2J_{ex}\,s_1 \cdot s_2\approx k_bT_c \label{17}\]

References

1. Hummel, Rolf E, Electronic Properties of Materials. New York, NY: Springer, 2012.
2. S.O. Kasap, Principles of Electronic Materials and Devices, third edition, New York: McGraw Hill, 2006
3. N.A. Spaldin, Magnetic Materials: Fundamentals and Device Applications, second edition, Cambridge University Press, 2011

Contributors and Attributions

• Matthew Han (University of California, Davis, Material Science and Engineering)