Band Theory of Semiconductors
- Page ID
- 359
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)According to the band theory, semiconductors will actually act as insulators at absolute zero. Above this temperature and yet still staying below the melting point of the solid, the metal would act as a semiconductor.Semiconductors are classified by the fully occupied valence band and unoccupied conduction band. With the small band gap in between these two bands, it takes a certain amount of energy to excite the electrons from the valence to conduction band. Thus it follows that the higher the temperature, the more conductive the solid will be (Figure 1).
Band Energy
As stated previously, continuous bands of energy are formed due to the combinations of molecular orbitals close in energy. Of course, due to the mass amounts of different molecular orbital mixings, bands of varying energy will form. The difference between these band energies is known as the band gap, as indicated in Figure 2.
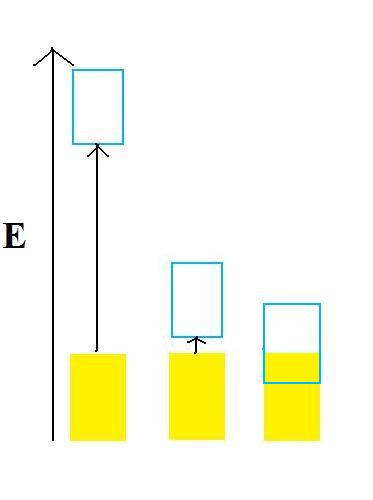
Figure 2. The blue boxes represent the conduction bands while the yellow boxes represent valence bands. The shading of the boxes is indicative of electron density within the band. (a) band energies of an insulator (b) band energy of a semiconductor (c) band energy of a metal
The band theory looks at the jump of electrons across the band gap. In particular, the jump of electrons from their valence band to their conduction band across their Fermi energy level. This "jump" dictates optical and magnetic properties of the solid.
Valence Band
The band of energy where all of the valence electrons reside and are involved in the highest energy molecular orbital.
Conduction Band
The band energy where positive or negative mobile charge carriers exist. Negative mobile charge carriers are simply electrons that had enough energy to escape the valence band and jump to the conduction band. Here, they move freely throughout the crystal lattice and are directly involved in the conductivity of semiconductors. Positive mobile charge carriers are also referred to as holes. Holes refer to the lack of an electron in the conduction band. In other words, a hole refers to the fact that within the band there is a place where an electron can exist (ie. negative mobile charge carrier), and yet the electron ceases to exist at that particular location. Because the electron has the potential to be there and yet isn't there, it is referred to as positive mobile charge carrier.
Fermi Level
This level refers to the highest occupied molecular orbital at absolute zero. It is usually found at the center between the valence and conduction bands. The particles in this state each have their own quantum states and generally do not interact with each other. When the temperature begins to rise above absolute zero, these particles will begin to occupy states above the Fermi level and states below the Fermi level become unoccupied.
Semiconductors
Semiconductors are defined to have conductivity in between an insulator and a conductor. Due to this property, semiconductors are very common in every day electronics since they likely will not short circuit like a conductor. They get their characteristic conductivity from their small band gap. Having a band gap prevents short circuits since the electrons aren't continuously in the conduction band. A small band gap allows for the solid to have a strong enough flow of electrons from the valence to conduction bands in order to have some conductivity.
Electrons in the conduction band become free from the nuclear charge of the atom and thus can move freely around the band. Thus, this free-moving electron is known as a negative charge carrier since having the electron in this band causes electrical conductivity of the solid. When the electron leaves the valence band, the state then becomes a positive charge carrier, or a hole.
Intrinsic Semiconductors
Pure semiconductors in which its properties are solely based off of the material itself. Here, the number of electrons in the conduction band equal the number of holes in the valence band. Theses semiconductors are also known as i-types.
Extrinsic Semiconductors
Impure semiconductors that have been "doped" in order to enhance its conductivity. There are two types of extrinsic semiconductors: p-type and n-type. A "dopant" atom is added to the lattice in order to draw electrons from the valence band. This atom is referred to as an acceptor. As more acceptors are added to the lattice, the number of holes will begin to exceed the number of negative charge carriers, eventually leading to a p-type (positive type) semiconductor. N-type semiconductors have a large number of donors, "dopant" atoms that donate electrons to the conduction band.
Problems
- How does the band gap indicate whether or not your substance is an insulator, semiconductor or conductor?
- What is the purpose of a p-type semiconductor? An n-type?
- What is the purpose of understanding band theory?
Answers
- A very large band gap is indicative of an insulator--since it takes a great deal of energy for the electron to "jump" from the valence band to the conduction band, there will not likely be any conductivity. In conductors (metals) there is zero band gap, therefore the valence and conduction bands overlap. This allows for constant conductivity. Semiconductors thus have a very small band gap, meaning that their conductivity is in between that of an insulator and conductor.
- P-type conductors create an abundance of holes while n-types create an abundance of negatively charged carriers (conduction electrons) for the host material.
- It explains a substance's metallic character (and thus its conductivity).
Contributors and Attributions
- Mary Magsombol
References
- Neamen, Donald (2006). An Introduction to Semiconductor Devices (1st ed.) McGraw-Hill.
- Housecroft, Cathernie E.; Sharpe, Alan G (2008). Inorganic Chemistry (3rd ed.) Pearson Education Limited.

