Fermi level
- Page ID
- 361
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The Fermi Level is the energy level which is occupied by the electron orbital at temperature equals 0 K. The level of occupancy determines the conductivity of different materials. For solid materials such as metals, the orbital occupancy can be calculated by making an approximation based on the crystalline structure. These orbitals, combined with the energy level, determine whether the material is an insulator, semi-conductor, or conductor. The orbitals are categorized according to its energy. The lower energy orbitals combine and form a band called the valence electron band, and the higher energy orbitals combine to form a band called the conduction band. There is a gap between the valence and conduction band called the energy gap; the larger the energy gap, the more energy it is required to transfer the electron from the valence band to the conduction band.
Energy Band Diagram
The diagram below is an example of an energy band diagram. The upper box represents the conduction band, the lower box represents the valence band, and the yellow is the occupancy level of electrons. The conductivity of a material can be determined by the energy diagram. In order to conduct electricity, an electron must make a transition into another state since electrons cannot occupy the same quantum states. When the electron cannot make that transition, it will be not be able to conduct electricity. When the band is completely filled, the closest state an electron to transfer to will be the states in the conduction band, and that would require the electron to jump over the band gap, thus making it more difficult to conduct electricity. With this rule, it is easy to tell the difference between insulator, semi-conductor, and conductors. The energy band on the left side is an insulator because if an electron wants to go into a higher energy state, it will need to jump through that huge energy gap. Since it requires a large amount of energy to move the electron, the material will have a difficult time conducting electricity. The energy band in the middle is a semi-conductor because although the electrons have to jump across the energy gap, the energy gap is small. If an electron wants to make a transition, it will require very little energy since they are all int he same energy band. Thus, for the material in the middle, although it will have difficulty conducting electricity, it is not impossible. The energy band in the right is a conductor. Although the valence band is filled just like the insulator and semi-conductor, the conduction band overlaps the valence band. If an electron wants to make a transition, it will require very little amount of energy. Which means the material on the right can conduct electricity very easily.
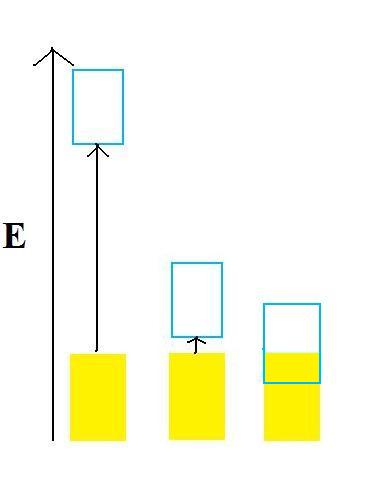
Fermi Level
The electrons that occupies the orbits are described by Fermi-Dirac distribution as the figure below, the distribution takes on the form of:
\[\dfrac{1}{1+\exp[ (E-u)/KT]}\]
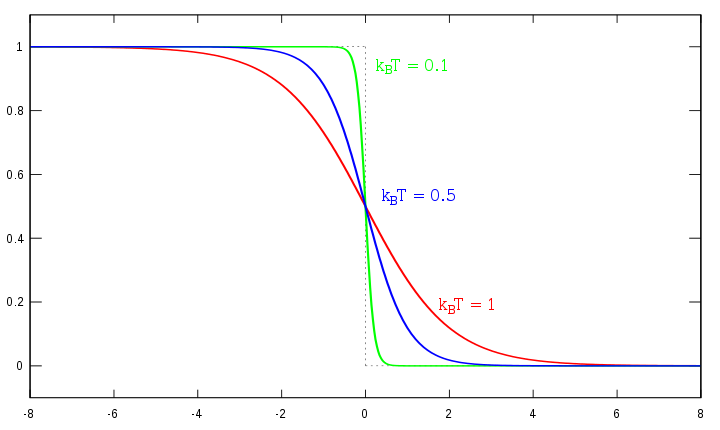
http://upload.wikimedia.org/wikipedi...irac_distr.svg
Where E is the energy of the system, \(u\) is the fermi level, K is the Boltzmann constant, and T is the temperature. The Fermi-Dirac distribution accounts for the population level at different energies. The Fermi level is at \(e/u = 1\) and \(KT = u\). Whenever the system is at the Fermi level, the population n is equal to 1/2. The tail part in the exponential is very important for the conductivity of semi-conductors. If you can bring the Fermi level high enough, then part of the tail will go over to the conduction band. Thus, the electron will have an easier time making a transition to the conduction band and the conductivity will increase. The conductivity can also be affect by factors such as temperature and purity. From the distribution, the temperature has a direct effect on how the energy states are populated. When temperature increases the tail of the exponential gets longer and wider, thus making the conduction band level population more accessible. For Semi-conductor materials, having an access to the conduction band level means it can conduct electricity with energy, which means the conductivity of the material is increased. The purity also affects the Fermi level. Purity defects with atoms that have excess electrons would bring the Fermi level up, and making it easier for electrons to jump into the conduction band.
References
- Kittel, Charles. Introduction to Solid State Physics. Eighth edition. New Jersey: John wiley & Sons, Inc, 2005.
- Griffiths, Davis. Introduction to Quantum Mechanics. Second edition. New Jersey: Pearson Education, Inc, 2005.
- Band energies.jpg
Problems
1. Besides the Fermi Level, what other factor determines the population in different energy levels?
answer: Temperature
2. What is the difference between a semi-conductor and an insulator?
answer: A semi-conductor has a smaller band gap and therefore, while more difficulty than a conductor, is able to conduct electricity if you put in enough energy.
3. What does the Fermi level determines?
answer: The Fermi level determines several factors. It determines the population at different energy levels. It also determines how easily can the material conductor electricity. As your Fermi level approaches your conduction band energy, it will be easier for the electrons from the valence band to travel to the conduction band.

